基于负熵的旋转机械盲信号处理
毋文峰 陈小虎 苏勋家 姚春江 王旭平
第二炮兵工程学院,西安,710025
基于负熵的旋转机械盲信号处理
毋文峰 陈小虎 苏勋家 姚春江 王旭平
第二炮兵工程学院,西安,710025
针对机械设备盲信号处理实践中,机械源信号数目大于多通道观测数目的欠定盲信号处理问题,将非高斯性的度量指标——负熵和经验模式分解引入机械设备的故障特征提取,提出基于负熵的旋转机械盲信号处理方法,从而解决欠定的单通道机械盲信号处理问题。首先将机械设备的单通道观测信号经验模式分解,得到本征模函数,然后计算本征模函数的负熵值,并将负熵值依序组成负熵基特征向量,最后采用最小二乘支持向量机进行机械设备的模式判别和故障诊断。液压齿轮泵的盲信号处理试验表明,该方法的故障识别率达到了93%以上,表明该方法是可以应用于机械盲信号处理实践的。
盲信号处理;负熵;经验模式分解;最小二乘支持向量机
0 引言
盲源分离(blind source separation,BSS)和独立成分分析(independent component analysis,ICA)为机械设备故障诊断提供了一种全新的思路,并已在机械故障诊断中取得了初步的应用。在国内,胥永刚等[1]论证了机械振动信号盲源分离的可行性,并探讨了基于独立成分分析的机械故障信息提取方法;李力等[2]论证了自相关预处理可以使独立成分分析更有效地提取机器的状态特征;陈长征等[3]和陈仲生等[4]则研究了盲源分离和独立成分分析在齿轮箱特征提取与故障诊断中的应用;钟振茂等[5]还研究了基于盲源分离的机械声频故障诊断技术。在国外,Ypma等[6]研究了旋转机械源的盲分离技术;Gelle等[7]研究了基于盲源分离技术的旋转机械振动诊断技术和声频诊断技术。但是,目前大多数机械盲信号处理和诊断方法是基于源信号的盲分离,即首先对多通道机械故障信号进行机械故障源信号的提取和分离,之后针对提取和分离的源信号,再应用不同的故障特征提取和诊断方法进行诊断[1-7]。这样,一方面使得机械故障特征提取和诊断的计算量增加,难以实现机械设备的在线诊断;另一方面,盲源分离算法的性能也直接影响了故障特征提取和诊断的准确度。
在机械设备盲信号处理中,信号的非高斯性至关重要,可以说,非高斯的就是独立的,如果没有非高斯性,ICA估计根本无法实现。负熵是非高斯性的一个可操作的鲁棒度量指标,直接反映了机械信号的动态信息特征,在统计意义上,它是随机变量独立性的自然测度。借助负熵,有可能捕捉到不同故障模式机械信号的动态信息特征,因此负熵在ICA和其相关领域被广泛地用作非高斯性的度量[8-10]。此外,在机械设备的盲信号处理和诊断实践中,很多时候机械故障源数目大于其多通道观测数目,即欠定盲信号处理是机械盲信号处理和诊断的一个重要课题。为了解决这些问题,同时为了避免源信号盲分离对于机械故障特征提取和诊断的影响,本文将ICA算法的非高斯性度量准则——负熵引入机械故障特征的提取和诊断中,提出基于负熵的旋转机械盲信号处理方法,并借助经验模式分解(empirical mode decomposition,EMD)的自适应分解能力和最小二乘支持向量机(least squares support vector machine,LS-SVM)的模式识别能力,试验研究负熵基故障特征提取方法在单通道旋转机械盲信号处理和诊断中的应用。
1 基本概念和理论
1.1 负熵
负熵[8-9]是微分熵的一种标准化版本,符号为J,定义为
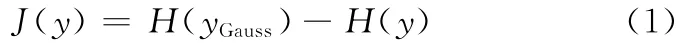
其中,yGauss是与随机变量y具有相同协方差矩阵的高斯随机变量。由此可知,负熵总是非负的,当且仅当y具有高斯分布时其值为零。负熵具有严格的统计理论背景,如果仅考虑其统计效能,那么负熵在一定程度上可以说是非高斯性的最优估计。
在计算中,负熵表示为非多项式函数的加权和[9]:

其中,k1和k2是正常数,yGauss是与y具有相同方差(为1)的零均值高斯变量,y也具有零均值单位方差(标准化)。F1是奇函数,表现随机变量的非对称性,F2是偶函数,表现随机变量在原点左右的双峰性。如果随机变量y对称分布,则式(2)第一项为零,负熵表示为
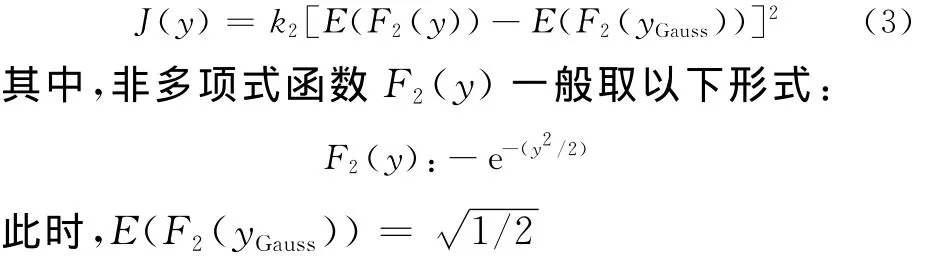
1.2 经验模式分解
经验模式分解是由美国国家宇航局的Huang等[11]提出的。EMD可以将非线性、非平稳信号自适应地分解成为一系列线性、平稳的本征模函数(intrinsic mode function,IMF)信号。本征模函数信号是近似单频率成分的信号,即在每个时刻,IMF信号只有一个频率成分。
EMD的 “筛分”过程见文献[11]。一般,IMF是信号的一种完备的、自适应的、基本正交的表达,但是,在EMD应用中,由于端点效应、曲线拟合等影响,EMD将会产生虚假的伪IMF,尤其对于低频成分来说,情况更加严重。可采用基于相关系数的方法将伪IMF剔除[12]。
1.3 最小二乘支持向量机
支 持 向 量 机 (support vector machine,SVM)[13]是根据统计学习理论中的VC维理论和结构风险最小化原则提出的,是一个凸二次优化问题,能够保证找到的极值解就是全局最优解。但是,SVM的训练是一个有约束的二次规划问题,并且约束数目等于样本容量,这一点使得其训练时间比较长。为了提高SVM的训练效率,Suykens等[14]在SVM的目标函数中增加误差平方和项,提出了最小二乘支持向量机。LS-SVM与SVM的主要区别在于优化的目标函数不同,并以等式约束代替不等式约束,因此LS-SVM的最优化问题是一个等式约束的凸二次规划问题,仅仅相当于解一个线性方程组。因此本文采用LS-SVM实现机械设备的模式识别和故障诊断。最小二乘支持向量机的算法步骤见文献[14]。
2 基于负熵的旋转机械盲信号处理
在机械设备的盲信号处理和诊断实践中,机械故障源数目大于其多通道观测数目的欠定盲信号处理是机械盲信号处理和诊断的一个重要课题,也是一个难点和热点。在以往的机械盲信号处理方法中,大多数是采用基于机械多通道观测信号的盲分离,但盲源分离过程会影响机械故障特征提取的准确性,而且在欠定条件下,盲源分离算法还不成熟。
为了充分利用盲分离理论和算法在处理机械设备多故障中的优势,同时又为了避免盲分离过程对于机械故障特征提取的影响,一个直接的想法是将独立成分分析的计算准则——负熵引入机械设备的故障特征提取。但是,在机械故障源数目大于其多通道观测数目,尤其仅有单通道观测信号的欠定条件下,机械观测信号提供的信息量很有限,因此有必要拓展和挖掘隐藏在机械信号内部的状态信息,以便进一步提取其低维特征向量,而EMD的自适应分解能力正好解决了这个难题。最后,在提取的机械设备故障特征向量的基础上,利用LS-SVM良好的模式识别能力实现机械设备的状态识别和故障诊断。综上所述,基于负熵的旋转机械盲信号处理方法的过程如图1所示。
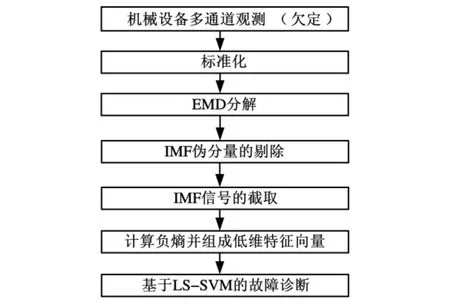
图1 基于负熵的旋转机械盲信号处理方法
由图1可知,该过程的步骤如下(以单通道机械观测信号y为例):
(1)标准化机械设备不同模式类的单通道观测信号yl,使得E(yl)=0,σyl=1,其中,yl代表模式类l的单通道观测信号;
(2)将不同模式类的标准化单通道观测信号yl进行EMD分解,并基于相关系数法,剔除伪IMF分量,得到对应的Nl个IMF信号IMFl={c1,c2,…,cNl};

(6)同样方法,得到不同模式类的低维特征向量;
(7)根据得到的不同模式类的低维特征向量,采用LS-SVM实现机械设备的模式识别和故障诊断。
当机械设备的多通道观测数为Ml(Ml>1),即不止一个通道时,可以依据单通道的方法分别计算不同通道Ml的NMl个负熵值,并将Ml个通道的负熵值联合组成模式类l的低维特征向量。
3 试验研究
液压齿轮泵是一个典型的旋转机械设备,而且它的工作介质是封闭的油液,故其故障源复杂,一般的故障特征提取策略难以有效地提取其低维特征向量,机械设备盲信号处理方法为此提供了一个很好的解决方案。在此,针对基于负熵的旋转机械盲信号处理方法在齿轮泵中的应用进行试验研究。
这里取CB-Kp63型液压齿轮泵壳振动的单通道观测数据,其中,泵壳振动数据由加速度传感器1采集,如图2所示,齿轮泵轴转速为定速1480r/min。

图2 CB-Kp63齿轮泵加速度传感器设置
这里取齿轮泵的正常状态、齿面磨损和轴承故障等3个模式类;采样策略为整周期采样,每个模式均包含64个数据段,每段1024个采样点。图3为齿轮泵不同模式类的时域信号波形。
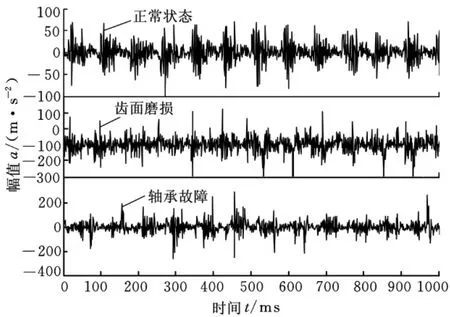
图3 齿轮泵不同模式类的时域信号波形
应用基于负熵的机械故障特征提取方法,由每个模式类的每一段数据得到一个8维的负熵基特征向量,图4a为负熵基特征向量的空间分布(为了便于直观观察不同模式类负熵基特征向量的空间分布,图4a仅仅描绘了其中第1维和第2维的两维负熵基特征向量)。作为对比,在图4b中描绘了不同模式类原始观测数据的散度情况。
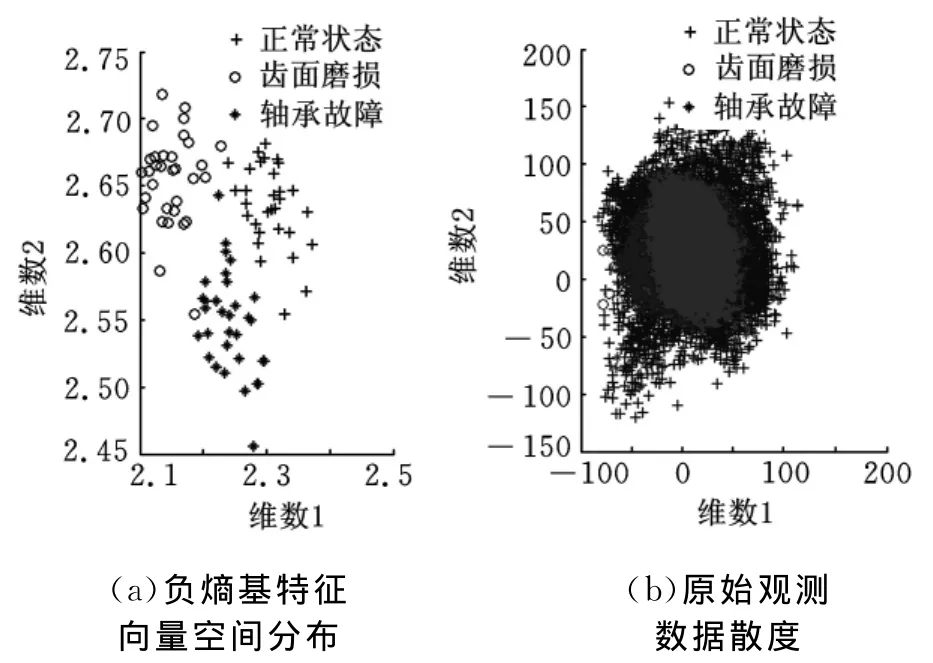
图4 原始观测数据散度和负熵基特征向量空间分布
由图4可见,液压齿轮泵不同模式类的原始观测数据混叠十分严重,难以区分;而负熵基特征向量则呈现出明显的聚类划分特征。由此可见,基于负熵的机械故障特征提取方法能够有效地提取齿轮泵壳振动信号的低维特征向量。
在提取的负熵基特征向量的基础上,进一步采用LS-SVM实现液压齿轮泵的状态识别和故障诊断。由于齿轮泵工作模式包括正常状态、齿面磨损和轴承故障3种状态,属于多类分类问题,因此这里采取一类对余类的多类分类机。
首先训练第一个LS-SVM,它实现齿面磨损故障和其他类的划分。其中,核函数取高斯径向基函数“RBF_kernel”;训练样本由齿面磨损故障类的前32组、轴承故障类的前16组和正常状态的前16组样本组成,共64组训练样本数据。
其次训练第二个LS-SVM,它实现轴承故障和正常状态的划分。同样,核函数取 “RBF_kernel”;而训练样本由轴承故障类的前32组和正常状态的前32组样本组成,共64组训练样本数据。
在多类支持向量机训练完毕之后,分别取齿轮泵3种模式的后32组样本组成测试样本,并测试多分类LS-SVM的分类能力。测试结果如表1所示。
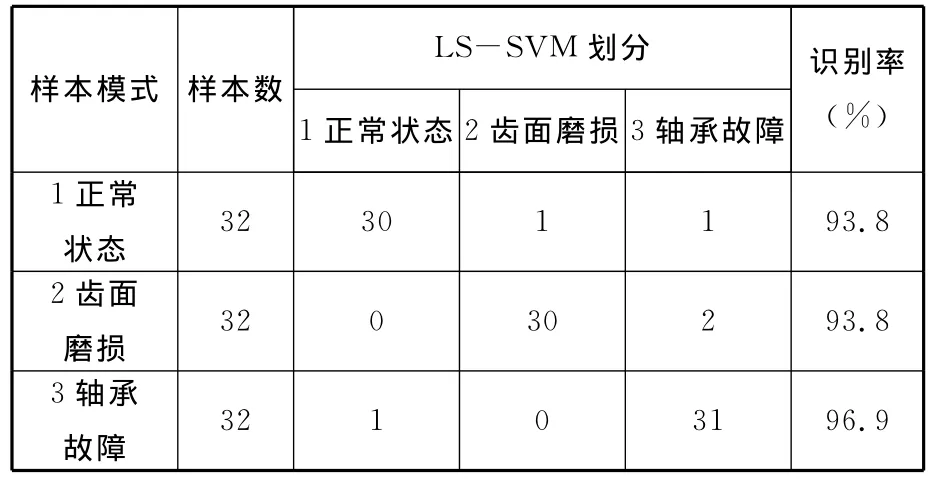
表1 CB-Kp63齿轮泵LS-SVM测试结果
由表1可见,基于负熵的旋转机械盲信号处理和诊断方法很好地实现了液压齿轮泵不同模式类的划分。而且,从表1中可以看出:①基于负熵的旋转机械盲信号处理和诊断方法的故障诊断率比较高,可以达到93%以上,这对于故障源复杂、故障点隐蔽的液压齿轮泵来说,是一个值得研究和应用的方法;②CB-Kp63齿轮泵的LS-SVM诊断结果可以反映出,EMD能够充分挖掘隐藏在机械观测信号内部的深层状态信息,而且机械设备单通道观测信号的IMF负熵值能够正确表征机械设备的工作状态。
4 结论
(1)基于负熵的旋转机械盲信号处理和诊断方法避免了盲分离算法对于故障特征提取的影响,并且减小了计算量,提高了诊断效率。
(2)液压齿轮泵试验表明,在机械故障源数目大于观测信号数目的欠定条件下,基于负熵的旋转机械盲信号处理和诊断方法能够正确解决机械设备的故障特征提取和诊断问题,表明该方法是可以应用于机械设备故障诊断实践的。
[1] 胥永刚,李强,王正英,等.基于独立分量分析的机械故障信息提取[J].天津大学学报,2006,39(9):1066-1071.
[2] 李力,屈梁生.应用独立分量分析提取机器的状态特征[J].西安交通大学学报,2003,37(1):44-47.
[3] 陈长征,程锦生,韩丽娅,等.基于盲源分离的齿轮箱状态检测与故障诊断[J].沈阳工业大学学报,2008,30(4):444-448.
[4] 陈仲生,杨拥民,沈国际.独立分量分析在直升机齿轮箱故障早期诊断中的应用[J].机械科学与技术,2004,23(4):481-483.
[5] 钟振茂,陈进,钟平.盲源分离技术用于机械故障诊断的研究初探[J].机械科学与技术,2002,21(2):282-284.
[6] Ypma A,Leshem A,Duin RPW.Blind Separation of Rotating Machine Sources:Bilinear Forms and Convolutive Mixtures[J].Neuro-computing,2002,49(4):349-368.
[7] Gelle G,Colas M,Delaunay G.Blind Source Separation Applied to Rotating Machines Monitoring by Acoustical and Vibrations Analysis[J].Mechanical System and Signal Processing,2000,14(3):427-442.
[8] Hyvarinen A,Oja E.Independent Component Analysis:Algorithms and Applications[J].Neural Networks,2000,13(4/5):411-430.
[9] Hyvarinen A,Karhunen J,Oja E.Independent Com-ponent Analysis[M].New York:John Wiley &Sons.,Inc.,2001.
[10] 李舜酩,雷衍斌.基于负熵的转子混叠振动信号盲识别[J].中国机械工程,2009,20(4):437-441.
[11] Huang N E,Shen Z,Long S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis[J].Proceedings of the Royal of London Series A,1998,454:903-995.
[12] 于德介,程军圣,杨宇.机械故障诊断的Hilbert-Huang变换方法[M].北京:科学出版社,2006.
[13] Cortes C,Vapnik V.Support Vector Networks[J].Machine Learning,1995,20(2):273-297.
[14] Suykens J A K,Vandewalle J.Least Squares Support Vector Machine Classifiers[J].Neural Processing Letters (S1370-4621),1999,9(3):293-300.
Blind Signal Processing Based on Negentropy for Rotating Machines
Wu Wenfeng Chen Xiaohu Su Xunjia Yao Chunjiang Wang Xuping
The Second Artillery Engineering College,Xi’an,710025
In blind signal processing of mechanical equipment,it is common that mechanical source number is more than that of multi-channel observation signals.This was called underdetermined blind signal processing.Then negentropy and empirical mode decomposition(EMD)was introduced into feature abstraction of mechanical equipment to deal with their single channel blind signal processing.This algorithm was composed of three steps.Step 1was to decompose single channel mechanical observation signals with empirical mode decomposition and get intrinsic mode functions(IMFs).Step 2 was to compute negentropy values of IMFs and form a negentropy eigenvector according to IMFs sequence.Step 3was to recognize different working patterns and diagnose different faults with LSSVM.Its applications in blind signal processing of hydraulic gear pumps show that,its fault diagnosis rate is up to 93%on the whole.This indicates that this algorithm can be applied to mechanical blind signal processing.
blind signal processing;negentropy;empirical mode decomposition;least square support vector machine(LS-SVM)
TH165.3;TP391.4
1004—132X(2011)10—1193—05
2010—07—14
总装备部预研重点基金资助项目
(编辑 袁兴玲)
毋文峰,男,1978年生。第二炮兵工程学院五系博士研究生。主要研究方向为机械设备故障诊断和智能信号处理。发表论文10篇。陈小虎,男,1972年生。第二炮兵工程学院五系副教授。苏勋家,男,1965年生。第二炮兵工程学院五系教授、博士研究生导师。姚春江,男,1979年生。第二炮兵工程学院五系讲师。王旭平,男,1978年生。第二炮兵工程学院五系讲师。

