基于链传动啮合特性的正时链参数设计
李宝林 唐 力 初晓亮 范 帅
中国矿业大学,徐州,221116
基于链传动啮合特性的正时链参数设计
李宝林 唐 力 初晓亮 范 帅
中国矿业大学,徐州,221116
用几何法及虚位移原理分析了不同结构参数及不同初始相位角下链的传递特性,并分析了链轮中心距对从动轮角速度变化和链传动不均系数的影响规律,绘制了链传动初始相位几何特征参数对从动轮角速度和链传动不均系数影响的变化趋势。依此分析在其他参数确定的情况下,通过设计阻尼器导板压入量与曲率半径等参数来改变啮合特性以达到最小的角速度波动及变化参量,提出了高速链设计的辅助公式及验证约束方程,为发动机正时链系统设计提供思路和方法。
链传动特性;正时链;减振导板;链传动不均系数
0 引言
链啮合冲击是采用正时链系统的发动机的噪声源之一。由于链条与链轮的啮合属非共轭啮合,链条中心线的位置存在着周期性的变化,每个链节与链轮的接触及脱离是在瞬间完成的[1],因此链传动具有独特的动力传递特性,链条在与链轮啮合的过程中呈现交替相切和相割的多边形传动效应并产生冲击力,也就出现了传递过程中相应的转动半径的变特性,导致了链传动过程中从动轮转动角速度的波动性[2]。由于多边形链轮在工作中是近似挠性传递的,因此导致了传递过程中从动轮角速度的变化。结构参数的不同会产生不同的从动轮转动角速度波动曲线和导致链传动不均系数Kk的变化。在汽车发动机上的正时链会出现链条啮合冲击噪声[3],并导致发动机使用性能的降低和寿命的缩短。
通常发动机转速为4800r/min,特殊发动机转速可达15 000r/min[4],因此发动机正时链设计时,应尽可能减小传动的不均系数Kk,减小链条啮合时的冲击,提高发动机的使用性能。多体动力学软件ADAMS中的子模块Engine Chain比较适用于发动机正时系统的设计,可进行阻尼系数等变量的模拟设计,根据不同参量的变化演示不同参数结果,但参数初始的设计和选择仍需要通过基本理论确认才能更好地符合软件内的专家系统。国内正时链自行设计尚处于探索阶段,对于参数的选择和确定尚无依据可循,减振器导板参数设计、张紧器结构确定多来自对国外同类机型的仿制,正时链设计还缺少指导性的设计方法。
1 链传动的基本特性
传统的链传动运动分析中,根据从动轮在传动过程中半径的变化,得到从动轮运动方程:
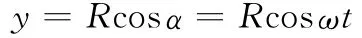
式中,α为初始相位角;R为回转半径。
啮合点位置(以初始相位角α来衡量)的周期变化范围为[-φ/2,φ/2],从动轮瞬时转速ω2在0~φ范围内呈余弦函数规律变化。其中,φ为节距角(弦节距所对应的圆心角),φ=360°/z;z为链轮齿数。
实际上链传动过程中链轮的齿数、中心距及链节长度间的关系都会影响到从动轮角速度的波动特性。在不考虑转速、链条质量、振动等因素的影响[5],传动比i=z1/z2≠1,即主从链轮半径不同(r1≠r2)的情况下,分析不同中心距a0时的链传动特性。正时链系统的基本参数一旦确定,正时链系统的传动特性也随之确定。
单级链传动结构示意图见图1,r1<r2,初始位置时的啮合点为m、n,m点与主动轮圆心O1的连线与铅垂线的初始夹角为α。可以看到,不同的初始角位置有着不同的中心距:
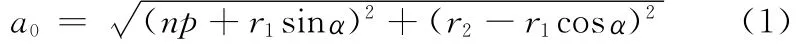
式中,n为对应链轮中心距链节的倍数;p为链节长度。
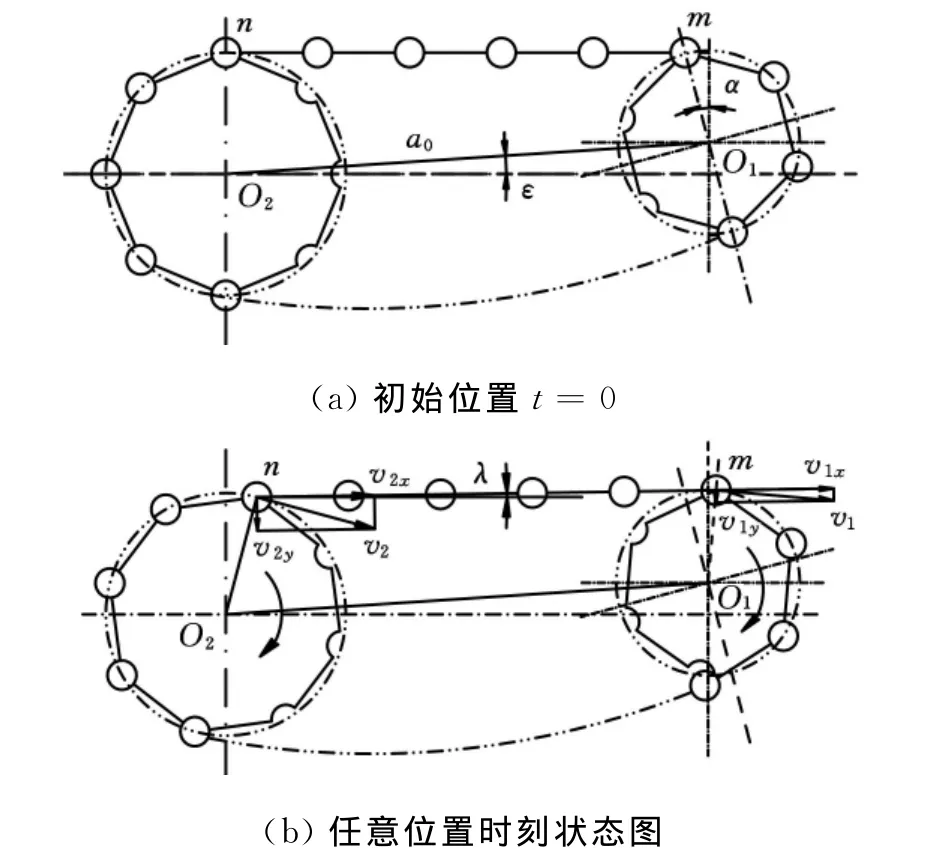
图1 单级链传动结构分析示意图
设定初始变量为α,变化范围为0~φ,为便于分析,中心距也可以表示为:a0=pn+x,x为参数变量,取值范围为0~p。
不考虑啮合点之间的链节振动和弹性变形等因素的影响[6],依据平面运动学虚位移原理分析[7],可得到啮合点m、n处的链传动方程参量。
(1)主动轮啮合点m的水平与垂直方向速度分量:
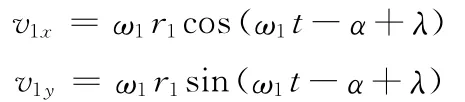
(2)从动轮啮合点n的水平与垂直方向速度分量:


1.1 相同参数链轮的传递特性
(1)当中心距a0=np时,状态如图2a所示。传动比i=z1/z2=1,即r1=r2,n为整数时,初始情况下的α、β、δ、λ均为0°,则可得到:

这种传动在链传动过程中,角速度没有变化,是理想的“同步传动”,但实际传动中链条啮合点在回转半径的交替变化过程中会发生速度的波动[8]与链条的振动[9]。通过振动分析后可以看到,这种传动用于低速、大扭矩、近距离情况下比较理想,但链传动中的啮合冲击和噪声依然存在[10]。
(2)当中心距a0=np+x,0<x<p,x≠0.5p时,状态如图2b所示。其他参数不变时,传动比i=z1/z2=1,r1=r2=r,主动轮初始相位角为α,变量λ≠0°,由式(3)可得
这种传动在传递过程中从动轮角速度ω2是时间t的变量,随着初始角α的变化而有不同值。由式(5)可得从动轮角速度ω2的变化趋势,链传动不均系数Kk随着α值的增大而增大。
(3)当中心距a0= (n+0.5)p时,状态如图2c所示。其他参数不变,传动比i=z1/z2=1,r1=r2,x=0.5p时,主动轮初始相位角为α=φ/2,变量λ≠0°,则有

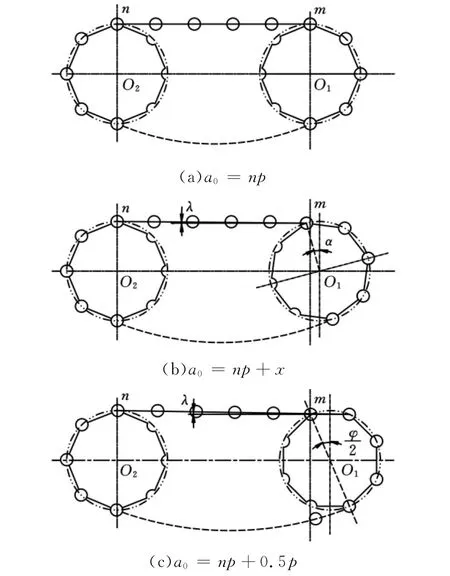
图2 相同参数链轮不同中心距状态分析图
1.2 不同链轮尺寸的传递特性
链轮直径的不同,即r1≠r2,也会影响从动轮角速度ω2的瞬时值和链传动不均系数Kk,如图3所示。
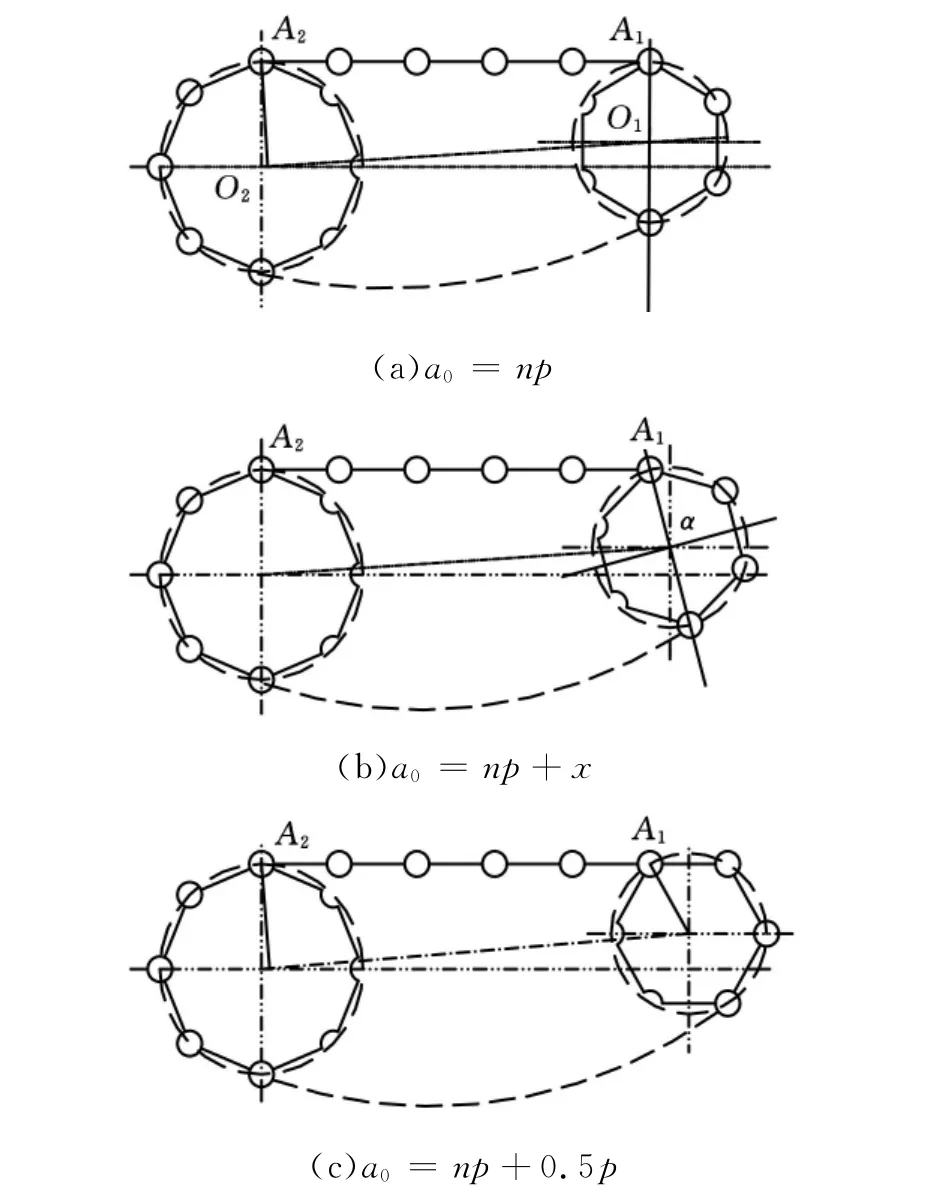
图3 不同参数链轮不同中心距状态分析图
(1)取初始状态主动轮与从动轮的啮合点都处于最高的水平线上,如图3a所示,且啮合点与中心连线都处于垂直状态,即α=0°。则初始位置的中心距为

依据式(4)、式(5)分析,得到不同初始相位角α对ω2的影响曲线,如图4所示。
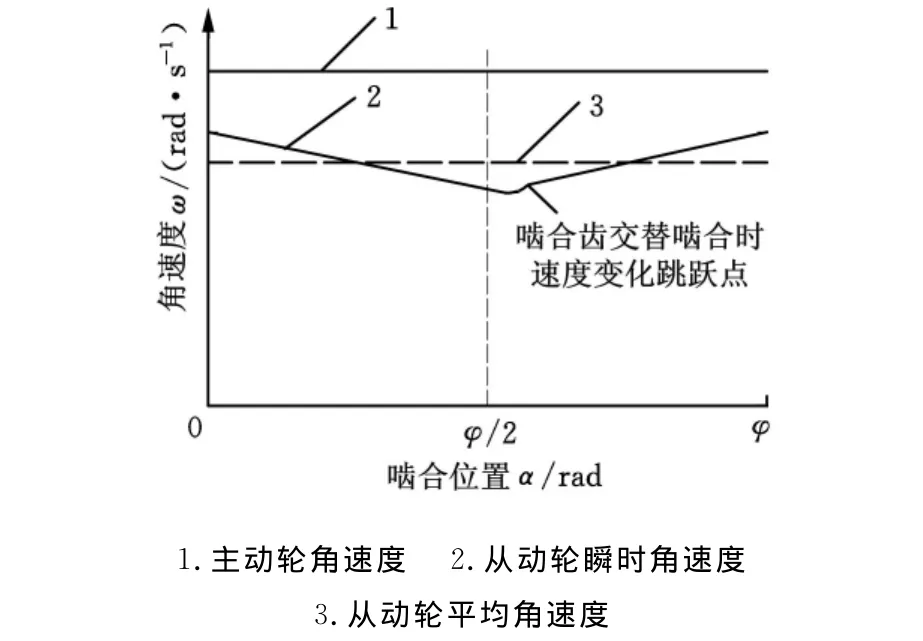
图4 不同初始相位时的ω2变化
(2)当中心距为任意值时,如图3b所示,此时主动轮初始相位角为α,中心距a0为式(1)参数。在该状况下的传递过程中,从动轮角速度ω2是时间t的变量,随着初始角α的变化而有不同值。从上述分析及图3中可以看到,在其他参数确定后,初始相位角α在一定程度上影响着从动轮的传递性能。当两轮的直径确定时,只有当(β-α+λ)与(δ+λ)接近时,从动轮的角速度ω2和不均系数Kk才最小。
(3)当啮合点处于最高点且主动轮的两个啮合点都处于最高位置时,状态如图3c所示,有:
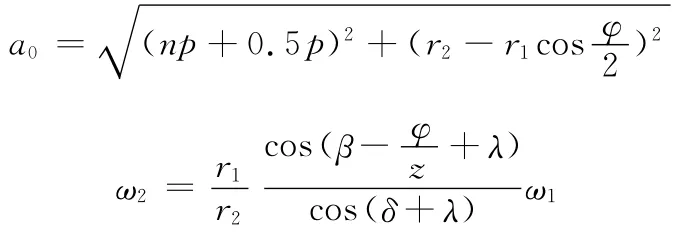
这时的从动轮角速度ω2和不均系数Kk的值最大。依据该公式及式(3)、式(4)分析不同初始相位角α对ω2和Kk的影响,并绘制瞬时从动轮角速度ω2的变化曲线,得到主动轮与从动轮瞬时角速度变化曲线,如图4所示。
1.3 链传动不均系数的影响因素
在链传动设计中,链节距p、中心距a0、链轮齿数z、主动轮或从动轮与两啮合点连线之间的夹角λ都对传动的不均系数产生影响。
(1)两啮合点与两圆心的夹角ε对从动轮的ω2没有显著影响,它只是结构设计上的参数,由链轮的直径和中心距决定,是传动分析时的参照量。
(2)影响不均系数Kk的另一个因素是中心距a0,中心距大比中心距小的效果更好,即中心距增大时,ω2与Kk变化的相对波动减小,这个值也是根据链轮的结构确定的。
(3)在其他参数确定后,夹角λ对ω2与Kk的影响及振动的影响最为显著。当λ=0°时,ω2和Kk的波动和变化最小,同时振动也最弱。
(4)分析图4可以验证,p越小其连杆效应越弱;中心距a0相对较大时,链条紧边的振动角度变化及啮合的波动相对较小。
可以看到,当其他参数不变,夹角λ=0°时,ω2的波动与Kk的变化最小,也就是近似于“同步传动”的“同相位”传动,此种传动中,结构参数的主要特征是中心距与链轮结构之间的关系符合式(8)的表达。
设计过程中,由于结构参数的限制,中心距通常不能改变,且链条传递功率限制了链条的参数(型号、节距、排数、传动比及齿数),所以在链传动系统设计中需依据减振器或阻尼器导板弧度及压入量调整啮合参数以使波动系数Kk最小。
2 发动机正时链设计中参数的确定
2.1 链传动的几何特征与约束
在设计正时链系统时,两轴中心距a0和两驱动轮半径r1、r2不一定能够完全满足式(8)中的参数要求,因此在设计阻尼器导板的圆弧曲率与压入量参数时需达到“同相位传动”的条件。
链传动设计中,当初始条件r1、r2及中心距a0参数都已确定时,如果采用直边传动可能会出现较大的波动系数Kk,因此在设计阻尼器的圆弧曲率半径和适当的压入量Δ时,需保证最佳的设计效果以达到最小的波动系数Kk。
设计路线如下:
(1)由于发动机正时链系统工作转速比较高,故工作的紧边需有起到消除振动作用[11]的阻尼器减振导板。图5a结构中没有阻尼器的传动。如果两个啮合点都可以处于最高的位置,即理想的“同相位传动”状况下,可加直板的阻尼器减振导板;如果啮合点达不到理想的传动初相位角,则需设计一个一定压入量的弧状减振阻尼器导板,如图5b所示。
(2)导板弧度设计依据压入量Δ来确定,在使弧度最大的同时,保证两啮合点的法线通过各自链轮中心,以达到“同相位传动”效果。压入量过大会导致链条与导板的磨损,后期偏离最佳传动效果,较小的压入量可保证不会出现因导板磨损后而导致的啮合较大的变化。导板表面的耐磨材料通常采用尼龙制品,其特点是在有润滑状态下摩擦因数小,耐磨性优于橡胶材料。
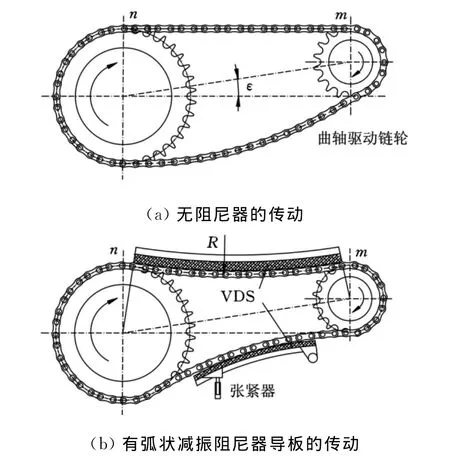
图5 链传动参数设计
(3)导板的圆弧可采用单一圆弧也可根据需要采用分段圆弧设计,但其设计后要进行实际安装并测试其参数[12]。
采用单一圆弧曲线的设计见图6。已知中心距a0和两驱动轮半径r1、r2,简化后几何图的啮合点为m、n,虚拟圆心O3,具体计算可采用如下步骤。
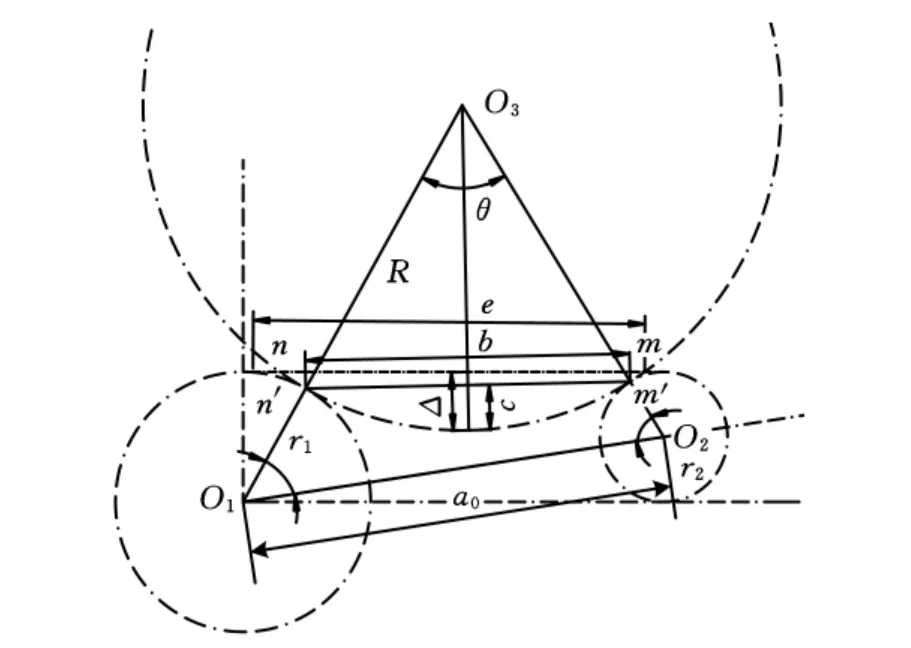
图6 简化传动几何计算分析图
(1)依据图6的几何关系可得以下方程式:
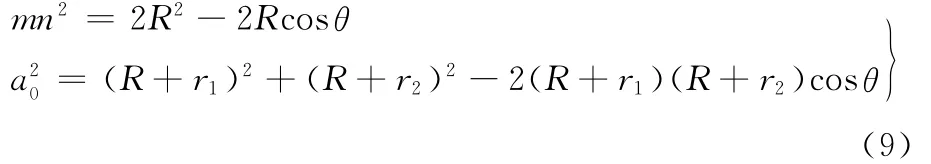
其中,R为虚拟啮合圆半径,虚拟啮合圆对应的齿数也可以是非整数值。式(9)中含有3个未知数,即解不是唯一解而是多解,故该方程是确定设计结果的条件验证式而非求解式。
(2)确定初始边界条件。初始确定链轮齿数z3时,可以参照mn直线所对应的θ角,并依此确定所对应的圆弧曲线,最终确定虚拟圆半径:
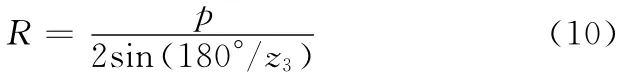
求解对应的θ角并确定mn圆弧对应的链节数,并取整数值。依据边界条件,验证是否满足约束方程:

式(11)验证最终确定的几何参数是否满足“同相位传动”的特征方程,这也是保证链传动最小不均系数Kk的条件。
2.2 阻尼器导板压入量Δ与弧度的确定
采用式(9)求解的R是多解,最终仍然要依据减振器压入量来确定其他参数。链传动松边张紧器可以根据结构的最终参数确定,但减振器压入量则根据导板表面材料的强度、耐磨特性以及加工制造等因素设计[13]。
当啮合点mn连线距离为e,压入量为Δ,改变后的啮合点m′n′连线距离为b,依据直线啮合点mn的链节数z计算分析阻尼器压入后的链节数z′。取z临近数来确定m′n′啮合点的弧长,以此弧长并参照压入量Δ求解虚拟圆弧直径R:

由于压入量在R值确定后可自行产生,故式(12)为压入量与对应的圆弧半径的初级求解方程,并以此来确定边界条件Rmin与Rmax,R值的确定还要依据中心距和发动机正时链的结构来决定。
对应张紧器圆弧半径的计算需根据直线啮合点mn的链节数t′,t′={t,t-1,t-2,…},参照图5为例,mn直线啮合点之间对应的链节数为t,取t=int(t),图6中对应角度θ的链节数为t′,代入式(9)和式(12)中求得R与c,最终设计m′n′两啮合点落于啮合圆的切点。
初始求得的R值需进行迭代以最终求得精确值,并结合实际限制确定压入量Δ和半径R。
减振导板也可以设计成“直线+圆弧+直线”、“圆弧+直线+圆弧”、“3圆弧”等多种结构形式,如图7所示。不论怎样布局最终要保证调整后的啮合点m′、n′静态位置在虚拟圆与链轮啮合点上。
设计中只分析了实际设计参数,没有考虑因为链条高速冲击磨损伸长后传递参数[14-15]的变化,在设计中可考虑以预留量来补偿磨损伸长后的影响,这个补偿量可以由阻尼器导板的压入量来调整。
3 结论
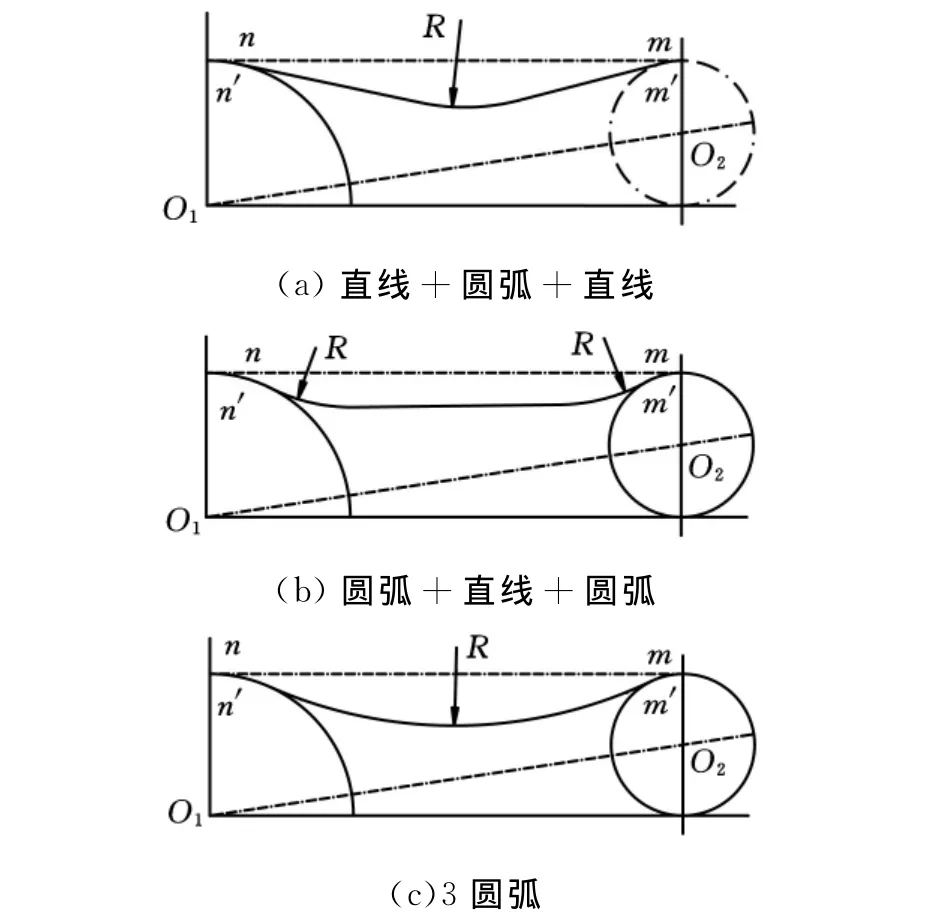
图7 阻尼器导板基本机构示意图
(1)从动轮角速度波动曲线并不是简单的正弦曲线,通过对不同链轮结构尺寸以及不同的传动初始角度变化的分析,可以看出从动轮角速度的波动曲线是变化且不规律的曲线。
(2)在高速发动机正时链设计中应尽可能地设计“同相位传动”以减小从动轮角速度ω2的波动与链传动不均系数Kk。
(3)进行高速链传动设计时,可安装阻尼器导板,并合理地选择压入量和虚拟圆半径以达到“同相位传动”效果。
[1] 郑志峰,王义行,柴帮蘅.链传动[M].北京:机械工业出版社,1984.
[2] 李长春,张景春,赵洪华.链条速度波动的影响因素[J].东南大学学报(自然科学版),2002,16(2):168-170.
[3] Conwell J C,Johnson G E.Construction and Instrumentation of a Machine to Measure Tension and Impact Force in Roller Chain Drives[J].Mechanical and Machine Theory,1996,31(4):525-531.
[4] 孟繁忠.汽车发动机链条高速性能的试验研究[J].机械工程学报,2002,38(7):62-64.
[5] Hellinger S M,Priebsch W.Prediction of Vibroacoustic Excitation Due to the Timing Chains of Reciprocating Engines[J].Proceedings of the Institution of Mechanical Engineer,Part K:Journal of Multi-body Dynamics,2003,217(3):225-240.
[6] Pedersen S L.Model of Contact between Rollers and Sprockets in Chain-drive Systems[J].Archive of Applied Mechanics,2005,74:489-508.
[7] 哈尔滨工业大学理论力学教研室.理论力学[M].北京:高等教育出版社,2002.
[8] Weber C,Herrmann W,Stadtmann J.Experimental Investigation into the Dynamic Engine Timing Chain Behaviour[J].SAE Special Publications.Engine Component Technology,1998,1317(4):137-145.
[9] Lin Yeonqchinq,Hwang Shenq-Jiaw,McDonald,et al.Dynamic Analysis of an Automotive Timing Chain System[J].American Society of Mechanical Engineers,Design Engineering Division (Publication)DE,1996,88:759-764.
[10] Wang Shukun,Meng Fanzhong.Multicycle Impact Property of Automotive Engine Timing Chain[J].Journal of Harbin Institute of Technology,2005,37(4):495-497.
[11] Conwell J C,Johnson G E.Experimental Investigation of Link Tension and Roller Sprocket Impact in Roller Chain Drives[J].Mechanical and Machine Theory,1995,31(4):533-544.
[12] 孟繁忠,李宝林,吕翔,等.汽车发动机正时链系统设计方法[J].哈尔滨工业大学学报,2009,41(5):121-124.
[13] 李宝林,孟繁忠,李延春,等.汽车发动机正时链系统失效分析[J].润滑与密封,2006,174(2):52-54.
[14] 李宝林,孟繁忠,曲少鹏,等.汽车发动机正时链试验中的纳米摩擦[J].润滑与密封,2006,181(9):90-93.
[15] 王淑坤,孟繁忠,陈亚兵,等.汽车发动机正时链的多冲特性[J].哈尔滨工业大学学报,2005,37(4):495-497.
Design of Timing Chain Parameters Based on Chain Transmission Meshing Characteristics
Li Baolin Tang Li Chu Xiaoliang Fan Shuai
China University of Mining and Technology,Xuzhou,Jiangsu,221116
The chain transmission characteristics in different initial phase angles of chain were analyzed from the perspective of geometry and the principles of virtual displacement.In addition,the effects of driven wheel angular velocity and angular inequality coefficient were analyzed with different central distances of two sprockets.The influences of initial phase angle geometry characteristic parameters of the chain transmission on driven wheel angular velocity and angular inequality coefficient degree were analyzed and the fluctuation trend of driven wheel angular velocity was found out at the same time.It is found out when the other parameters are certain,how the damper of timing chain system guides the plate pressure degree and radius curvature in order to obtain the minimum angular velocity changes and angular inequality coefficient of driven wheel.Hence the assistant formula and the validation constraint equation were provided and the ideas,as well as,the methods for the design of engine timing chain system were put forward.
chain drive characteristics;timing chain;vibration damper strip;chain drive inequality coefficient
TH11;TK4
1004—132X(2011)10—1159—06
2010—04—19
(编辑 袁兴玲)
李宝林,男,1962年生。中国矿业大学机电工程学院研究员、博士。主要研究方向为特种车辆、发动机正时系统设计及失效分析等。获发明专利3项。发表论文10余篇。唐 力,女,1962年生。中国矿业大学机电工程学院研究员。初晓亮,男,1986年生。中国矿业大学机电工程学院硕士研究生。范 帅,男,1985年生。中国矿业大学机电工程学院硕士研究生。

