直齿点线啮合齿轮传动齿间载荷分配研究
熊文恒 黄 海 周正祥
1武汉理工大学物流工程学院 武汉 430063 2江苏泰隆减速机股份有限公司 泰兴 225400
0 引言
在啮合的过程中,点线啮合齿轮传动[1]既有线接触也有点接触,具有承载能力高、传动平稳等特点,其制造简单,具有可分性、磨合性能好、磨损小的特性,齿面可制成各种硬度的齿轮[2]。但是,齿轮在啮合过程中存在单对齿和双对齿交替啮合的现象,导致齿轮齿间载荷分配大小不同且受力情况复杂,极大地影响了齿轮的传动性能和承载能力。目前国内外对渐开线齿轮齿间载荷分配的工作进行了大量研究,陆凤霞等[3]通过建立齿轮接触分析的有限元模型,利用映射法划分网格单元,结合有限元求解,得到齿轮在不同啮合位置下的载荷仿真值。包家汉等[4]以渐开线直齿圆柱齿轮为研究对象,通过建立有限元模型,分析齿轮在载荷作用下接触应力及齿间载荷分配的变化情况,认为随着齿间载荷的增大,载荷分配越平缓,啮合过程中的冲击力降低。Spitas V等[5]采用焦散的应力光学方法确定了轮齿间载荷分配率,并验证了结果的准确性。Elkholy A H、Marimuthu P等[6-8]分别以高重合度齿轮为研究对象,提出了计算齿间载荷分配率的解析模型,分析确定了轮齿间的载荷分配系数。Xie C Y等[9]以标准正齿轮为研究对象,基于最小弹性势能准则,提出了一种改进的齿间载荷分配模型,并利用有限元法研究轮毂的齿间载荷分配率,验证了模型的准确性。Marques P M T等[10]建立了正齿轮和斜齿轮的齿间载荷分配模型,精确的估算了齿轮的摩擦损失。王积森等[11]利用VB语言对Solidworks进行二次开发,得到了点线啮合齿轮的三维造型系统。杨帆等[12]通过3次样条曲线对齿轮坐标进行拟合,并利用分段法获得点线啮合齿轮的齿廓方程表达式,在Solidworks中实现了点线啮合齿轮的精确建模。
从现有的研究成果看,渐开线齿轮的齿间载荷分配研究已较全面和深入,而关于直齿点线啮合齿轮传动齿间载荷分配计算的研究尚未开展。在点线啮合齿轮传动的强度计算中,采用的仍是渐开线齿轮的齿间载荷分配系数,这对点线啮合齿轮传动的强度计算结果会有一定影响,如果全部采用仿真分析的方法效率会较低。另外,轮齿在啮合过程中各接触点所受力是轮齿啮合刚度的计算基础。因此,研究啮合过程中的点线啮合齿轮传动轮齿间载荷分配,得到相应的计算公式,能提高点线啮合齿轮传动强度计算结果的准确性和计算分析效率,也为点线啮合齿轮传动的啮合刚度研究提供了基础。
本文在总结前人研究的基础上,建立了直齿点线啮合齿轮传动的三维模型,通过分析依据渐开线齿轮齿间载荷分配计算公式的计算结果与直齿点线啮合齿轮传动有限元仿真结果,推导出直齿点线啮合齿轮传动的齿间载荷分配计算公式。
1 点线啮合齿轮的啮合特性
如图1所示,点线啮合齿轮在啮合过程中,啮合线N1N2为大小齿轮基圆的内公切线,B2点为啮合起始点即大齿轮齿顶圆与啮合线N1N2的交点。此时,小齿轮齿根的渐开线部分与大齿轮齿顶的渐开线部分接触,为凸齿廓接触;大小齿轮从B2点到节点P的啮合是凸齿廓接触;C点为双齿啮合的结束点,是单齿啮合的开始点;D点为单齿啮合的结束点,是双齿啮合的开始点。在M点啮合时,小齿轮的齿顶和大齿轮彼此完全贴合,小齿轮齿顶渐开线与大齿轮过渡曲线接触形成较大的接触面积;J点为大齿轮齿廓上渐开线与过渡曲线的分界点,当啮合位置处于J点时,小齿轮的渐开线与大齿轮齿廓过渡曲线贴合,为凹凸齿廓接触;B1点为啮合终止点即小齿轮齿顶圆与啮合线N1N2的交点。小齿轮与大齿轮在B1点脱离啮合时,小齿轮齿廓对应的渐开线与大齿轮的过渡曲线接触,接触点很接近大齿轮的J点,但会在J点以下。在啮合传动的过程中,由B2点到M点的啮合为凸齿廓接触,M点到B1点的啮合为凹凸齿廓接触。

图1 齿轮啮合点位置图
2 点线啮合齿轮齿廓曲线方程
本文研究中所采用的点线啮合齿轮齿廓曲线方程参考文献[1]中关于点线啮合齿轮齿廓曲线方程的理论研究部分。
2.1 齿条型刀具加工时被切齿轮的普遍方程式
如图2所示,假设静坐标系XOY固定在轮齿坯上,坐标系原点O则是轮齿坯的中心。在已知轮齿齿条齿廓上的所有点在动坐标系X1PY1中坐标的前提下,可以得到被加工齿轮的齿廓上所有静坐标系XOY上的点坐标,从而得到点线啮合齿轮的齿廓方程式。

图2 齿轮坯上的静坐标系
被加工齿轮齿廓的方程式为

式中:r为分度圆半径,x1、y1为齿廓上的点坐标,φ为齿条刀具的滚动角。
2.2 点线啮合齿轮上的过渡曲线方程式
如图3所示,曲线bJc为点线啮合齿轮的齿廓曲线,其中曲线bJ为过渡曲线,曲线Jc为渐开线,ra为齿顶圆半径,rf为齿根圆半径,r为分度圆半径,rJ为J点半径。
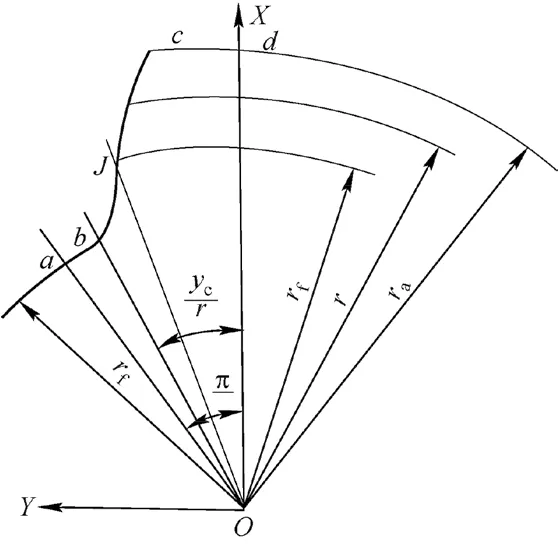
图3 点线啮合齿轮大齿轮齿廓
点线啮合齿轮齿廓过渡曲线bJ段的方程式为
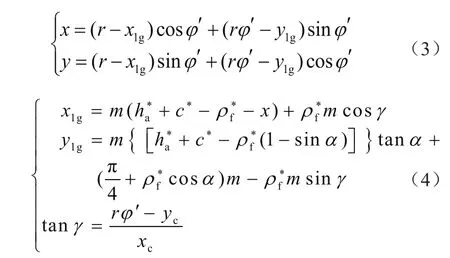
式中:ρ*f为圆角半径系数,h*a为齿顶高系数,α为压力角。
2.3 点线啮合齿轮上J点的方程
J点的齿廓方程式为
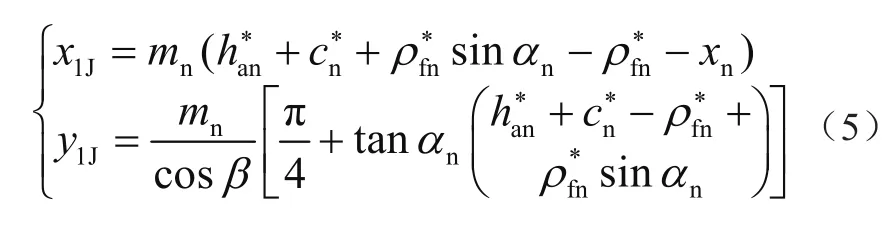
式中:c*n为法向顶隙系数;h*an为法面齿顶高系数。
3 渐开线齿轮齿间载荷分配计算公式
啮合齿轮齿间载荷分配系数LSF(Load-sharing factor)是指在一个啮合周期内,每一个啮合齿轮所承担整个传动载荷的比率。其表达公式为

式中:LSF为啮合齿轮齿间载荷分配系数,Pi为单对齿承受的载荷值,P为齿轮副中的一个齿轮沿接触路径所承受的总载荷。
3.1 AGMA标准渐开线齿轮齿间载荷分配计算公式
图4为啮合齿轮的主动轮在转角分别为ω=0°、ω=θLPSTC、ω=θHPSTC和ω=θ时的啮合位置图。
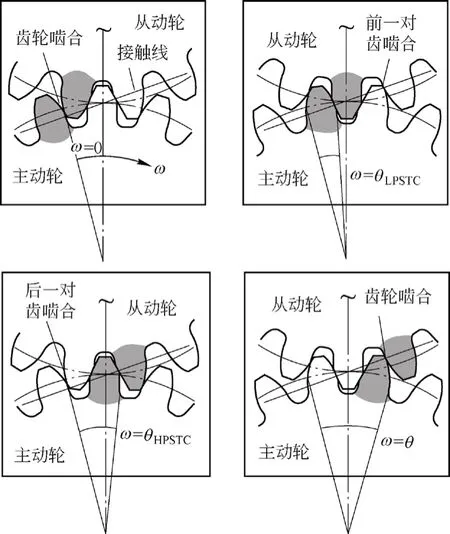
图4 齿轮传动啮合位置图
在AGMA B88(American Gear Manufactur-ers Association)标准[5]中,啮合齿轮的载荷分配系数公式为
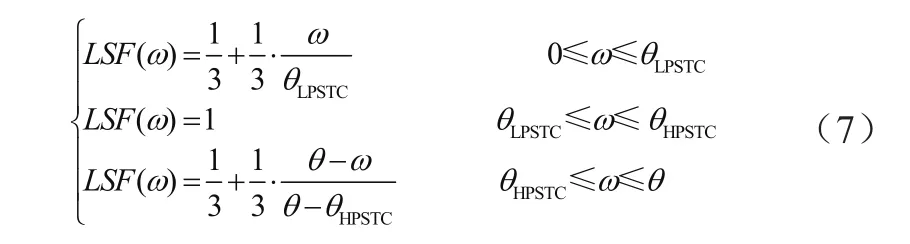
式中:ω为主动轮啮合所在位置的转角,θLPSTC为齿轮进入到单齿啮合时主动轮的转角,θHPSTC为齿轮进入到双齿啮合时主动轮的转角,θ为齿轮脱离啮合时主动轮的转角。
3.2 ISO国际标准渐开线齿轮齿间载荷分配计算公式
在ISO 6336国际标准[5]中,啮合齿轮的载荷分配系数公式为
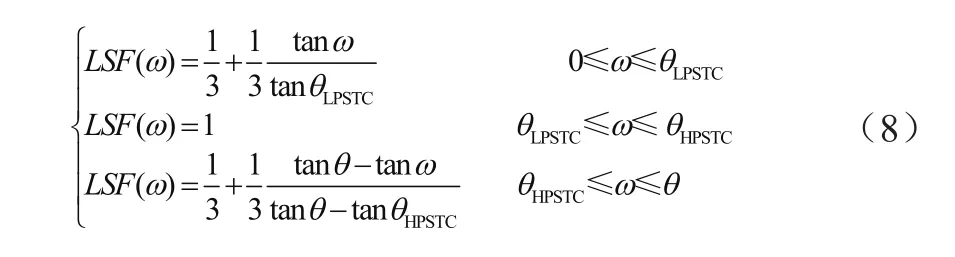
3.3 渐开线齿轮齿廓参数公式
由于齿轮在啮合过程中,2齿的曲率半径之和是恒定的,所以为了更好地描述接触点,José I. Pedrero等[13,14]在考虑轮齿啮合过程中的弯曲、剪切变形和压缩变形时,利用最小弹性势能准则(MEPE),建立了标准正齿轮和斜齿轮沿接触线的负载分配模型,同时推导了渐开线齿轮齿廓参数公式,具体公式为
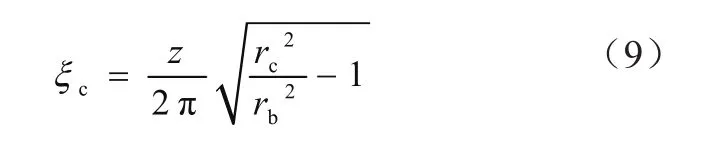
式中:ξc为主动轮所在啮合位置下的齿廓参数,z为主动轮的齿数,rb为基圆半径,rc为接触点半径。
图5为渐开线齿轮的几何形状图。
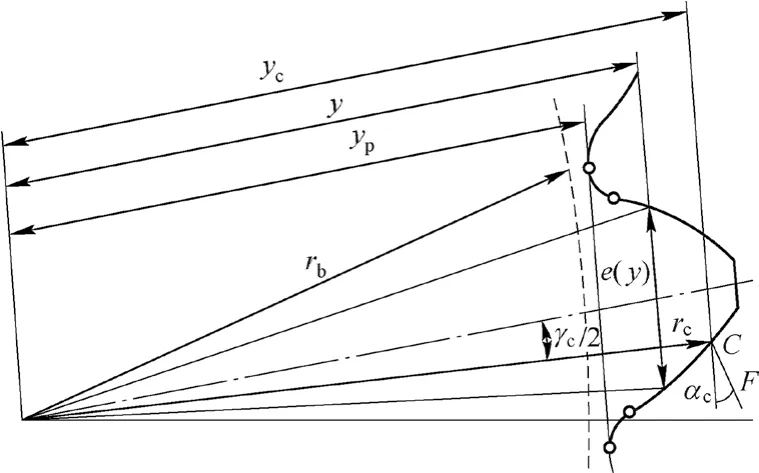
图5 渐开线齿轮的几何形状图
由于啮合齿轮在不同啮合位置下的接触半径不同,所承受的载荷也有所变化,在充分考虑这些因素后,利用啮合齿轮在相应的接触路径及不同啮合位置下的接触比得到了啮合齿轮齿间载荷分配系数。具体公式为
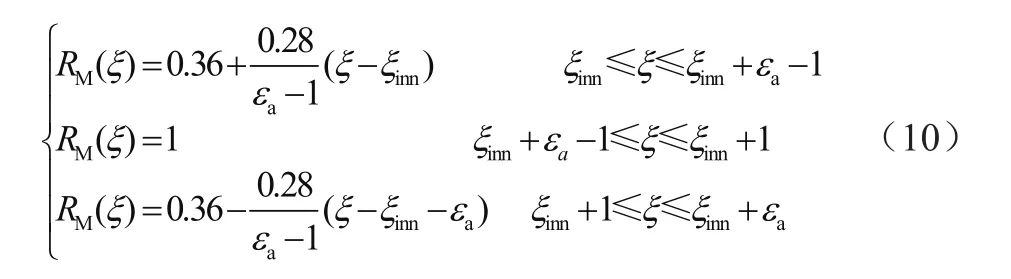
式中:ξ为主动轮的渐开线齿轮齿廓参数,ξinn为啮合齿轮刚开始啮合时主动轮的齿廓参数,εα为啮合齿轮的重合度值。
4 点线啮合齿轮传动的三维建模
本文所研究的直齿点线啮合齿轮主要参数的选择如表1所示,其中主动轮为小齿轮,从动轮为大齿轮。
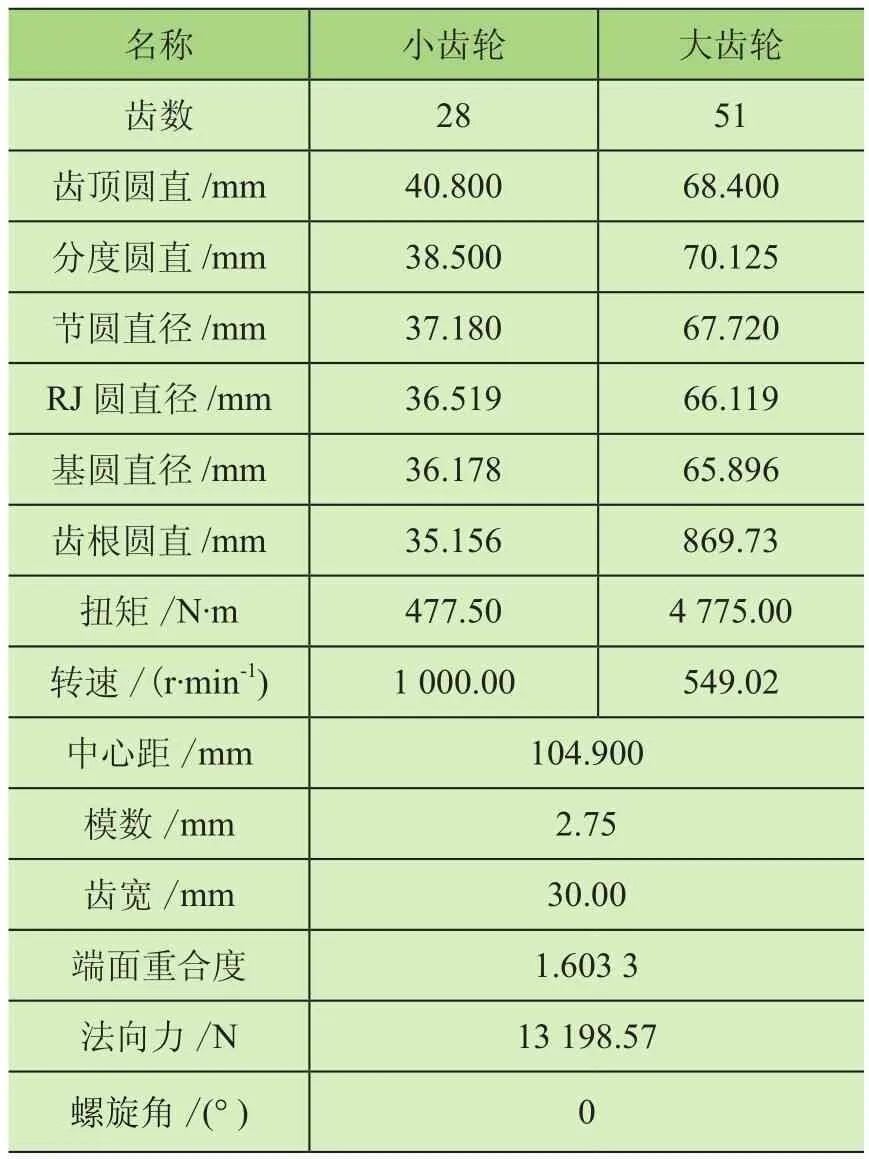
表1 一对点线啮合齿轮的基本参数
根据表1中的齿轮参数,在Solidworks软件中对点线啮合齿轮传动大、小齿轮进行三维建模,并完成齿轮的啮合装配。图6、图7所示分别为点线啮合齿轮传动大、小齿轮的齿廓曲线图。

图6 大齿轮齿廓曲线图

图7 小齿轮齿廓曲线图
本文主要研究点线啮合齿轮在1个啮合周期内的齿间载荷的分配情况,为了提高计算效率,采用了齿轮的5对齿进行装配仿真分析。图8为点线啮合齿轮传动大小齿轮的装配体图。
图8 点线啮合齿轮传动装配体图
5 有限元仿真分析
为更好地对点线啮合齿轮传动的齿间载荷分配进行研究分析,假设点线啮合齿轮的轮体为刚性体,即在有限元分析前将轮齿的弹性模量在原来的基础上扩大一万倍[15],弹性模量E=2×109MPa。
5.1 点线啮合齿轮传动的有限元分析前处理
在Ansys Workbench静力学分析模块中,将点线啮合齿轮的材料设置为合金钢,即20CrMnMo,材料弹性模量E=2×109MPa,泊松比为0.3。
本文采用面-面接触的方式,选择小齿轮啮合面为接触面,大齿轮啮合面为目标面,接触类型为有摩擦接触(Frictional),设置摩擦系数为0.1,网格采用六面体主导的划分方法。图9为点线啮合齿轮网格划分图。

图9 点线啮合齿轮网格划分图
对从动轮施加固定约束(Fixed Support),主动轮施加圆柱面约束(Cylindrical Support),限制主动轮的径向旋转自由度(Radial)和轴向旋转自由度(Axial),释放其切向旋转自由度(Tangential),同时对主动轮施加477.5N·m的扭矩,使得主动轮绕轴线顺时针旋转。图10为点线啮合齿轮约束设置图。
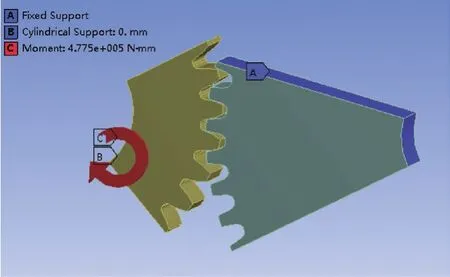
图10 点线啮合齿轮约束设置图
5.2 有限元仿真结果
利用有限元仿真得到点线啮合齿轮传动在不同啮合位置下的齿间载荷仿真值。表2为在刚性体条件下,点线啮合齿轮传动在B2点 (ω=0°)、C点 (ω=7.88°)、D点(ω=12.85°)和B1点 (ω=20.74°)的齿间载荷仿真值和载荷分配率。
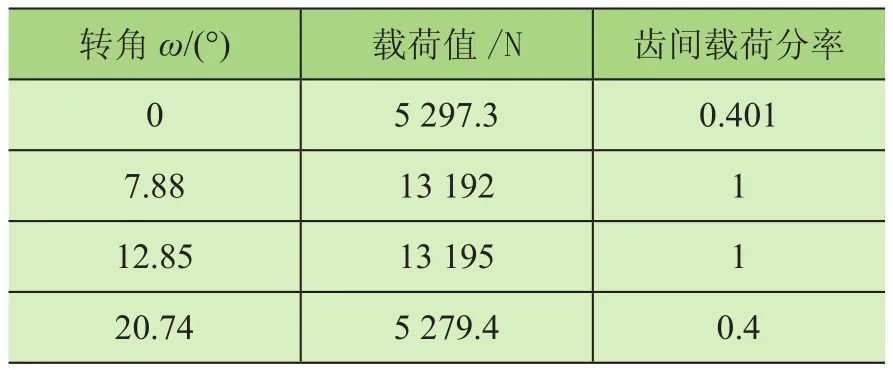
表2 刚性体条件下齿轮齿间载荷仿真值和分配率
图11为基于有限元仿真齿间载荷分配率,结合表2可知,点线啮合齿轮传动在刚开始进入啮合时,齿轮承受载荷突变为5 297.3 N,此时齿轮齿间载荷分配率为0.401;当主动轮转角增加到7.88°时,齿轮承受载荷达到最大值为13 192 N;此后,主动轮转角在7.88°~12.85°时,齿轮承受的载荷最大且基本保持不变;当主动轮转角大于12.85°时,齿轮受载荷值开始逐渐下降,并在20.74°即齿轮开始脱离啮合时,达到最小值为5 279.4 N,此时齿轮齿间载荷分配率为0.4。

图11 基于有限元仿真齿间载荷分配率
将图11拟合成直线,从而得到图12所示点线啮合齿轮传动的齿间载荷分配率图。
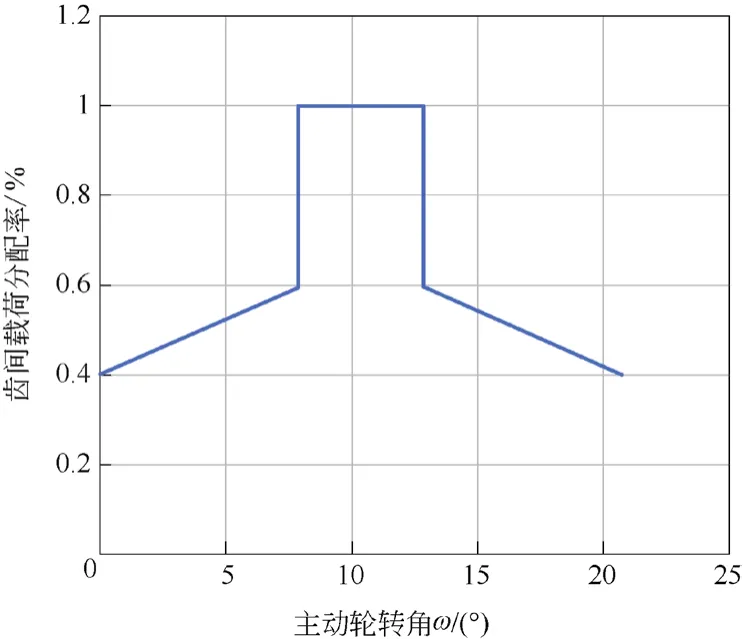
图12 点线啮合齿轮传动齿间载荷分配率
6 结果分析
按式(7)、式(8)和式(10)分别得到理论计算的点线啮合齿轮传动齿间载荷分配率,并将结果与有限元仿真得到的点线啮合齿轮传动的齿间载荷分配率进行对比分析。
图13为基于AGMA B88标准计算得到的点线啮合齿轮传动齿间载荷分配率,齿轮在刚进入啮合时,齿轮齿间载荷值占总载荷的33.3%。当主动轮转角为7.88°时,载荷值突然增大,齿轮齿间载荷值占总载荷的66.7%。当主动轮转角在7.88°~12.85°时,齿轮承受载荷最大且基本保持不变。当主动轮转角大于12.85°时,齿轮齿间载荷值开始突然下降,载荷分配率由100%下降到66.7%。在主动轮转角为20.74°时,齿轮齿间载荷值下降到最小且占总载荷的33.3%,齿轮脱离啮合,啮合周期结束。

图13 基于AGMA B88标准齿轮齿间载荷分配率
图14为基于ISO 6336国际标准计算得到的点线啮合齿轮传动齿间载荷分配率,可以看出ISO 6336国际标准公式与AGMA B88标准公式计算得到的齿轮齿间载荷分配率相近。齿轮在刚进入啮合时,齿轮齿间载荷值占总载荷的33.3%。当主动轮转角为7.88°时,载荷值突然增大,此时齿轮齿间载荷值占总载荷的66.7%。当主动轮转角在7.88°~12.85°时,齿轮承受载荷最大且基本保持不变。当主动轮转角大于12.85°时,齿轮齿间载荷值开始突然下降,载荷分配率由100%下降到66.7%。在主动轮转角为20.74°时,齿轮齿间载荷值下降到最小且占总载荷的33.3%,齿轮脱离啮合,啮合周期结束。
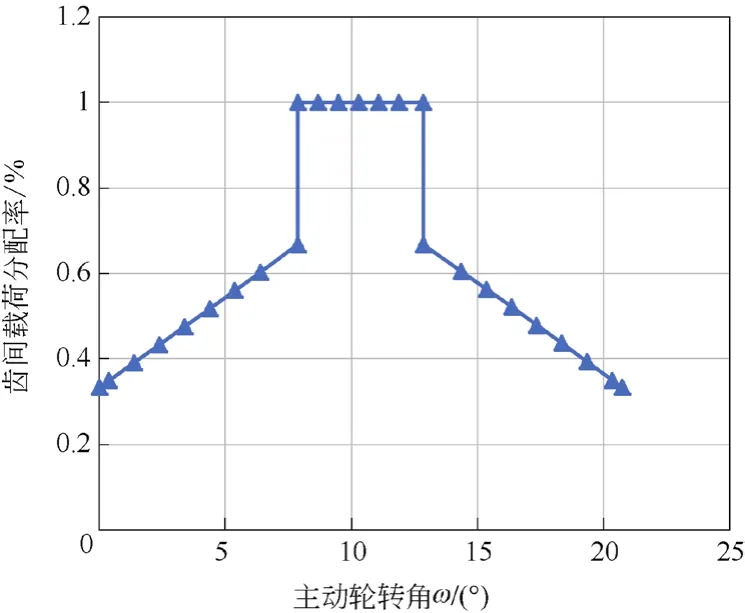
图14 基于ISO 6336标准齿轮齿间载荷分配率
图15为基于渐开线齿轮齿廓参数公式计算得到的点线啮合齿轮传动齿间载荷分配率,此公式与前2个公式计算得到的载荷分配率有所不同。齿轮在刚进入啮合时,齿轮齿间载荷值占总载荷的36%。当主动轮转角为7.88°时,载荷值开始突然增大,此时齿轮齿间载荷值占总载荷的64%。当主动轮转角在7.88°~12.85°时,齿轮承受载荷最大且基本保持不变。当主动轮转角大于12.85°时,齿轮齿间载荷值突然下降为总载荷的64%。在主动轮转角为20.74°时,齿轮齿间载荷值下降到最小且占总载荷的36%,齿轮脱离啮合,啮合周期结束。

图15 基于渐开线齿轮齿廓参数公式齿间载荷分配率
图16为点线啮合齿轮传动齿间载荷分配率的有限元仿真分析结果。由式(7)、式(8)、式(10)理论计算结果的对比图可以看出,点线啮合齿轮传动齿间载荷分配率的有限元仿真结果与理论计算结果有所不同。点线啮合齿轮传动在B2点(ω=0°)即刚开始进入啮合时,齿轮齿间载荷分配率为0.401,大于理论计算的齿间载荷分配率。在B1点(ω=20.74°)即脱离啮合时,齿轮齿间载荷分配率为0.4,也大于理论计算的齿间载荷分配率。
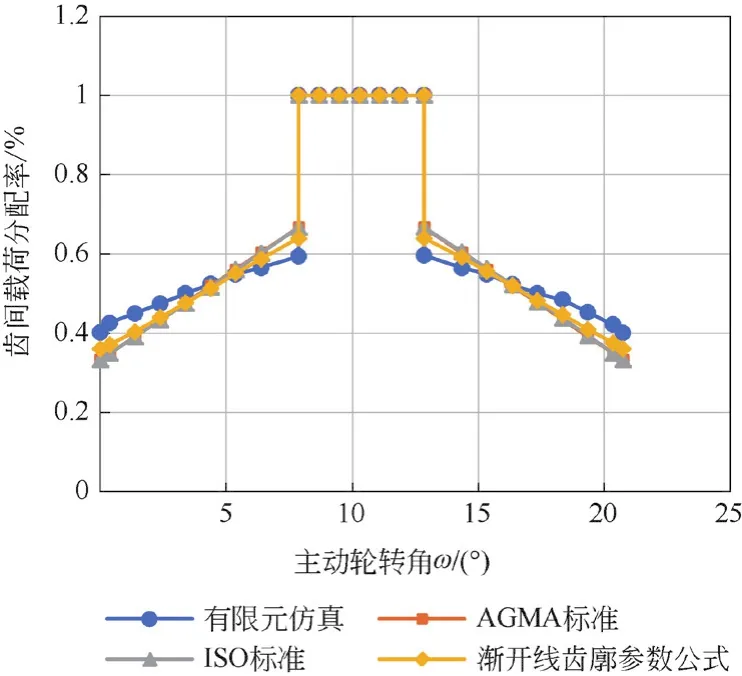
图16 齿间载荷分配率有限元仿真与理论计算对比图
由于点线啮合齿轮传动在刚进入啮合即B2点(ω=0°)时的齿间载荷分配率为0.401,随着主动轮转角的增大,点线啮合齿轮传动的齿间载荷分配率呈线性增长,增长斜率为1/5。随着主动轮继续转动,在脱离双齿啮合开始进入单齿啮合即C点(ω=7.88°)时,点线啮合齿轮传动的齿间载荷分配率为1。在θLPSTC≤ω≤θHPSTC时,齿间载荷分配率保持不变。随着主动轮转角的继续增大,在脱离单齿啮合开始进入双齿啮合即D点(ω=12.85°)时,点线啮合齿轮传动的齿间载荷分配率开始呈线性下降趋势,斜率为1/5。B1点(ω=20.74°)即齿轮脱离啮合时,齿间载荷分配率下降到最小值为0.4。结合AGMA B88标准和ISO 6336国际标准以及图12得到点线啮合齿轮传动的齿间载荷分配计算公式为

式(11)、式(12)主要适用于在刚性体条件下,对点线啮合齿轮传动的齿间载荷分配率进行高效快捷的计算,为以后研究点线啮合齿轮传动的啮合刚度的问题提供理论依据。
7 结论
1)渐开线齿轮齿间载荷分配计算公式不适用于点线啮合齿轮传动。
2)仿真结果表明,点线啮合齿轮传动在啮合过程中,轮齿所受力的变化仍然接近于线性变化。
3)点线啮合齿轮传动在刚进入啮合即B2点时齿轮齿间载荷由零突然增大到总载荷的2/5,故需考虑齿轮在刚开始啮合时所受载荷冲击对轮齿的破坏。
4)点线啮合齿轮传动在双齿啮合开始时的B2点和双齿啮合结束时的B1点的载荷占总载荷的2/5,而在双齿啮合结束时的C点和双齿啮合开始时的D点的载荷占总载荷的3/5。

