有限域上的方程与不可约多项式

田 力，孙宗明

(泰山学院数学与系统科学学院，山东泰安 271021)

本文研究有限域上的若干方程与若干不可约多项式，根据具体情况，将用不同的记号表示有限域.本文中，0表示域的零元，e表示域的单位元.本文所使用的符号是标准的，有限域和有限群的基本知识被认为是熟知的，见文献［1－2］.

1 若干方程

本款讨论有限域上的若干方程以及相关的若干问题.

1.1 方程xq+1=λ与xq+x=μ

本段在p2k元域上研究问题，记q=pk，则p2k=q2，并且，把p2k元域记为Fq2，把pk元域记为Fq，本段参见文献［3－4］.

先研究Fq2的一个自同构，它扮演着重要的角色.设

则σ是Fq2的自同构，并且，σ的阶为2，事实上，首先，σ不是恒等映射，因为，若记Fq2的非零元素乘群为F*q2=〈c〉，则有σ(c)≠c;其次，σ2必为恒等映射，因为，对于任意的a∈Fq2，均有

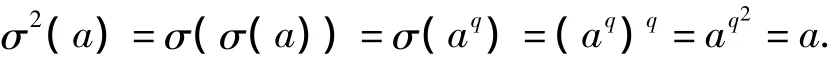
另外，对于a∈Fq2，有

因此，Fq2的自同构σ的固定子域是Fq.

现在研究Fq2上的方程xq+1=λ，而λ≠0，此时，可以在群F*q2中考虑.设

则τ是F*q的同态映射.记π的象为G，核为N.由群同态基本定理得F*q2/N与G同构，且o(F*q2)= o(N)o(G).显然，N是方程xq+1=e所有解的集合，所以，o(N)≤q+1.因为，

所以，o(G)≥q－1.但是，G是F*q的子群，从而，o(G)=q－1，τ是满射.因此，对于λ∈F*q2，一定有y0∈，使得τ(y0)=λ，即y0q+1=λ，方程xq+1=λ有解x=y0.由o()=q－1得o(N)=q+1，从而，方程xq+1=e恰有q+1个解.因为方程xq+1=λ的解y0乘以方程xq+1=e的任一个解均得到方程xq+1=λ的解.群中一方程的解就是域中该方程的根，这样，就有下面的

定理1.1.1 有限域Fq2上的方程xq+1=λ(λ≠0)在Fq2中恰有q+1个根.

现在研究Fq2上的方程xq+x=μ.设

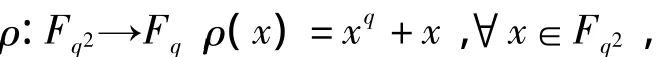
则ρ是加群Fq2到加群Fq的同态映射.类似于上面的讨论可得，ρ是满射.同样类似于上面的讨论可得，方程xq+x=0起着与方程xq+1=e一样的作用，此处详细的推导从略.这样，就有下面的

定理1.1.2 有限域Fq2上的方程xq+x=μ在Fq2中恰有q个根.

1.2 方程xps－x－c=0

本段在pk元域上研究问题，将pk元域记为F.

视F为加群，当s=1时，作

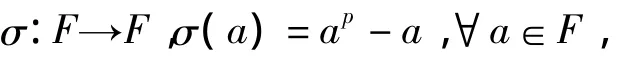
则σ是加群F到F的同态映射.σ的同态核是Fp，而Fp是F的p元子域.有下面的

定理1.2.1 设xp－x－c=0(c∈F)是F上的方程，则

1)xp－x－c=0(c∈F)在F中有根当且仅当有a∈F使c=ap－a;

2)F中恰有pk－1个c，使xp－x－c=0(c∈F)在F中有根;

3)若xp－x－c=0(c∈F)在F中有根，则其在F中恰有p个根;

当s＞1且s|k时，pk元域F有ps元子域Fps.上面的σ变为

σ是加群F到F的同态映射，σ的同态核是Fps.可以得到下面的

定理1.2.2 设xps－x－c=0(c∈F)是F上的方程，s＞1且s|k，则

1)xps－x－c=0(c∈F)在F中有根当且仅当有a∈F使c=aps－a;

2)F中恰有pk－s个c，使xps－x－c=0(c∈F)在F中有根;

3)若xps－x－c=0(c∈F)在F中有根，则其在F中恰有ps个根.

当s＞1但s不整除k时，记w=(s，k)，s=μw，此时，研究F的子域Fpw，有结论:对于∀a∈Fpw，成立aps=apw.

仍然研究

σ是加群F到F的同态映射，σ的同态核包含Fpw，从而就得到下面的

定理1.2.3 设xps－x－c=0(c∈F)是F上的方程，s＞1但s不整除k，记w=(s，k)，则

1)xps－x－c=0(c∈F)在F中有根当且仅当有a∈F使c=aps－a;

2)F中至多有pk－w个c，使xps－x－c=0(c∈F)在F中有根;

3)若xps－x－c=0(c∈F)在F中有根，则该方程在F中至少有pw个根.本段中定理的详细证明参见［5］，此处从略.

1.3 降次定理

一般而言，方程的次数越低，讨论问题越相对容易.本段从这一角度研究有限域上的方程，本段参见［6］.

本段在pk元域上研究问题，将pk元域记为F.因为，Fpl=F(l为正整数)，所以，得到下面的

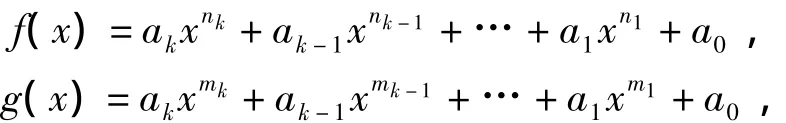
定理1.3.1 设是F［x］中的多项式，ni，mi，ni=plmi(i=0，1，…，k－1，k)均为正整数，则

1)若α∈F是方程f(x)=0的一个根，则αpl是方程g(x)=0的一个根;

2)若β∈F是方程g(x)=0的一个根，则有γ∈F是方程f(x)=0的一个根.

求F上的方程的根，可以转化为求F上的次数＜pk的某一方程的根，即有下面的

定理1.3.2 设

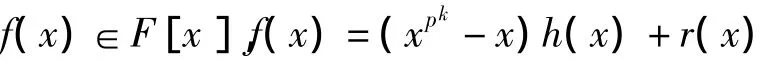
h(x)，r(x)∈F［x］，并且r(x)=0或deg(r(x))＜pk，则

1)当r(x)=0时，F的元素均为方程f(x)=0的根;

2)当r(x)≠0时，方程f(x)=0与r(x)=0在F中的根的集合相同.在上面定理的1)中，方程f(x)=0在F必有重根，于是，就有下面的问题1.3.3 在定理1.3.2的1)的情况下，方程f(x)=0在F中重根的状况.

1.4 二项方程的降次与求根

本段在pk元域上研究问题，将pk元域记为F，本段参见文献［7－8］.研究二项方程的降次，有下面的

定理1.4.1 设

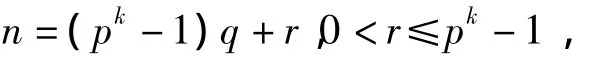
其中q，r是整数，则方程xn=b与xr=b在F中有相同的根的集合.

实际上，方程的次数可以进一步降低，即有下面的

定理1.4.2 设

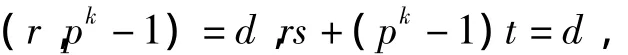
其中r，d均为正整数，s是整数，则xr=b在F中的根是xd=bs的根.

定理1.4.3 设d|(pk－1)，m是c在F的非零元素乘群F*中的阶，则xd=c在F中的根是xdm=e的根.

定理1.4.4 设

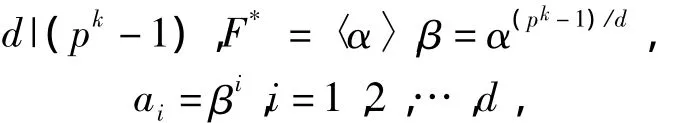
则a1，a2，…，ad是xd=e在F中的不同的根.

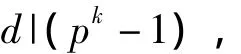
定理1.4.5 设a0是xd=c在F中的一个根，

a1，a2，…，ad

是xd=e在F中的不同的根，则

是xd=c在F中的不同的根.

上述的五个定理容易证明，此处从略.根据这五个定理，设计出求根的具体方法，有下面的

方法1.4.6 求二项方程的根的方法如下:

第一步，由定理1.4.1与1.4.2，将xn=b的次数降低，化为xd=bs=c，并且，d|(pk－1);

第二步，记定理1.4.3中的dm=w，解决xw=e，由定理1.4.1与1.4.2，将xw=e转化为xd1=e，并且，d1|(pk－1)，再由定理1.4.4，求出xd1=e的d1个根;

第三步，由定理1.4.3，xd=c是xw=e的根，求得xw=e的一切根后，代入验证，得到xd=c的一个根a0;

第四步，由定理1.4.4，得到xd=e的d个根a1，a2，…，ad，从而，由定理1.4.5得到xd=c的d个根a0a1，a0a2，…，a0ad;

第五步，由定理1.4.2，将xd=c的根代入xn=b，进行验证，以得到xn=b的根.

2 不可约多项式

本款中，将pk元域记为F.

2.1 筛法

本段给出确定F上的不可约多项式的方法.

F上的次数≥1而≤n的多项式有有限个.一般地，F上的s次多项式有(q－1)qs个，其中，q=pk，并且，可以按一定程序将它们排列出来.于是，就可以将F上的次数≥1而≤n的多项式按一定程序全部排列出来，且次数小的在前，次数大的在后.

这样排好之后，就可以仿照求素数的筛法进行.做法是:将排在最前面的多项式圈起来，而后划去它的一切倍式，剩下的没有圈且没有划去的多项式中，排在最前面的是不可约多项式，将它圈起来，再划去它的一切倍式，如此下去，直至最后一个被圈的多项式为止.所有被圈起来的多项式都是F上的不可约多项式，且是次数≥1而≤n的全部不可多项式.

所给出的方法称为确定F上的不可约多式的筛法.

2.2 Berlekamp法

熟知，在有理数域上，有下面的

克朗奈格定理.设f(x)是n(n＞0)有理系数多项式，则f(x)可以经有限次有理运算在有理数域上分解为不可约多项式的乘积.

克朗奈格定理的证明同时给出了具体做法，但是太麻烦了，麻烦到简直无法实施的地步.

有Berlekampd的一个方法，利用该方法，总是可以将F上的任一个多项式f(x)分解为F上的两两两不同的不可约多项式的幂的乘积，从而也就判定了f(x)是否为不可约多项式，进一步，可以求出F上的次数≥1而≤n的全部的不可约多项式.

Berlekampd的这个方法，此处从略，参见［9］.将Berlekampd的这个方法称为Berlekampd法.

2.3 多项式的可约性

为了确定有限域上的不可约多项式，了解并掌握一些多项式的可约性当然是有益的和必要的.本段中为了方便而将域的单位元记为1，本段参见［10］.对于任意的域，成立下面的

定理2.3.1

1)若域F上的多项式f(x)的零次项为零，则f(x)在F上可约⇔f(x)的次数＞1;

2)域F上的二次多项式f(x)在F上的可约⇔存在α∈F，使得f(α)=0;

3)域F上的三次多项式f(x)在F上的可约⇔存在α∈F，使得f(α)=0;

4)若f(x)是域F上的多项式，a，b∈F，a≠0，则f(x)在F上可约⇔f(ax+b)在F上可约;

5)若域F上的多项式f(x)满足条件(f(x)，f'(x))≠1，则f(x)在F上可约.

上面的定理中的4)是多项式的未定元的替换问题，参见［11］，此处从略.而其他的均容易得出.

定理2.3.2 设f(x)是pk元域F上的多项式.若f(x)的每一项的次数均为p的方幂，则f(x)在F上可约.

定理2.3.3 设f(x)是2k元域F上的多项式.若f(x)的项的系数均为1，并且有偶数个项，则f(x)在F上可约.

作为定理的应用，有下面的

例2.3.4 二元域F上的三次不可约多项式.记F={0，1}，F［x］中有8个三次多项式:x3+x2+x +1，x3+x2+x，x3+x2+1，x3+x2，x3+x+1，x3+x，x3+1，x3.根据定理2.3.1的1)，x3+x2+x，x3+x2，x3+x，x3均可约;因为1是x3+x2+x+1，x3+1的根，所以，根据定理2.3.1的3)，它们均不可约;因为0，1均不是x3+x2+1，x3+x+1的根，所以，根据定理2.3.1的3)，它们均不可约.因此，F［x］中的三次不可约多项式是:x3+x2+1，x3+x+1.

2.4 任意高次的不可约多项式

熟知，有理数域上存在任意高次的不可约多项式，有限域也是如此，本段参见文献［12－14］.设F是pk元域，作F［x］中的多项式xpkm－x在F上的分裂域

E=F(α1，α2，…，αpkm)，其中α1，α2，…，αpkm是xpkm－x的全部根，则E恰由xpkm－x的两两互异的pkm个根组成，E是pkm元域.E是F的m次扩域，又E是F的单扩域，E=F(α)，α在F上的极小多项式f(x)是F上的m次不可约多项.这样，就得到下面的

定理2.4.1 设F是pk元域，m是任意正整数，则F上存在m次不可约多项式.

实际上，该定理前面的叙述，已经给出了该定理的一个证明.为了给出该定理的另一个证明，要用到下面的引理，证明从略.为方便，记pk=q.

引理2.4.2

1)qn－1|qm－1⇔n|m;

2)xqn－1－1|xqm－1－1⇔n|m;

3)设p(x)是F中的n次不可约多项式且p(0)≠0，则p(x)|xqm－1－1⇔n|m.

定理2.4.1的证明:当m=1时，x就是F上的m次不可约多项式.

当m＞1时，研究F上的多项式

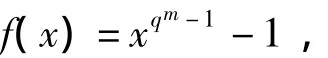
它分解为F［x］中的不可约多项式的乘积，而由引理知，f(x)的不可约因式的次数必整除m，从而其次数≤m.现在计算f(x)的次数＜m的一切不可约因式的次数之和M.

因为，xqs－1－1与其导数

互素，所以，xqs－1无重因式.当s＜m时，由引理知，f(x)的一切s次不可约因式均为xqs－1的因式，它们两两互素，从而它们的乘积也为xqs－1－1的因式，所以，它们的次数之和≤qs－1.于是，让s=1，2，…，m－1，就得到

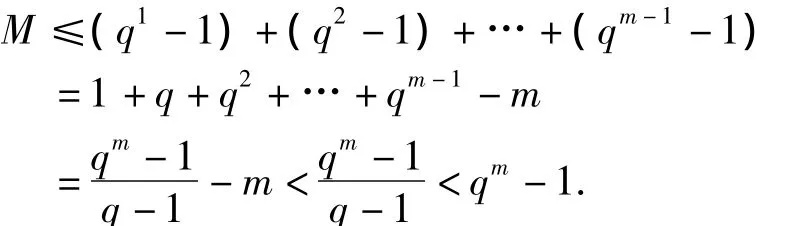
因此，f(x)必有m次不可约因式g(x)，即F［x］中有m次不可约多项式g(x).

定理2.4.3 设pd(x)是F［x］中所有首项系数为1的d次不可约多项式的乘积，当d=1时x除外，则

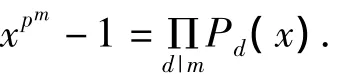
证明 F［x］中首项系数为1的任一个d次不可约多项式都是pd(x)的因式，而pd(x)的任意两个首项系数为1的d次不可约因式都彼此互素，所以，由引理2.4.2，当d|m时

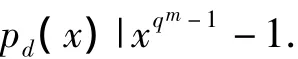
另一方面，由引理2.4.2，xqm－1－1的每一个d次不可约因式都是dΠ|mPd(x)的因式，而xqm－1－1没有重因式，所以

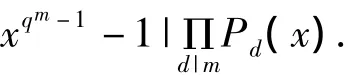
因此，根据dΠ|mPd(x)的首项系数为1，就得到

2.5 多项式的根与不可约性

本段中，就一类多项式研究其有根与不可约性的关系.所研究的域F仍然是pk元域，1表示域的单位元.

定理2.5.1 若xp－x－c=0(c∈F)在域F中没有根，则多项式xp－x－c(c∈F)在F［x］中不可约.

证明 用反证法.设f(x)=xp－x－c在F［x］可约，则可取f(x)的m(0＜m＜p)次首项系数为1的因式g(x)∈F［x］.在f(x)的分裂域E中，g(x)有根r，从而，有Fp的m个元素f1，f2，…，fm，使r+f1，r+ f2，…，r+fm为g(x)在E中的m个互异的根.于是，在E［x］中，就有

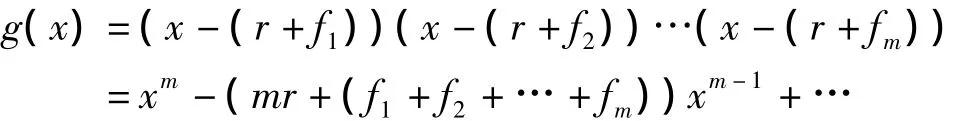
从而

又

12m，

所以，mr∈F.再由于mr=(me)r，me∈F，me≠0，所以r∈F，引出矛盾.

容易证明，xp－x－c=0(c∈F)在F中或者有p个根，或者没有根.于是，就有下面的

定理2.5.2 F上的多项式xp－x－c(c∈F)在F［x］或者不可约，或者完全分裂.

在下面的情况下，仅成立

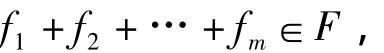
定理2.5.3 设s是正整数且s|k，xps－x－c=0(c∈F)在F中没有根，则多项式xps－x－c(c∈F)在F［x］中没有m次真因式，其中p不整除m.

证明 反证法.设f(x)=xps－x－c在F［x］中有m次首项系数为1的真因式g(x).在f(x)的分裂域E中，g(x)有根r，从而，有Fps的m个元素f1，f2，…，fm，使r+f1，r+f2，…，r+fm为g(x)在E中的m个互异的根.于是，在E［x］中，就有

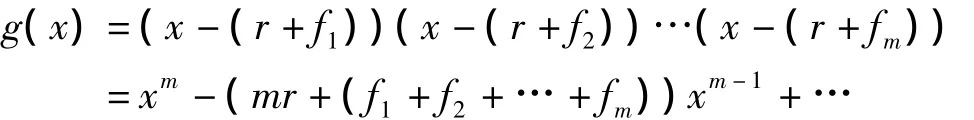
由于g(x)∈F［x］，所以

又

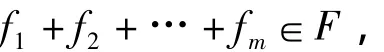
所以，mr∈F.再由于mr=(me)r，me∈F，并且，p不整除m，所以me≠0，因此，r∈F，引出矛盾.

对于一般的情况，类似的结论如何，作为遗留问题，需要作进一步的研究，参见［5］.

3 不可约多项式的根号解

本款中，就不可约多项式的根，进一步作一些探讨.为方便，记pk=q，记pk元域为Fq.

先研究Fq［x］中不可约多项式的根的一些性质，证明见［15－16］.

定理3.1 Fq［x］中的不可约多项式没有重根.

定理3.2 设f(x)∈Fq［x］是Fq上的m次不可约多项式，α是f(x)的一个根，则

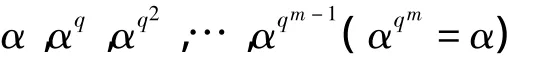
恰为f(x)的m个互不相同的根，α在Fq的扩域Fqm中且Fqm=Fq(α)就是f(x)在Fq上的分裂域.

多项式的根号解曾经是16至18世纪的250余年期间的热门问题，吸引并困惑了诸如拉格朗日这样的大数学家，19世纪20至30年代，相继被挪威年轻(只活了27岁)数学家阿贝尔和法国更年轻的(只活了20岁)数学家伽罗瓦所解决，并开启了抽象代数学的新纪元.

对于有限域而言，不可约多项式的根号解问题却较为简单，［17］讨论了这一问题，将主要结果列出

如下，证明从略.

引理3.3

1)Fq恰由Fq［x］中的约多项式xpk－x的所有的根组成.

2)设f(x)∈Fq［x］是Fq上的m次不可约多项式，则f(x)|xqn－x⇔m|n.3)设Fqm是Fq的m次扩域，则Fqm的保持Fq的元素不变的所有自同构组成的群G是m阶循环群.引理中的群G称为Fqm对于Fq的伽罗瓦群，并且，有Fq［x］中的m次多项式f(x)，使得Fqm= Fq(α)，而α是f(x)的一个根，就将G称为f(x)的伽罗瓦群.

定理3.4 设f(x)∈Fq［x］是Fq上的m次不可约多项式，则f(x)的伽罗瓦群G同构于某个置换群〈(12…m)〉.

定理3.5 设f(x)∈Fq［x］是Fq上的m次不可约多项式，Fq的特征p不整除m，则f(x)可以根号解.

在讨论根号解时，要用到单位根和本原单位根的结论，［18］和［19］较多地进行了研究，所得的结果是重要的，不少情况下都要用到，此处均从略.

4 其他相关问题

4.1 线性矩阵方程组

［20］类似于［21］建立了pk元域F上的线性矩阵方程组的理论，给出了下面的结果，证明从略.

定理4.1.1 设Aij是F上的mi×nj(i=1，2，…，t:j=1，2，…，w)矩阵，Xj是nj×s(j=1，2，…，w)未×swAX=B知矩阵，Bi是mi(i=1，2，…，t)矩阵，则线性方程组∑ijji(i=1，2，…，t)在F上有解当且仅当

定理4.1.2 设

1)Aij，Xj如定理4.1.1所述，0i是F上的mi×s(i=1，2，…，t)零矩阵; 2)记

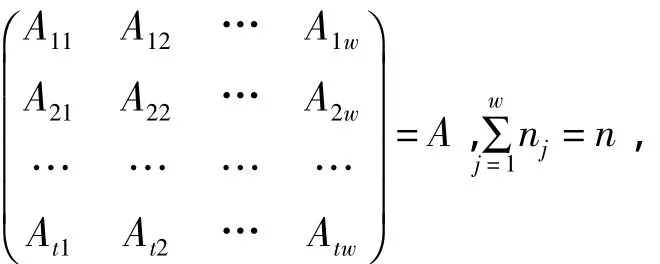
秩(A)=r;

3)当r＜n时，η1，η2，…，ηn－r(列向量)是以A为系数矩阵的齐次线性方程组的一个基础解系;

4)作

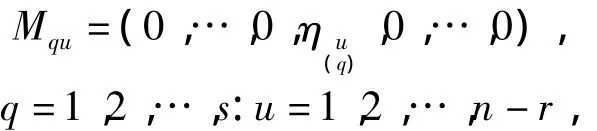
并且将Mqu从第一行开始依次按n1，n2，…，nw行的数目分块而得到一组w个矩阵，仍然以Mqu表示该组的w个矩阵，则

1)线性齐次方程组∑

j=w1AijXj=0i(i=1，2，…，t)的一切解构成线性空间Fn×s的一个子空间;

2)当r＜n时，Mqu(q=1，2，…，s:u=1，2，…，n－r)是子空间的一个基，从而是(n－r)s维子空间，它的一切都是，其中aqu取遍F的一切元素，并且将组合得到的矩阵从第一行开始依次按n1，

［4］讨论了p2k元域中的一个n元pk+1次齐次方程的解的个数，给出了下面的

定理4.1.4 p2k元域中的n元pk+1次齐次方程x2pk+x2pk+1+…+xpnk+1=1在该域中有((pk)n－(－1)n)(pk)n－1个非零解，其中1表示域的单位元.

4.2 方程的求根公式

方程的求根公式就是用方程的系数表示其根的式子.在比较久远的古代，二次方程的求根公式就已经被埃及和巴比伦的先民们发现并记载.在16世纪的一段时间里，寻找三次方程的求根公式成为意大利数学家们的热门问题，并流传下来一些动人的故事，求根公式终于被找到，从而促使人们向着四次和更高次的方程挺进，促进了代数学的发展，奠定了近代数学产生的直接基础.对于有限域上的方程，同样存在求根公式的问题.

对于2k元域F上的二次方程，笔者曾就一种情况得到根的表示公式，写成［22］，于2001年发表;后来，郑州解放军信息学院王念平进行了研究，写成［23］，于2004年发表;笔者认为，这一问题尚待进一步研究，此处从略.至于三次方程的求根公式，当然也可以考虑.

4.3 本原多项式与本原元素

本段中，p元域记为Fp，对于Fp［x］中的多项式，建立其周期的概念，进而，建立本原多项式的概念.Fp的m次扩域Fpm是Fp的单扩域，若有

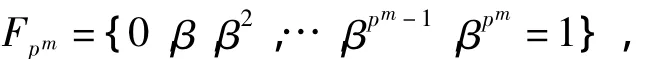
则称β是Fpm的一个本原元素，其中1表示域的单位元.本原多项式是不可约多项式.β是Fpm的一个本原元素当且仅当β是m次本原多项式的根.详细的讨论见［24］.

4.4 n 方元素

［25］给出了n方元素的概念，并进行了讨论;［19］进一步讨论了n方元素，并给出了完全的解决.

5 结束语

从1983年笔者的［26］到2001年笔者的［27］，其间的十几年笔者与其他代数学同行一起，解决了pk元域F上的二次方程和三次方程的问题，笔者的［28］对此作了总结.

笔者的［29］－［35］讨论了pk元域及其单超越扩域上的二项方程、三项方程、因式方程，［36］对此作了总结.

应该指出，还有一些问题有待进一步研究，本文所列的文献中就提出了一些问题，另外，组合设计等有的学科也将不断推动这方面的研究.n2，…，nw行的数目分块而得到一组w个矩阵，仍然以Mqu表示该组的w个矩阵，分别作为X1，X2，…，Xw所取的矩阵，称Mqu(q=1，2，…，s:u=1，2，…，n－r)为一个基础解系;

3)解的个数为pks(n－r).

定理4.1.3 设Aij，Xj，Bi，0i如定理4.1.1和定理4.1.2所述，N是

的一个特解，则

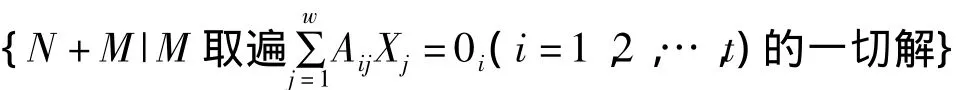
是其解的集合，其中N与M均取定理4.1.2中的那种分块形式.

［1］熊全淹.近世代数［M］.上海:上海科学技术出版社，1978.

［2］张禾瑞.近世代数基础［M］.北京:高等教育出版社，1978.

［3］孙宗明.p2m元域上的某些方程的解的状况［J］.吉安师专自然科学学报，1986，(2):34－36.

［4］孙宗明，等.pk元域上的方程xq+1=λ与x+xq=μ［J］.山东师范大学学报(自然科学版)，1994，(2):11－13.

［5］孙宗明.pk元域上的方程xps－x－c=0［J］.周口师范学院学报，2011，(5):1－3.

［6］孙宗明.pk元域上一元方程的几个降次定量［J］.山东教育学院学报，1991，(2):31－33.

［7］孙宗明.有限域上二项方程根的求法［J］.山东教育学院学报，1989，(4):36－39.

［8］孙宗明，等.关于pk元域上的二项方程［J］.泰安师专学报(自然科学版)，1994，(2):17－21.

［9］万哲先.代数与编码［M］.北京:科学出版社，1976.

［10］孙宗明.pk元域上不可约多项式［J］.山东教育学院学报，1993，(2):40－42.

［11］孙宗明，等.关于一元多项式未定元的替换［J］.聊城师范学院学报，1997，(2):28－30.

［12］孙宗明.有限域上的不可约多项式的存在性与求法［J］.开封大学学报，1993，(3):16－19.

［13］孙宗明.域Fp与Fq上的m次不可约多项式［J］.殷都学刊(自然科学版)，1993，(4):38－41.

［14］孙宗明.pk元域的m次不可约多项式与xpkm－x的因式分解［J］.泰安师专学报(自然科学版)，1995，(2):9－12.

［15］孙宗明.p元域上的一类不可约多项式［J］.殷都学刊(自然科学版)，1990，(1):22－23.

［16］孙宗明.有限域上的不可约多项式的根的注记［J］.临沂师专学报(自然科学版)，1991，(1):11－13.

［17］孙宗明.有限域上的不可约多项式的根号解［J］.内蒙古师大学报(自然科学版)，1995，(2):12－15.

［18］孙宗明.有限循环群的若干特征性质［J］.曲阜师院学报(自然科学版)，1982，(3):50－54.

［19］孙宗明.pk元域中元素的n次根［J］.周口师范学院学报，2011，(2):16－19.

［20］孙宗明.pk元域上线性矩阵方程(组)的理论［J］.周口师范学院学报，2008，(2):19－20，26.

［21］孙宗明.线性矩阵方程(组)的理论［J］.益阳师专学报，1993，(6):25－30(美国，Math.Riews，1994年索引).

［22］孙宗明.2k元域上的二次方程根的公式［J］.数学的实践与认识，2001，(6):132－133(美国，Math.Riews，2002年索引).

［23］王念平.关于“2k元域上的二次方程根的公式”的注记［J］.数学的实践与认识，2004，(11):148－152.

［24］孙宗明.F［x］中的本原多项式与GF(pn)中的本原元素［J］.泰安师专学报(自然科学版)，1990，(1):1－5.

［25］孙宗明，等.pk元域上的n方元素［J］.广西师范学院学报(自然科学版)，1995，(增刊):6－8.

［26］孙宗明.pk(p≥3)元域上的二次方程的根的状况［J］.数学的实践与认识，1983，(4):29－31(美国，Math.Riews，85i:11104).

［27］孙宗明.pk元域上的三次方程根的状况［J］.内蒙古师大学报(自然科学汉文版)，2001，(3):28－31.

［28］孙宗明.pk元域上的二次方程与三次方程［J］.泰山学院学报，2011，(3):8－16.

［29］孙宗明.pk元域上的方程xq=d与ax2q+bxq+c=0［J］.内蒙古师大学报(自然科学汉文版)，1990，(1):22－26(美国，Math.Riews，92h:11110).

［30］孙宗明.pk元域上的二项方程和三项方程根的状况［J］.内蒙古师大学报(自然科学汉文版)，1991，(3):20－24(美国，Math.Riews，96 f:12001).

［31］孙宗明.pk元域F的单超越扩域E上的方程yn=D与Ay2n+Byn+C=0［J］.内蒙古师大学报(自然科学汉文版)，2000，(3):9－12.

［32］孙宗明.pk元域上的一类方程根的状况［J］.河北师范大学学报(自然科学版)，1996，(2):23－35.

［33］孙宗明.2k元域上的方程∑(－1)iaixn－1－i=0［J］.山东科技大学学报(自然科学版)，2001，(1):10－12(美国，Math.Riews，2002b:11172).

［34］孙宗明.pk元域上的方程∑aixn－1－i=0与∑(－a)ixn－1－i=0［J］.商丘师范学院学报，2005，(2):57－59.

［35］孙宗明.pk元域F的单超越扩域E上的方程∑Aixn－1－i=0与∑(－A)ixn－1－i=0［J］.集美大学学报(自然科学版)，2007，(2):129－132.

［36］孙宗明.pk元域及其单超越扩域上的二项方程三项方程和因式方程［J］.内蒙古师大学报(自然科学汉文版)，2011，(5):21－26.