双圆弧谐波齿轮传动基本齿廓设计
辛洪兵
北京工商大学,北京,100048
双圆弧谐波齿轮传动基本齿廓设计
辛洪兵
北京工商大学,北京,100048
在研究圆弧齿廓谐波齿轮传动啮合原理的基础上,提出了双圆弧谐波齿轮传动柔轮和刚轮基本齿廓设计方法。该基本齿廓可以保证啮合过程中,柔轮和刚轮齿廓始终处于共轭运动状态,特别在啮合过程中,存在柔轮凸齿廓和凹齿廓分别与刚轮凹齿廓和凸齿廓同时处于共轭运动的“双共轭”啮合区间,这对于提高双圆弧谐波齿轮传动扭转刚度和传动精度具有重要作用。开发了椭圆凸轮波发生器双圆弧谐波齿轮传动基本齿廓,根据该齿廓设计制造了双圆弧谐波齿轮滚齿刀、双圆弧谐波齿轮插齿刀和双圆弧谐波齿轮传动样机。对比分析与实验表明,与渐开线齿廓相比,双圆弧齿廓谐波齿轮传动的柔轮强度、传动精度和扭转刚度等明显提高。
双圆弧齿廓;谐波齿轮传动;齿轮刀具;基本齿廓
1 研究背景
谐波齿轮传动装置具有体积小、传动比大、效率高、精度高等优点,是重要的精密传动部件。目前约有90%的谐波齿轮传动装置应用在机器人工业和精密定位系统中[1]。
1926年 Wildhaber提出法面为圆弧齿廓的斜齿轮[2],该齿轮的凹齿齿廓圆心在齿条型刀具的节线上,但是由于强度问题,没有应用于工业生产。1956年,Новиков发明了端面为圆弧的圆弧齿轮[2],该齿轮法面齿廓为圆弧,凸齿齿廓圆心在齿条型刀具的节线上,制造方便。W ildhaber齿轮的齿廓和 Новиков齿轮的齿廓非常接近,国际上统称为W-N齿轮。对于一般齿轮传动,圆弧齿轮具有三个主要优点:能承担3~4倍相同尺寸渐开线齿轮的载荷;提高渐开线齿轮承载能力的措施可以用于圆弧齿轮;圆弧齿轮齿面容易形成油膜。为保证连续传动,圆弧齿轮采用斜齿传动[2]。
目前,我国在生产中采用的圆弧齿形有[3]:单圆弧齿廓、公切线式双圆弧齿廓和分阶式双圆弧齿廓。
在谐波齿轮传动中采用双圆弧齿廓,可以有效地改善柔轮齿根的应力状况和传动啮合质量,减小体积,提高承载能力和扭转刚度,减小最小传动比,提高传动系统动态性能。但是谐波齿轮传动不能移植普通圆弧齿轮的上述齿廓,而必须以谐波齿轮传动啮合原理为基础,设计满足谐波传动要求的全新双圆弧齿形。具有不同波发生器的谐波齿轮传动,其双圆弧齿廓也不相同[4-5]。
20世纪后期,日本基于余弦凸轮波发生器开发了近似共轭、具有S形齿形(即双圆弧齿形)的圆弧齿廓谐波齿轮,经过不断完善[6-10],已将其成功应用于机器人等多种领域,用于减小体积和提高系统动态特性,基于该齿形,日本实现了传统谐波齿轮传动的升级换代[11]。
日本基于余弦凸轮波发生器开发的双圆弧谐波齿轮传动产品目前已垄断国际市场。国内机器人产业需要的高性能双圆弧谐波齿轮传动产品全部依赖进口。双圆弧齿廓谐波齿轮传动装置在柔轮疲劳寿命和扭转刚度上比现有渐开线齿廓谐波齿轮传动装置提高50%[11]。通过应用双圆弧齿廓,可以进一步减小具有杯形柔轮的谐波齿轮传动装置的轴向尺寸,还可以获得更小的传动比,因而它除易于提高应用系统的动态特性外,更主要的是能大幅度扩大谐波齿轮传动的应用范围,在工业上具有巨大的市场潜力和广阔的应用前景。因此,研究具有自主知识产权的双圆弧谐波齿轮传动装置,对于国内谐波传动技术发展和满足高性能谐波传动产品需求具有重要作用。
因为不可能通过圆弧齿轮的变位来适应不同形式的波发生器和柔轮径向变形量系数,以改善齿轮的啮合性能,所以从减少圆弧齿轮加工的刀具数目出发,在开发圆弧谐波齿轮传动基准齿形以前,必须限定波发生器形式和柔轮径向变形量系数[4-5]。前苏联对四滚子波发生器,限定其滚子夹角 β=25°和 β=35°[8],而日本则选用余弦凸轮波发生器[9-10]。
前苏联提出的基于四滚子波发生器的谐波齿轮传动柔轮和刚轮的圆弧齿形分别如图1和图2所示[12]。图2表明,前苏联的刚轮齿形不是双圆弧,而是由单圆弧和直线组合而成。该齿形方案存在的问题是,在整个啮合过程中,刚轮与柔轮齿形不是严格共轭运动,轮齿在啮合区接触比小,加工中需要的刀具数目多。目前(如文献[13]等)进行的双圆弧齿形啮合性能研究都是针对上述前苏联齿形进行的。
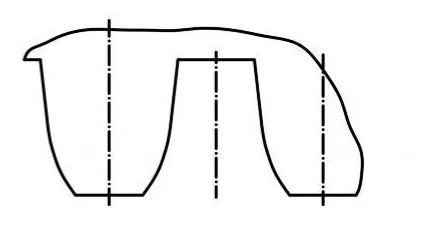
图2 前苏联提出的刚轮圆弧齿形

图1 前苏联提出的柔轮圆弧齿形
日本基于余弦凸轮波发生器提出的双圆弧谐波齿轮传动齿形如图3所示[6,8],该齿形是在未考虑柔轮与刚轮相对运动过程中柔轮中性线法线转动的情况下的近似设计。由于柔轮中性线法线的转动角度是谐
波齿轮传动共轭运动的重要参数,所以,这种近似设计导致所谓S形齿形谐波齿轮传动中柔轮齿与刚轮齿之间相对运动不是共轭运动,传动中存在齿廓干涉现象。该缺陷在随后的研究中逐渐被改善[8-9]。
国内谐波齿轮传动主要采用椭圆波发生器,上述前苏联和日本开发的谐波齿轮圆弧齿廓不能用于具有椭圆波发生器的谐波齿轮传动。为开发具有自主知识产权的双圆弧谐波齿轮传动技术,本文根据谐波齿轮传动啮合原理和国内谐波齿轮传动产品生产的主要工艺特点,进行椭圆波凸轮波发生器双圆弧谐波齿轮传动基本齿廓设计。

图3 日本提出的双圆弧齿形
2 谐波齿轮传动双圆弧齿廓设计
不同于一般齿轮传动,对渐开线齿廓谐波传动的啮合分析表明,其共轭运动只发生在长轴附近很窄的角度范围内,即距长轴约5°和33°附近有二个共轭区域,对于内波谐波齿轮传动,柔轮与刚轮齿廓只在距长轴5°附近一个很窄区间内实现了共轭运动。但是柔轮齿从刚轮齿槽中完全脱出,发生器需要转过45°到 60°,即柔轮齿顶从刚轮齿槽中脱离刚轮齿顶时,波发生器转角约在45°至60°范围内。这样,在5°附近的窄区间之外,柔轮与刚轮齿的相对运动理论上是不接触的,这一特点在渐开线齿廓谐波齿轮传动侧隙图上可清楚地表现出来。尽管当载荷逐渐增大时,由于柔性轴承与柔轮等的弹性变形,会有较多的柔轮齿与刚轮齿进入尖点啮合,但是这种啮合特性会导致在小载荷情况下,具有渐开线齿廓谐波齿轮传动的轮齿接触对数少,扭转刚度较低,降低了谐波齿轮传动的动态性能。渐开线齿廓谐波齿轮传动的这种相对运动特点可称之为“有限共轭运动”,其特点是在轮齿的整个相对运动过程中,只有很小的啮合区内存在共轭运动,而在其他位置齿廓并不接触。
对具有单圆弧齿的圆弧齿廓谐波齿轮传动理论的啮合计算表明,在从0°开始的一个很宽的区间内,都有共轭齿廓存在[4-5]。这说明,不同于渐开线齿廓谐波传动的“有限共轭运动”,在圆弧齿廓谐波齿轮传动轮齿的整个啮合过程中,轮齿之间始终处于共轭运动状态,这使柔轮和刚轮齿廓在整个啮合弧上保持共轭接触,同时啮合的齿对数增加,扭转刚度和传动精度得到提高。与渐开线谐波传动相比,由于圆弧齿廓谐波齿轮分担载荷的啮合齿对增加,使得作用到柔轮和柔性轴承上的载荷分布均匀,柔轮和柔性轴承的寿命得到提高,另外,由于圆弧齿形的齿根过渡圆角半径较大,柔轮的强度得到进一步提高。
由于谐波传动原理不同于一般的齿轮传动,所以圆弧齿廓谐波齿轮传动的齿形受到啮合参数、结构参数、柔轮变形形状以及传动比等诸多因素的约束,要对圆弧齿廓谐波齿轮传动开展研究,首先就需要在这一问题中取得突破。
2.1 主要齿形参数的确定
2.1.1 齿高和啮合深度
对具有渐开线齿廓的双波二齿差椭圆波发生器谐波齿轮传动啮合深度等参数进行的分析表明:由于柔轮齿顶和刚轮齿廓会产生干涉,二者的啮合深度并非理论齿高h=2m(m为模数),而是小于此值的hd1,啮合深度hd1约在1.2m ~1.3m范围。对于四齿差传动,由于柔轮的变形量系数的增大(Δ1=2),柔轮齿与刚轮齿的啮合深度可以达到2m而不发生干涉。但与其对应的两齿差谐波齿轮传动相比,由于后者模数只有前者的一半,因此啮合深度的绝对值并没有明显变化。
对于渐开线齿廓,解决齿廓干涉的方案有两个,即采用分别去除部分齿顶高的方式,将柔轮和刚轮轮齿的干涉部分去处,同时保持一定的齿顶啮入侧隙;或者采用大变位系数的方法,利用大变位情况下齿顶变尖去除二者齿顶的干涉部分。
全齿高、名义压力角、齿廓圆弧半径是决定圆弧齿形的三个主要参数。圆弧齿廓谐波齿轮传动齿形参数必须根据谐波传动的啮合特点设计,而且齿形不能发生干涉,并保持一定的啮入间隙j n。
根据圆弧齿廓谐波齿轮传动啮合原理分析,圆弧齿廓谐波齿轮传动不须采用螺旋齿轮,只用直齿圆弧齿轮就可以实现连续传动。因此在以后的计算分析中,端面模数m等同于法向模数mn,除非特别说明。
参考一般圆弧齿轮设计经验,对于精滚调质的软齿面圆弧齿轮,一般取全齿高h为2m~2.25m,考虑到谐波齿轮传动包角的限制,柔轮齿与刚轮齿之间需要保留一定的顶隙和啮入间隙。双圆弧齿廓谐波齿轮传动柔轮基准齿形齿高h可初步定为1.8m~2.2m,柔轮齿顶高h a可以取为0.7m ~1.0m,齿根高hf为1.1m ~1.5m,取齿顶间隙C a为0.2m~0.35m。
2.1.2 啮合角
谐波齿轮传动的齿形角是在给定参数(如波发生器型式、柔轮中性圆半径、柔轮壁厚、柔轮的径向变形量系数以及传动比等)的情况下,由柔轮齿相对于刚轮齿的运动轨迹所决定的。对具有渐开线齿廓的谐波传动的分析表明,在通常使用范围内,平均齿形角在25°左右,而渐开线齿廓变位的主要任务就是调整齿形角以避免齿廓干涉,改善啮合质量。由于柔轮与刚轮轮齿的相对运动轨迹不受齿廓型式的影响,因此不管采用什么齿廓,都必须满足上述齿形角要求,以免产生齿廓干涉。而圆弧齿廓不能变位,因此在齿形设计中,根据谐波齿轮传动特点,谐波传动圆弧齿廓的名义压力角 α0取为25°。
2.1.3 齿廓圆弧半径差
凸齿廓、凹齿廓的半径差Δρ的值应根据制造齿轮的经济精度确定,对于软齿面中小模数齿轮,凹齿的齿廓半径比凸齿的圆弧齿廓半径增大10%左右,即Δρ=0.1ρa(ρa为柔轮右侧凸齿廓圆弧半径),随着加工精度的不断提高,可以逐步减小 Δρ。
采用增加半径差Δρ的方式可以使轮齿磨合后增加接触面积,提高抗点蚀强度,考虑到谐波齿轮传动多齿对啮合的特性,凸齿廓、凹齿廓半径差Δρ的大小对谐波齿轮传动的影响效果还有待实践验证。
由于谐波齿轮传动具有多齿对啮合的特点,齿面比压小,设计中忽略柔轮凸齿廓和刚轮凹齿廓之间半径差Δρ。凸齿廓、凹齿廓具体的半径大小由圆弧拟合确定。
2.1.4 齿厚比
齿厚比K是节圆上齿槽宽度sf与齿厚sa的比值,即 K=s f/s a。
齿厚比的大小主要影响分阶式双圆弧轮齿的弯曲强度,根据国内对一般圆弧齿轮的实践经验,一般都取K为1.1~1.3,由于谐波齿轮传动的多齿对啮合特性,轮齿弯曲强度不是生产实践中的主要问题,相反,柔轮齿根圆弧半径以及齿高厚度比是决定柔轮寿命的重要因素。因此,从增大柔轮齿槽宽、减小柔轮齿圈的弯曲刚度的角度出发,K应取较大数值,同时,柔轮齿根圆角半径也应尽量取较大数值,否则会影响柔轮的强度和承载能力。对于采用公切线式双圆弧齿廓的谐波齿轮传动,齿厚比K应取较大值,如K=1.3。
2.1.5 齿侧间隙
由于不能像渐开线齿轮那样通过刀具径向变位来增大切深以获得侧隙,否则圆弧齿廓的名义接触点就会偏移,因此传动所必须的侧隙规定在基本齿廓中,对于一般圆弧齿轮传动,侧向间隙j1为0.04m~0.06m,对于普通小模数圆弧齿轮传动,侧隙可以取较大值。考虑到谐波齿轮传动的设计与生产实际,侧向间隙可确定为0.01m~0.02m。
2.1.6 啮入间隙
由谐波齿轮传动的啮合运动特点,轮齿在啮入时需要有一定的啮入间隙j2,否则容易导致齿顶发生干涉,对于渐开线谐波齿轮传动,伊万诺夫[12]的建议值为0.1k z m ~0.13k z m,其中,k z为齿差系数,对于双波两齿差传动,k z=1。
根据上述参数选择,初步确定全齿高 h为1.8m ~2.2m,柔轮齿顶高ha为0.7m ~1.0m,齿根高h f为1.1m ~ 1.5m,齿顶间隙C a为0.2m ~0.35m,名义压力角 α0=25°,齿厚比 K=1.3,齿侧间隙 j1为 0.01m ~0.02m,啮入间隙 j2为0.1m~0.13m。
2.2 柔轮变形形状
针对目前的工艺实际,确定双圆弧谐波齿轮传动采用椭圆波发生器。柔性轴承的内外圈和柔轮啮合齿圈中截面在椭圆波发生器的作用下,理论上都成为椭圆波发生器外廓线的等距曲线。

式中,r为柔轮中性圆半径。
2.3 椭圆波发生器啮合不变矩阵中的元素
利用改进运动学方法建立的啮合不变矩阵在谐波齿轮传动啮合原理的研究中具有如下重要特点:对某一特定的变形形状(波发生器型式),可以生成一个只包含运动参数的矩阵,这个矩阵当柔轮或刚轮采用不同齿廓时具有不变性[14]。这样,可以将描述柔轮复杂运动规律的运动参数只包含在啮合不变矩阵中,当柔轮采用各种形状的齿形时,只需输入其齿形方程和法线方程,不须重复求解大量的偏导数,而只需调用同一个矩阵,就可以对柔轮的共轭齿廓进行计算分析。
改变柔轮变形形状时,只需根据波发生器型式推导新的啮合不变矩阵。推导出椭圆波发生器径向位移w(φ)、切向位移v(φ)和法向转角 μ(φ)以及d w/dφ、d v/dφ和dμ/dφ的计算公式,再将它们代入啮合方程中的啮合不变矩阵,即可分析具有不同齿廓的椭圆凸轮波发生器谐波齿轮传动啮合理论。
2.4 谐波齿轮传动柔轮双圆弧齿形方程
2.4.1 柔轮凸齿圆心移距量X a和偏移量l a
如图4所示,柔轮凸齿圆心移距量Xa为

2.4.2 柔轮凸齿廓方程
如图5所示,d1为柔轮节圆直径,d n为柔轮内径,do为柔轮中性圆直径。在柔轮轮齿坐标系中,
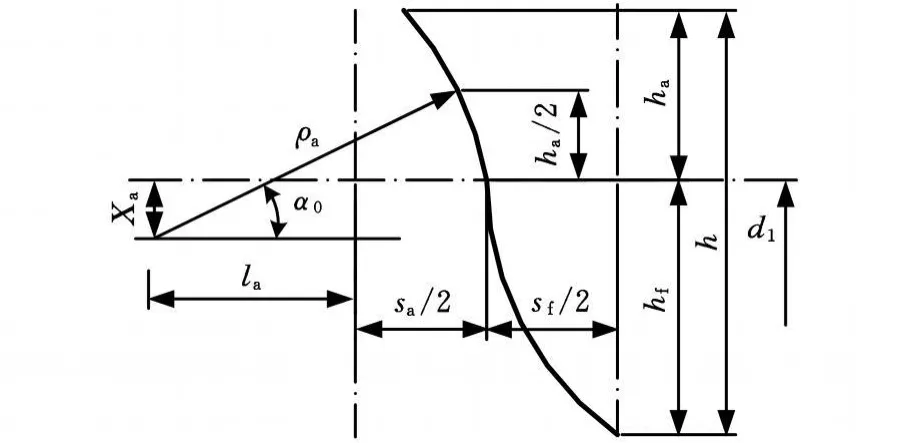
图4 柔轮右侧凸齿廓
柔轮右侧凸齿廓方程为

式中,ua为柔轮右侧凸齿廓沿Z1方向的拓展参数;αa为凸齿廓上M点的压力角;t为柔轮壁厚;(xoa,yoa)为柔轮右侧凸齿廓圆心坐标。

图5 柔轮轮齿坐标系
2.4.3 柔轮凹齿廓方程
在柔轮轮齿坐标系中,柔轮右侧凹齿廓方程为

式中,Xf与lf分别为柔轮凹齿圆心移距量和偏移量;αf为凹齿廓压力角;ρf为柔轮凹齿圆弧半径;uf为柔轮右侧凹齿廓沿Z1方向的拓展参数。
将式(1)与式(2)代入谐波齿轮传动的啮合基本方程[14],可以求出与柔轮凸齿廓共轭的刚轮齿廓。将式(3)与式(4)代入谐波齿轮传动的啮合基本方程[14],可以求出与柔轮凹齿廓共轭的刚轮齿廓。
柔轮凸齿圆心移距量X a、偏移量l a、圆弧半径ρa及柔轮凹齿圆心移距量 Xf、偏移量 lf、圆弧半径ρf采用优化方法在谐波齿轮传动啮合原理的基础上求解。
3 双圆弧齿形设计过程
在椭圆凸轮波发生器作用下,同一条凸齿圆弧齿廓会在整个啮合区的两个区域内形成两条理论共轭齿廓,该两个区域分别标记为 ⅠS11区域和ⅡS11区域,两条理论共轭齿廓分别记为S21和S22。研究结果表明,用圆弧可以很好地拟合理论共轭齿廓S21,由圆弧拟合造成的齿形误差小于实际制造公差要求,因此,S21的拟合圆弧可以作为刚轮的凹齿廓。
刚轮凸齿廓可以采用柔轮凸齿廓的第二条理论共轭曲线S22的拟合圆弧。但是,柔轮凹齿廓S12的设计必须保证其理论共轭齿廓S′22与柔轮凸齿廓的第二条理论共轭齿廓S22相一致,否则,在谐波齿轮传动的啮合过程中,柔轮凹齿廓S12就会与刚轮凸齿廓发生干涉,如图6所示。

图6 柔轮凹齿廓S12须保证其理论共轭齿廓S′22与柔轮凸齿廓的第二条理论共轭齿廓S22相一致
根据以上分析,如图7所示,双圆弧谐波齿轮传动共轭齿廓的的设计采用以下过程:首先以保证提高柔轮强度为目标,设计柔轮的凸齿廓S11和凹齿廓S12;其次根据谐波传动啮合原理设计求解凸齿廓S11的理论共轭齿廓S21和S22,对S21用最优圆弧进行拟合,确定拟合圆弧的圆心和半径等参数,以此作为刚轮圆弧凹齿廓的设计基础;然后根据谐波传动啮合原理设计求解柔轮凹齿廓S12的理论共轭齿廓S23,检验S23是否与S22干涉,确保S23与S22相一致,以使柔轮在刚轮齿槽的啮入啮出过程中,齿廓始终处于共轭运动状态;最后完善并完成柔轮与刚轮双圆弧齿形的设计。

图7 双圆弧谐波齿轮传动共轭齿廓的设计过程
以上设计过程都在用改进运动学方法建立的谐波齿轮传动啮合原理研究的啮合不变矩阵法[14]的基础上进行的。
4 双圆弧谐波齿轮传动基本齿廓
采用椭圆凸轮波发生器的谐波齿轮传动的啮合原理分析涉及椭圆积分运算,不能期望得到圆弧齿廓的精确解析表达式,因此采用椭圆波发生器的双圆弧齿廓谐波齿轮传动的共轭齿廓的设计都采用数值计算方法。齿形拟合误差数量级为10-6mm,拟合精度满足工程实际要求。
所设计的双圆弧谐波齿轮传动柔轮基本齿廓如图8所示,刚轮基本齿廓如图9所示。

图8 双圆弧谐波齿轮传动柔轮基本齿廓

图9 双圆弧谐波齿轮传动刚轮基本齿廓
具有椭圆波发生器的双圆弧谐波齿轮传动符合国内谐波齿轮传动产品生产工艺特点,工艺性能优良,特别是它不同于日俄技术方案,具有完全自主知识产权[15-17]。该基本齿廓可以保证柔轮在刚轮齿槽的啮入啮出过程中,齿廓始终处于共轭运动状态,特别在啮合过程中,在ⅠS11区域,存在一段柔轮凸齿廓和凹齿廓分别与刚轮凹齿廓和凸齿廓同时处于共轭运动的“双共轭”啮合区间。双圆弧谐波齿轮传动存在的“双共轭”啮合情况与一般双圆弧齿轮传动有本质不同。首先,由于啮合原理不同,采用双圆弧齿廓的谐波齿轮传动,其轮齿只需直齿即可满足连续传动要求[4],并且,在垂直齿轮轴线的同一端面上,相对于波发生器长轴一定角度范围内,同侧齿廓上凸齿廓接触点与凹齿廓接触点同时存在,其轴向距离为0,在该角度范围内,同侧齿廓上凸齿廓与凹齿廓同时处于共轭啮合状态。从啮入侧来看,该角度为柔轮凹齿廓进入啮合到结束啮合所对应的波发生器转角。齿宽受承载能力约束,毋需普通双圆弧齿轮传动保证齿轮连续传动的约束条件。以上接触点均为齿廓共轭点,这又不同于渐开线谐波传动中存在大量尖点啮合的情况。这种啮合特点对于提高双圆弧谐波齿轮传动扭转刚度和传动精度具有重要作用。
5 试验研究
根据双圆弧齿廓谐波齿轮传动柔轮和刚轮基本齿廓,设计制造了模数m分别为0.5mm、0.6mm、0.7mm、0.8mm 、1.0mm 的用于加工柔轮的双圆弧滚齿刀和加工刚轮的双圆弧插齿刀。其中模数m为1.0mm的双圆弧滚齿刀和双圆弧插齿刀分别如图10和图11所示。

图11 双圆弧谐波齿轮插齿刀实物

图10 双圆弧谐波齿轮滚齿刀实物
图12为模数m=1.0mm、传动比i=100,具有椭圆凸轮波发生器的双圆弧谐波齿轮传动样机。

图12 双圆弧谐波齿轮传动样机
完成了小模数双圆弧谐波齿轮传动样机设计、制造和性能测试等任务,实验结果证明了双圆弧谐波齿轮传动在传动精度和扭转刚度方面的优越性。有限元分析结果表明,在相同条件下,具有双圆弧齿廓的柔轮齿根最大应力可比渐开线齿廓减小25.52%,双圆弧齿形可以作为减小柔轮应力即提高谐波传动承载能力的重要技术手段。
对双圆弧谐波齿轮传动样机与渐开线谐波齿轮传动对照试验样机进行的传动精度试验表明,在相同条件下,双圆弧谐波齿轮传动的运动精度比渐开线谐波齿轮传动高24.27%。
如图13所示,对双圆弧谐波齿轮传动样机与渐开线谐波齿轮传动对照试验样机进行的扭转刚度试验表明,在卸载段,随着负载扭矩的减小,双圆弧谐波齿轮传动的扭转刚度比渐开线谐波齿轮传动增加28%~66%,在加载段,随着负载扭矩的增大,双圆弧谐波齿轮传动的扭转刚度比渐开线谐波齿轮传动增加20%~42%。这表明,双圆弧谐波齿轮传动的扭转刚度比渐开线谐波齿轮传动至少增加 20%。在小负载范围内,至少增加42%,特别在卸载段,可达60%以上。采用双圆弧谐波齿轮传动,可以提高谐波齿轮传动系统的动态性能。
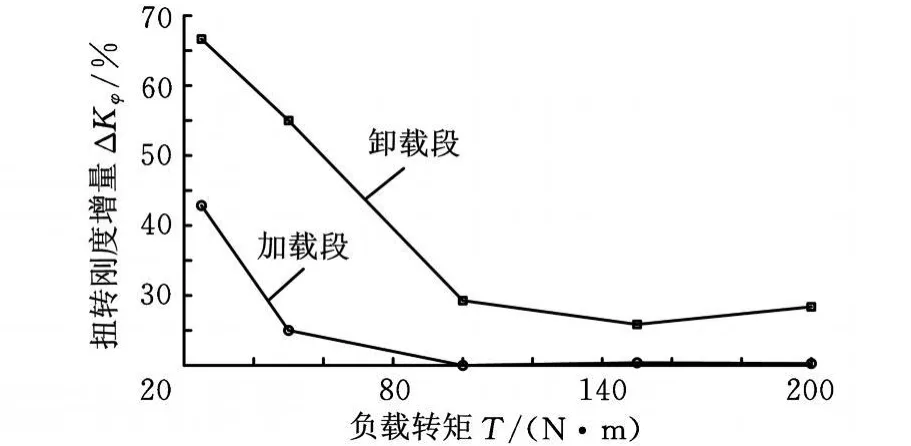
图13 扭转刚度增量ΔK 与负载转矩T的关系
[1] Popov P K.Preparation for Manufacturing of New Generation H armonic D rive in Russia[J].Gearing and Transm issions,1996(1):33-40.
[2] 邵家辉.圆弧齿轮[M].北京:机械工业出版社,1994.
[3] 齿轮手册编委会.齿轮手册[M].北京:机械工业出版社,1990.
[4] 辛洪兵.圆弧齿廓谐波齿轮传动齿形设计中的几个问题[J].机械传动,1999,23(2):11-12.
[5] 辛洪兵,何惠阳,谢金瑞.精密谐波齿轮传动采用圆弧齿廓的合理性证明[J].长春光学精密机械学院学报,1997,20(3):47-50.
[6] Shochi I.Tooth Profile of Spline of Strain Wave Gearing:US,4823638[P].1989-04-25.
[7] Yoshihide K,Noburu T,Takahiro O,et al.Cuptype H armonic D rive Having a Short,Flexib le Cup Member:US,5269202[P].1993-12-14.
[8] Aubin J J.Tooth Pro file A rrangement to Elim inate Tooth Inter ference in Ex tended Contact Harmonic Drive Devices:US,5456139[P].1995-10-10.
[9] Aubin J J,Komori E,Yamada Y.Harmonic D rive Devices,and a Method o f Generating Tooth Profiles Therefore:European,EP 0767325 A 2[P].1997-09-04.
[10] Shoichi I.Strain Wave Gearing Having a Non Interfering W ide Mesh Range Tooth Profile:US,5918508[P].1999-07-06.
[11] Harmonic Drive LLC.The"S"Series Tooth Form[EB/OL].[2010-05-11].http://www.harmonicd rive.net/reference/advantages/stooth.php.
[12] 伊万诺夫M H.谐波齿轮传动[M].沈允文,李克美,译.北京:国防工业出版社,1987.
[13] 曾世强,杨家军,王宣福.双圆弧齿形谐波齿轮传动的运动特性分析[J].华中理工大学学报,2000,28(1):12-14.
[14] 辛洪兵.研究谐波齿轮传动啮合原理的一种新方法[J].中国机械工程,2002,13(3):181-183.
[15] 辛洪兵.双圆弧谐波齿轮滚齿刀:中国,ZL200610112756.0[P].2008-03-05.
[16] 辛洪兵.双圆弧谐波齿轮插齿刀:中国,ZL 200610112754.1[P].2008-03-05.
[17] 辛洪兵.具有双圆弧齿廓的谐波齿轮传动:中国,ZL 200610112755.6[P].2008-03-05.
Design for Basic Rack of Harmonic Drivewith Double-circular-arc Tooth Profile
Xin Hongbing
Beijing Technology and Business University,Beijing,100048
On the basis of research on engagem ent p rincip le of harm onic d rive with circu lar-arc tooth p rofile,a design m ethod was p resented for doub le circular-arc tooth p rofile of basic rack for flexsp line and rigid sp line of harmonic drive.The doub le circular-arc tooth profiles o f basic rack ensured the tooth pro files of flexsp line and rigid sp line to keep on con jugating w ith each other during the meshing period,especially there existed so-called dual-con jugatedmeshing zones,in w hich the convex and concave pro files of flexsp line con jugated w ith the concave and convex pro files of rigid sp line simutaneously,this characteristics p layed important roles in improving the torsional stiffness and transm ission accuracy of the harmonic drive.The double-circular-arc tooth profiles of basic rack of harm onic drivew ith ellip ticalw avegeneratorwere developed and applied in design andm anufacture of the hobs w ith double-circular-arc tooth profile for flexspline,the shaping cutters with double-circular-arc tooth profile for rigid spline and the samp le device for experimentation.Compared w ith the involute profile,the flexible strength,transmission accuracy,and torsional stiffness of the harmonic drivew ith double-circular-arc tooth profiles aremarked ly improved.
double-circular-arc tooth profile;harmonic drive;wheel cutter;basic rack
TH 132.43;TG721
1004—132X(2011)06—0656—07
2010—03—04
北京市自然科学基金资助项目(3082005)
(编辑 苏卫国)
辛洪兵,男,1968年生。北京工商大学机械工程学院教授。研究方向为谐波齿轮传动及机器人机械学等。获国家发明专利授权5项。出版专著2部,发表论文60余篇。

