非完整约束AGV轨迹跟踪的非线性预测控制
赵 韩 尹晓红 吴焱明
合肥工业大学,合肥,230009
非完整约束AGV轨迹跟踪的非线性预测控制
赵 韩 尹晓红 吴焱明
合肥工业大学,合肥,230009
针对存在非完整约束和控制输入约束的三轮AGV模型,研究其非线性模型预测控制策略,提出了一种跟踪与镇定统一控制算法。首先由模型预测控制原理产生一个优化控制器,接着设计终端控制器及不变终端域来保证系统的镇定,然后设计状态观测器以进一步提高跟踪精度,最后设计避障控制模块来完善整个控制器功能。该控制算法具有一般性,对所有AGV及其他轮式移动机器人的运动学模型都适用。计算机仿真结果验证了该控制算法的正确性和有效性。
AGV;模型预测控制;镇定;观测器;轨迹跟踪
0 引言
近年来,自动引导车(automatic guided vehicle,AGV)作为非完整约束轮式移动机器人(wheeled mobile robot,WMR)的一种,由于实际应用的广泛性,其控制问题也得到了国内外学者的关注。机器人的运动控制大致可以分为镇定控制与轨迹跟踪控制两类。作为一种具有非完整约束的典型系统,WMR不满足反馈稳定的Brockett定理的必要条件,因此不能通过连续时不变状态反馈控制方法实现机器人系统的镇定,故从理论而言,设计镇定控制器更具有挑战性。但从实践意义上来说,轨迹跟踪更具有实际应用价值,因为即使对于镇定控制任务,机器人也要沿某条可行轨迹运动到目标点。为了解决WMR的运动控制问题,人们已经提出各种控制方法,包括滑模控制方法[1]、反演控制方法[2]等在内的非线性控制方法,自适应控制方法[3],神经网络控制方法[4],时变反馈控制法[5],非连续反馈控制法[6]等,取得了较好的控制效果。然而,上述传统方法的可调参数与控制性能之间的关系不是很直观,参数整定很费力,且在考虑实际存在控制输入约束或状态约束时,比较难处理。而模型预测控制(model predictive control,M PC)可以克服以上缺陷,模型预测控制利用求惩罚函数的最小化来确定最优控制输入,参数调整容易,且状态约束及控制输入约束可以在优化过程中直接考虑在内,简单明了。模型预测控制亦称为滚动优化控制(receding horizon contro l,RHC),是近年来发展起来的一类新型计算机控制算法,由于它采用模型预测、滚动优化和反馈校正等控制策略,且其处理约束能力强,因而控制效果好,已成功应用于石油、化工、机械等比较复杂且模型不容易精确建立的工业生产过程。但是,由于源于工程控制的预测控制在设计时没有在理论上考虑系统的闭环镇定性,预测控制是在线反复求解开环优化问题,而开环最优不能保证闭环镇定,因此,如何保证预测控制的镇定性成了一个关键问题。
本文在研究AGV系统的非线性模型预测控制问题时,在基本的预测控制原理基础上着重考虑了预测控制的镇定性,设计了终端控制器和终端域,提出一种跟踪与镇定统一的控制策略。同时,考虑到运动过程中总会存在噪声干扰,使得AGV自定位不够准确,影响轨迹跟踪,本文用一个简单的状态观测器对AGV状态进行估计,从而进一步提高控制精度。最后本文还增加了一个避障功能模块,以此来进一步完善整个控制器功能。
1 AGV模型和预测控制模型
以具有非完整约束的三轮移动机器人小车作为控制对象,其前轮既是转向轮又是驱动轮,结构如图1所示。
假设小车当前实际位姿为X=(x,y,θ)T,任意给定的参考位姿为X r=(x r,y r,θr)T,位姿误差X e=(x e,y e,θe)T;当前实际速度 U=(v,ω)T,参考速度Ur=(vr,ωr)T,其中,vr为参考线速度,ωr为参考角速度。图1中,D为后轮轴与中心轴之间的交点,M为小车质心。非完整约束意味着小车的轮子只有纯滚动而无滑动,即,其中d为点D与点M 之间的距离。移动机器人小车的运动学方程如下:
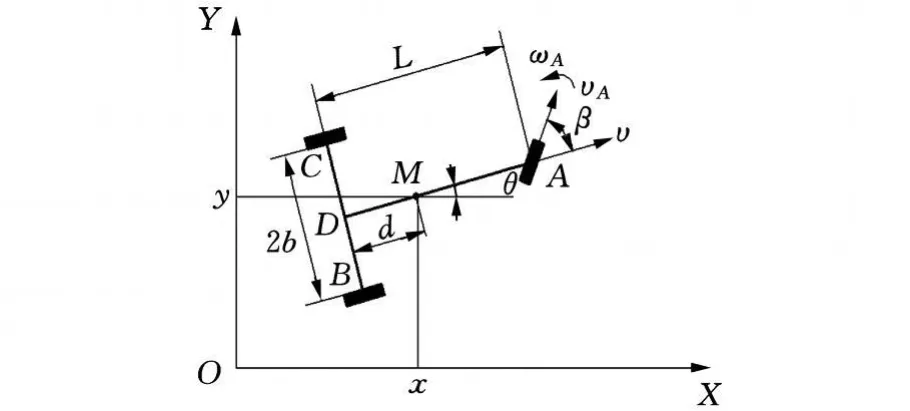
图1 三轮AGV结构示意图

2 轨迹跟踪的模型预测控制算法设计
模型预测控制是一种基于模型的控制,其机理可以描述为:在每个采样时刻,预测模型根据获得的当前系统实际状态信息,在线求解一个有限时域开环最优控制问题,将所得到的控制序列的第一项应用于被控系统,剩余的控制输入丢弃,直至下一采样周期。在下一采样时刻测得系统的实际状态,重复求解优化过程,即所谓的滚动优化。
然而,上述开环的过程并不能保证被控系统的镇定。为了解决这个问题,可以在求解最优问题时在惩罚函数中加入一个终端惩罚函数项以及终端约束,并引入一个终端域的概念。本文的控制思想是把整个控制过程分成两个控制阶段:首先,在有限时域内求解最优控制问题,将获得的最优控制输入到系统,驱动系统使其进入到终端域;然后,利用一个终端线性反馈控制器将系统控制到平衡点。预测控制过程如图2所示,图中,t为当前时刻,Tp为预测时域。
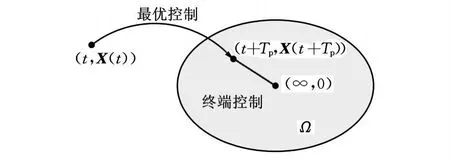
图2 预测控制过程示意图
因此,本文的非线性模型预测跟踪控制思路是:系统给定AGV的参考速度U r和参考位姿X r,它们可以由路径规划算法求得;期望位姿Xr与由状态观测器观测得到的AGV当前位姿进行比较得到AGV 全局位姿误差矢量通过MPC控制器进行优化和终端镇定控制,输出得到最优控制(t,X(t)),再根据式(4),结合参考速度Ur,即可得到 AGV最优速度控制信号U*;将U*=(v*,ω*)T输入系统对 AGV进行控制,最后在状态反馈时再通过一个状态观测器来提高AGV状态反馈精度,从而提高整个控制系统性能,实现系统全局渐进稳定。图3为AGV非线性模型预测控制框图。
2.1 MPC优化控制器设计
考虑由以下微分方程来描述的非线性系统:

此外,由于观测误差直接影响控制效果,为了能更加准确地估计AGV的当前位姿,本文为其设计了状态观测器。同时,针对有时候参考轨迹上会出现意外的障碍的情况,为了让整个控制功能更加完整,本文还考虑了避障功能模块。
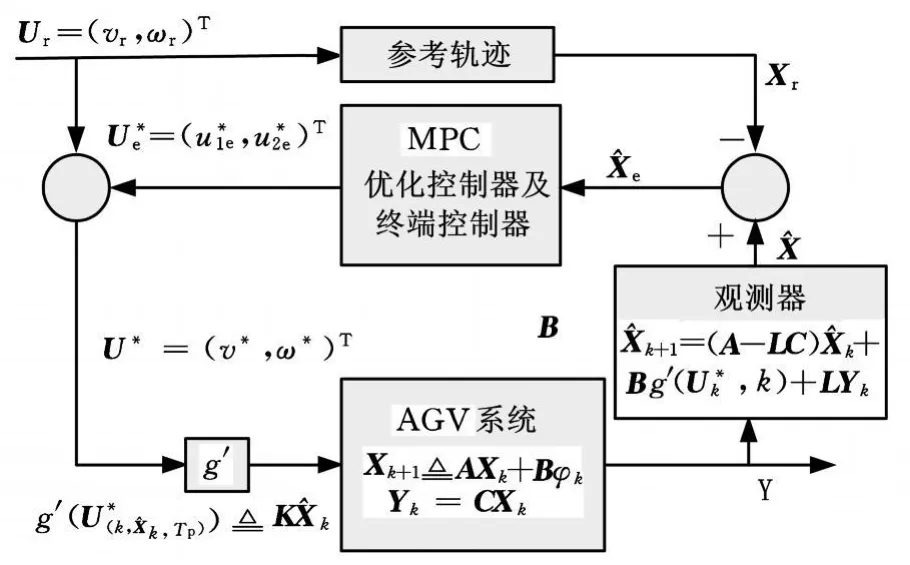
图3 控制框图
选取惩罚函数为预测状态及相应控制输入的二次函数:

2.2 MPC终端控制器设计

为了表示区别,我们用X eT=(x eT,y eT,θeT)T代表终端状态下的位姿误差,其中,xeT为终端状态下的x方向位置误差;yeT为终端状态下的y方向位置误差;θeT为终端状态下的θ姿态角误差。

综上,结合控制框图3,控制算法步骤可以概括如下:
(2)设δ为采样时间,在下一采样周期t+δ时刻,根据反馈得到的此刻的系统实际状态信息(t+δ)重新解决最优化问题(式(7)),获得此刻的最优控制输入(t,(t+δ)),则直接取该最优控制输入作为系统控制输入。如果此刻还在预测时域T p内(即t+δ≤τ≤t+T p),则直接取该最优控制输入作为系统控制输入;否则,如果此刻已经超过预测时域T p(即t+T p≤τ≤t+Tp+δ),则上面终端域设计的终端控制器启用,取上述终端控制器的作为系统控制输入。即输入系统的控制输入矢量应为
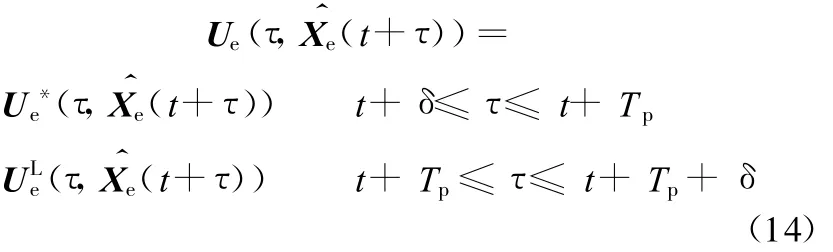
(3)重复上面的步骤直至达到满意的控制效果。
2.3 状态观测器设计
上述模型预测算法需要在每个采样时刻由状态观测器观测系统状态并据此更新优化问题的初始条件,从而滚动优化计算当前时刻的预测控制量。显而易见,优化问题的最优解是关于观测状态的函数,在这里我们引入一个优化控制器增益矩阵K的概念。

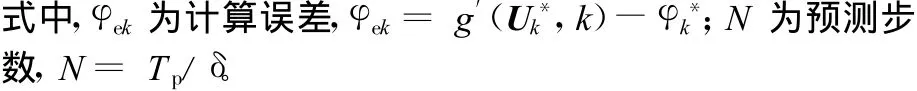
2.4 避障模块设计
假设AGV小车上部环绕安装有若干个红外传感器,它们能随时随地检测到前方的障碍物信息并反馈给小车控制器,以便能及时调整轨迹跟踪控制方案使之避过障碍物而不发生碰撞。对于移动障碍物,可以利用预测控制的方法来预测下一个T p的障碍物位姿信息以及障碍物移动速度,并通过计算类似上面的优化问题来获得系统的最优控制输入。设小车共环绕安装有Ns个红外传感器,第 j个的传感器测得的障碍物信息为[θob,j d ob,j](j=1,2,…,N),其中,θob,j为第j个
传感器与前方障碍物的夹角;dob,j为第j个传感器距离前方障碍物的直线距离。

3 仿真研究
为了验证本文所提出的控制算法的正确性和有效性,在MATLAB环境下编程,对AGV进行仿真计算和性能分析比较。
AGV期望轨迹取以(0,0)为圆心,以1为半径的圆,参考速度为v r=0.2m/s,ωr=0.2m/s。AGV小车实际初始值取x(0)=1.2m,y r(0)=1.2m,y r(0)=-0.3m,θ(0)=2π/3,v(0)=0.4m/s,ω(0)=0.3rad/s。
(1)在仅使用基本的模型预测跟踪控制率而不使用所设计的终端控制器的情况下,对AGV小车进行跟踪控制仿真,取基本模型预测控制器性能加权矩阵Q=diag(0.5,0.5,0.5),R=diag(0.1,0.1),预测时域与控制时域取为 Tp=T c=1s,采样周期取为δ=0.1s,即向前预测步数为N=10。跟踪效果如图4所示。
(2)结合所设计的预测模型终端控制器和状态观测器对AGV进行仿真试验,取模型预测控制器性能加权矩阵P=diag(1,1,1);性能系数取为α=2,β=1。预测时域T p、控制时域T c和采样周期δ参数设置同上。图5为AGV小车的跟踪效果图。
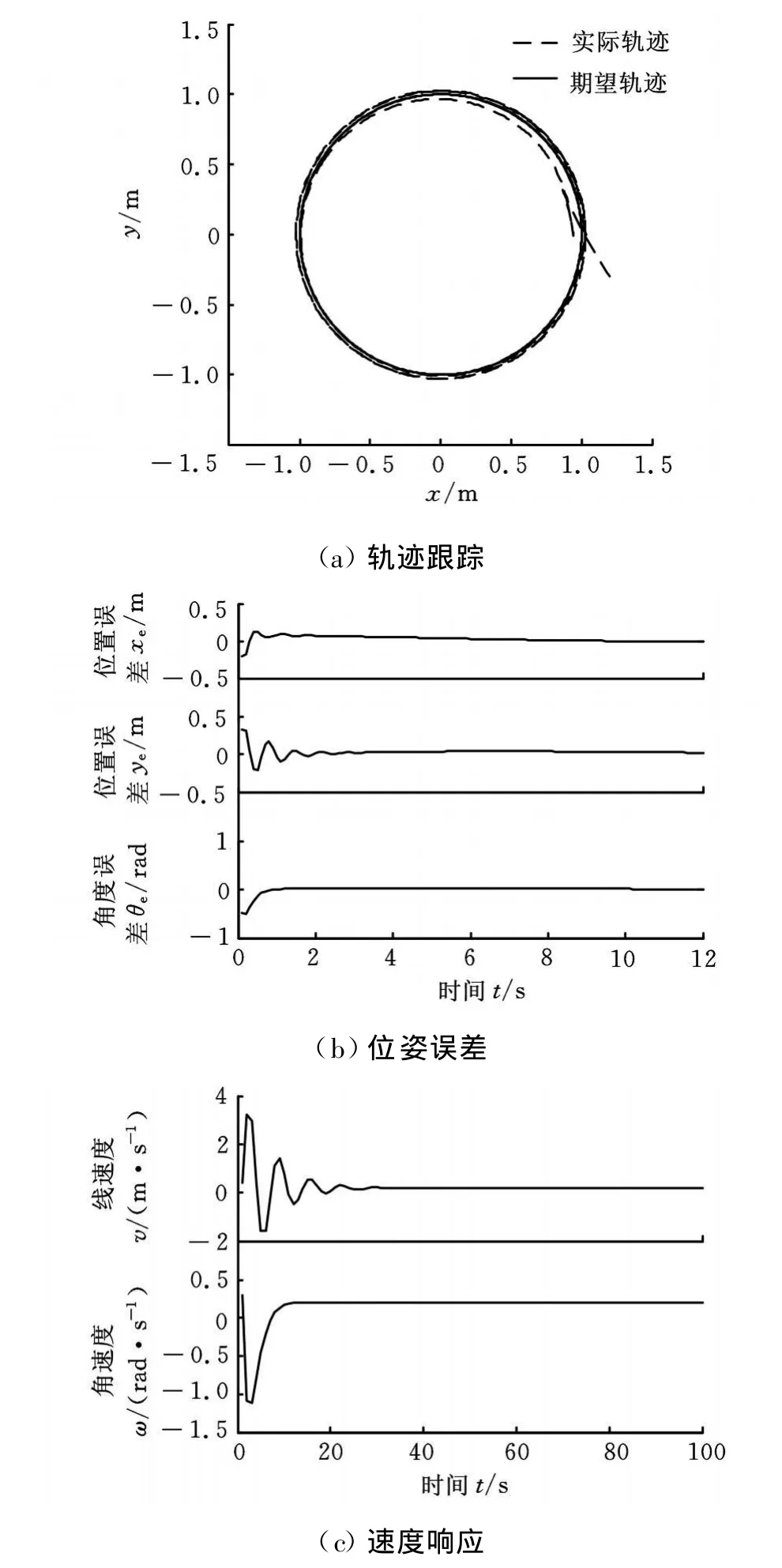
图4 不使用所设计的终端控制器的情况下的仿真结果
此外,为了验证所设计避障模块的有效性,对期望轨迹为简单的直线运动的AGV进行避障仿真试验。设期望轨迹上有四个障碍,避障控制器的系数取为kob=1.5,c1=0.1,c2=10,图6是小车躲避静态障碍物的效果图。
比较图4和图5仿真结果可见,由于本文所设计的控制律在设计时就考虑控制约束和终端镇定,而且在相应控制输入作用下,跟踪轨迹具有最优意义,同时状态观测器也进一步提高了反馈精度,因此在满足输入约束的前提下,系统能够在较短时间段内跟踪指定轨迹,取得良好的跟踪性能,表现为跟踪路径平滑、跟踪快、速度平稳。从图4可以看出,如果在设计控制器时不考虑实际存在的控制约束和终端镇定,闭环系统就很有可能会失去了稳定性保证,也就很难获得令人满意的跟踪效果。此外,图6避障仿真结果同时也验证了所设计的避障功能模块的有效性。
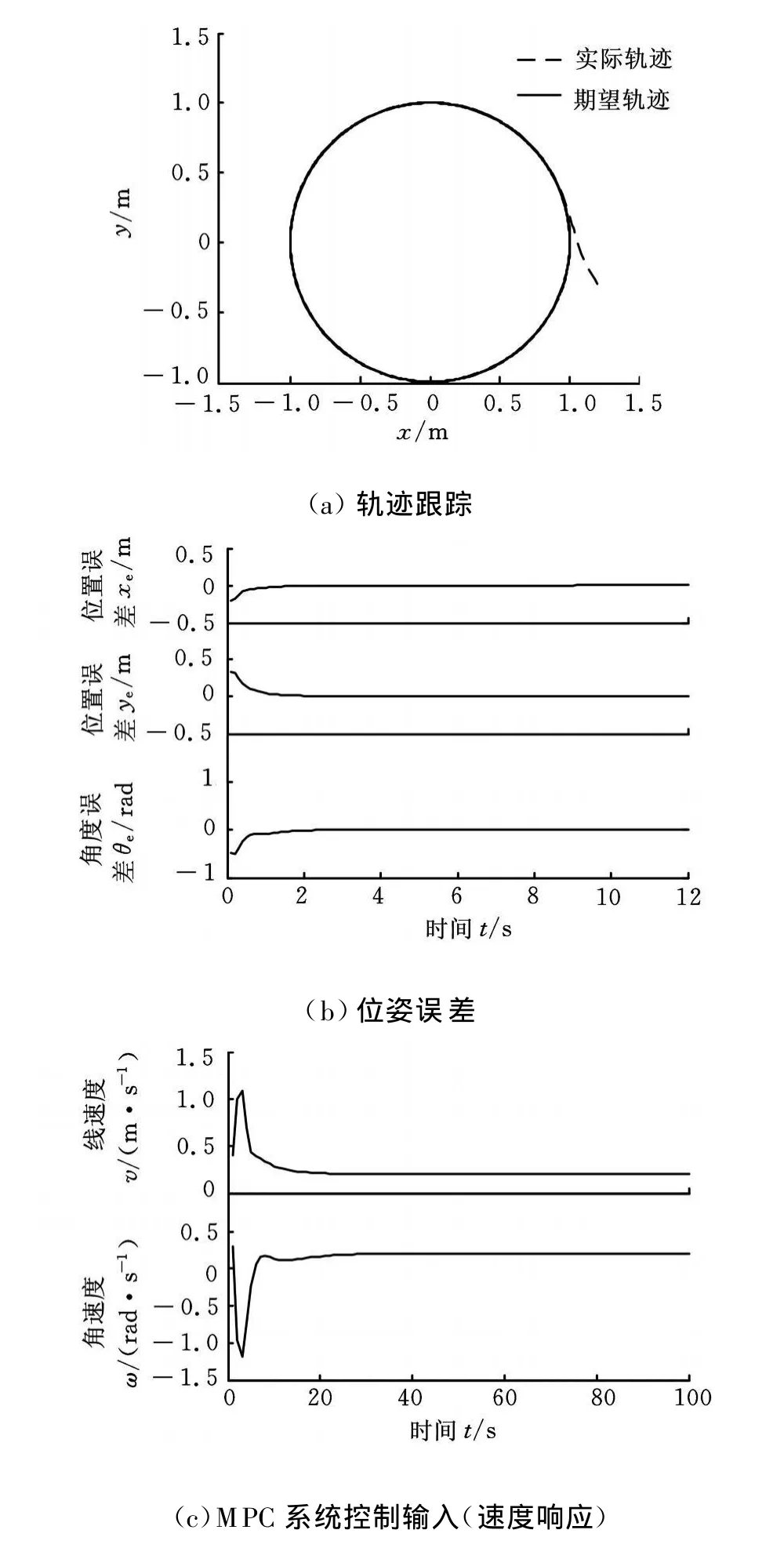
图5 使用所设计的终端控制器的情况下的仿真结果
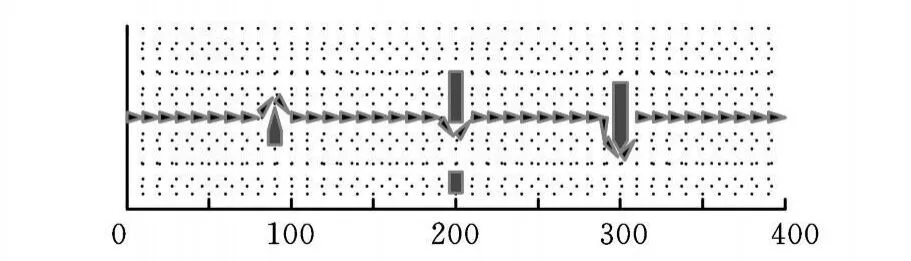
图6 AGV避障仿真结果
4 结论
以三轮AGV为研究对象,研究存在非完整约束和控制输入约束的AGV轨迹跟踪的非线性模型预测控制问题,设计了一种终端镇定控制器,并结合AGV的运动模型,使用状态观测器对含噪声的动态系统进行状态估计,进一步增强轨迹跟踪控制的效果,实现了系统全局渐进稳定。此外还考虑AGV的避障功能,设计了一种避障控制算法。计算机仿真结果证实了所设计轨迹跟踪算法的有效性和实时性。
[1] 闫茂德,吴青云,贺昱曜.非完整移动机器人的自适应滑模轨迹跟踪控制[J].系统仿真学报,2007,19(3):579-581.
[2] Dierks T,Jagannathan S.Control of Nonholonomic Mobile Robot Formations:Backstepping K inematics into Dynam ics[C]//16th IEEE International Conference on Control Applications,Part of IEEE Multi-conference on Systems and Control.Singapore,2007:94-99.
[3] Farzad P,Mattias PK.Adaptive Controlof Dynamic Mobile Robots with Nonholonom ic Constraints[J].Computers and Electrical Engineering,2002,28:241-253.
[4] Lin Sheng,Go ldenberg A A.Neural-netw ork Controlof Mobile Manipulators[J].IEEE Transactions on Neural Networks Manipulators,2001,12(5):1121-1133.
[5] Samson C.Controlof Chained Systems:App lication to Path Following and Time-varying Point-stabilization of Mobile Robots[J].IEEE Transactions on Automatic Contro l,1995,40:64-77.
[6] Fontes F A C C,Magni L.M in-max Model Predictive Controlof Nonlinear Systems Using Discontinuous Feedbacks[J].IEEE Transactions on Control System Techno logy,2003,48(10):1750-1755.
[7] Chen H,Allgow er F A.Quasi-infinite Horizon Non linear Modelp redictive Control Scheme with Guaranteed Stability[J].Automatica,1998,14(10):1205-1217.
[8] Mayne D,Raw ling J,Rao C,et al.Const Rained Model Predictive Control:Stability and Optimality[J].Automatica,2000,36:789-814.
[9] Timm F,Rolf F.Nonlinear Model Predictive Pathfollowing Control[J].Lecture Notes in Control and In formation Sciences,2009,384:335-343.
Non linear Model Predictive Control of Trajectory Tracking for Nonholonomic AGV
Zhao Han Yin Xiaohong Wu Yanming
Hefei University of Techno logy,H efei,230009
Considering the kinem atic model o f three-wheeled AGV w ith non-holonomic constraint and input saturation,a nonlinearm odel predictive controlwas studied and an united control algorithm of tracking and stability was proposed.Firstly,an optimal controllerwas obtained based on the princip les of model predictive control.Second ly,a terminal controller and an invariantterm inal region were designed in order to keep the AGV system stable.Then,the noise problem of state estim ation w as solved by using a state observer,which im proves the localization precision and enhances the control effectiveness.Finally,a module was designed to avoid obstacle.The designed control algorithm has generality for kinematic model of other wheeled mobile robots.Computer simulation results show its correctness and validness.
automatic guided vehicle(AGV);model predictive control;stability;observer;trajectory tracking
TP24
1004—132X(2011)06—0681—06
2010—05—24
国家“十一五”支撑计划资助项目(2006036003131);国家高技术研究发展计划(863计划)资助项目(2006AA 11A 109)
(编辑 苏卫国)
赵 韩,男,1957年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为数字化设计与制造、汽车、智能车、磁力机械等。发表论文300余篇。尹晓红,女,1985年生。合肥工业大学机械与汽车工程学院博士研究生。吴焱明,男,1968年生。合肥工业大学机械与汽车工程学院副教授。

