对数曲面楔块的PCE型离合器动力学特性分析
吴 凯 严宏志 何明生 谭援强
1.中南大学,长沙,410083 2.湘潭大学,湘潭,411105
对数曲面楔块的PCE型离合器动力学特性分析
吴 凯1严宏志1何明生1谭援强2
1.中南大学,长沙,410083 2.湘潭大学,湘潭,411105
在分析强制连续约束型离合器(PCE型离合器)结构和工作原理的基础上,对离合器关键零件——楔块进行了设计,并构造出了对数曲面楔块与单圆弧曲面楔块PCE型离合器的三维模型。将模型导入ADAMS中进行动力学仿真,模拟了离合器楔合过程的动作过程。对两种离合器的楔合时间、接触力及溜滑角等参数的分析表明,对数曲面楔块的离合器楔合迅速,其瞬态冲击力与稳态接触力小于单圆弧曲面楔块离合器的瞬态冲击力与稳态接触力。
对数曲面楔块;PCE型离合器;接触力;动力学
0 引言
强制连续约束型离合器(PCE型离合器)应用于矿山机械、造纸机械、食品机械、起重运输机械以及发电设备等领域。楔块型面设计是PCE型离合器结构设计中的关键,直接影响离合器的工作性能及寿命。
在楔块型面设计与动力学分析方面,国内外已进行了研究:胡大国[1-2]研究了对数螺线超越离合器工作楔角及承载能力的计算方法;何为[3]针对对数螺线楔合面的设计技术进行了研究;Chesney等[4]给出了斜撑式离合器设计的相关方程式,并讨论了其静态和动态特性;Peeken等[5]分析指出离合器急速地楔合的动作可能导致楔块突然跑出;W illiams等[6]分析了斜撑式离合器的动态特性,建立了离合器在楔合过程中多因素的滑动模型;Chassapis等[7]建立了斜撑式离合器在楔入过程及楔合状态下的非线性刚度的动力学分析模型;Vernay等[8]通过实验分析得出了导致离合器破坏的多种原因;Xu等[9-10]分析了离合器装配情况下楔合的动力学特性。
上述研究没有建立斜撑式超越离合器的动力学模型,对斜撑式超越离合器在楔入过程中所表现的力学特性也没有进行相关的研究。本文设计出一种对数曲面楔块PCE型离合器,通过动力学仿真,研究了其楔合时间、接触力等参数的变化规律,并与传统的单圆弧型楔块PCE型离合器进行性能对比,为设计出长寿命、楔合特性好的PCE型离合器提供新的思路。
1 PCE型离合器的结构和工作原理
目前,普遍采用的斜撑式超越离合器有两种类型,即全相位型(full-phasing)和强制连续约束型(PCE型)。PCE型离合器(图1)楔块为一成组摩擦元件,PCE型离合器依靠楔块在内外环之间的楔住作用来传递扭矩,其基本结构如图1a所示。
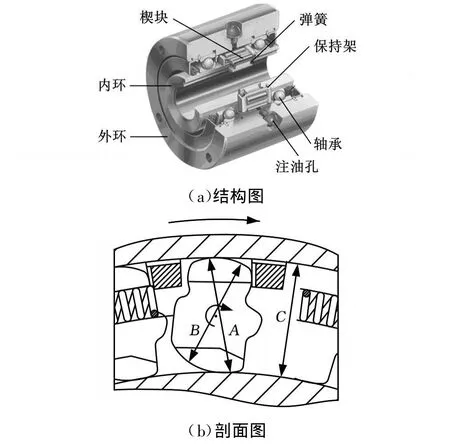
图1 PCE型离合器
外环(主动件)按顺时针方向的转速大于内环(从动元件)转速时,因弹簧的张紧力和楔块与环面的摩擦力,使得楔块围绕其自身的中心按顺时针方向转动,由于楔块的尺寸A(图1b)大于两环之间的径向距离C,于是楔块便楔入内外环之间,从而使两环相互闭锁,离合器处于传动状态。内环按顺时针方向转速大于外环转速时,楔块和环之间的摩擦力使得楔块围绕其自身的中心按逆时针方向转动,因楔块尺寸B小于两环之间的距离C,楔块脱离楔住状态,内外环彼此独立运动,离合器处于超越状态。
PCE型离合器一般采用单一保持架和弹簧,这种离合器的楔块在其侧面具有特殊的几何形状的凸缘。凸缘在过载条件下使楔块相互邻接,因此形成一个不能“翻转”的“整体”结构。
2 对数曲面楔块及单圆弧曲面楔块设计
楔块结构及相关几何参数如图2所示。图2中,P、Q两点分别为楔块与内外环的相切点。QE与PQ的夹角为内楔角ν,OP与OE的夹角为ψ,OP与PQ的夹角为ω,AC为Q点切线,BD为O′Q的垂线,AC与BD的夹角为α,O′Q为阿基米德螺线的极径ρ,O′Q 与O O′的夹角为β,O′Q 与PQ的夹角为γ,PQ长为l,r o为楔块上圆弧半径,R o为离合器外套内环半径,Ri为离合器内套外环半径。
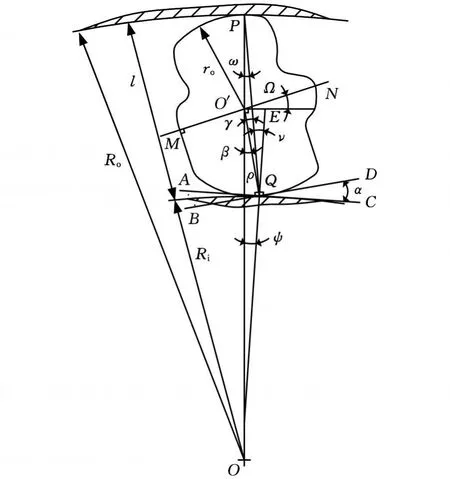
图2 楔块的几何模型
2.1 对数曲面楔块的设计
对数螺线的极坐标方程为

式中,a、m为常数;ρ为极径;θ为极角。
如图3所示,由微分几何知识知,曲线在点P的切线BE与向量半径的垂直线FC的夹角λ′可由下式求得:
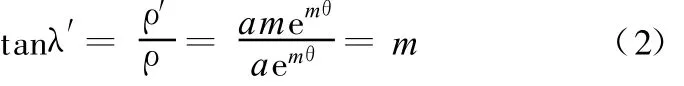
楔块按照J=9.5mm(J为内环外径与外环内径之差,如图2所示)的规格进行设计,根据对数曲面楔块的几何关系(图3),可得以下各关系式:
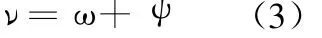
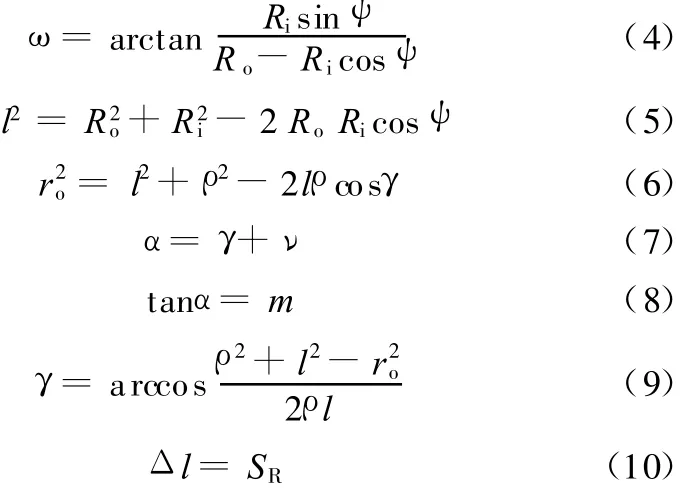
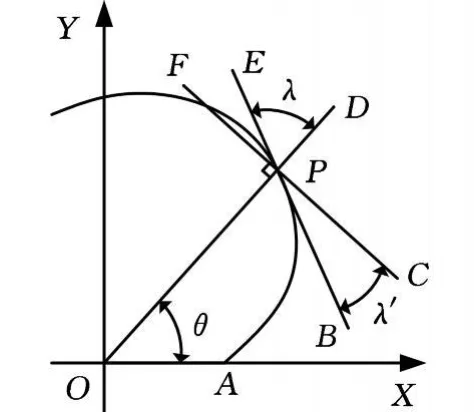
图3 对数螺线
式中,SR为楔块凸轮升程。
为了求解出以上方程组,需给定如下初始设计参数。
2.1.1 起始楔角
PCE型离合器是依靠摩擦角即楔角来转递转矩的,楔角即径向线和作用力线之间的夹角。在图2中,ν为楔块在内环滚道上的楔角,ψ为楔块在外环滚道上的楔角,根据几何关系可表示为
ν=ω+ψ (11)
PCE型离合器在正向行程中要求锁紧,而这种锁紧的特点是:①不依赖外加压力造成摩擦阻力来形成锁紧状态;②该锁紧状态在承受很大载荷时(在构件不被破坏的条件下)仍不打滑。这个条件只有力学中的“自锁”状态才能满足。PCE型离合器的“自锁条件”是楔块摩擦角的正切值小于摩擦因数,即

另外,PCE型离合器在反向实现“超越”时,要求自动“解锁”,而不需要另外通过其他措施来解锁。这种反向解锁超越也只有力学中的自锁状态才能满足,在满足上述条件的情况下,取起始楔角ν0=2°30′[11]。
2.1.2 有效凸轮升程
有效凸轮升程为楔块从楔入到楔合过程中楔块转动的凸轮升程,它必须大于离合器总的径向变形量Δtotal,否则,将发生“离合器翻转”即楔块翻转,导致扭矩传递失效。一般情况下,总的径向变形量为楔块有效升程的50%,这里取有效凸轮升程S R=0.381mm[11]。
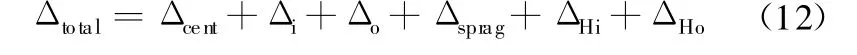
式中,Δcent为外环由离心力引起的径向变形;Δo为外环的径向变形;Δi为内环的径向变形;Δsprag为斜撑滚子的压缩变形;ΔHo为斜撑滚子与外环接触处的赫兹变形;ΔHi为斜撑滚子与内环接触处的赫兹变形。
通过给定合理的起始楔合状态时的极角θ0(π <θ<2π),求解式(1)、式(3)~ 式(10)构成的方程组,得出楔块上圆弧半径r0=4.9233mm以及对数曲线方程:
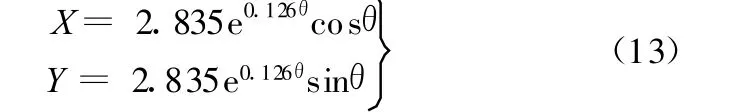
2.2 单圆弧曲面楔块设计
为了与对数曲面楔块的动力学特性进行比较,在此也设计了单圆弧楔块结构,并建立单圆弧楔块离合器动力学模型。
如图4所示,楔块以上圆弧圆心为原点坐标,其半径为r0=5.1695mm;下圆弧为一偏心圆弧段,其偏心坐标为(0.6143,0.3194)mm,半径为5.2765mm,在此基础上构造其三维模型。
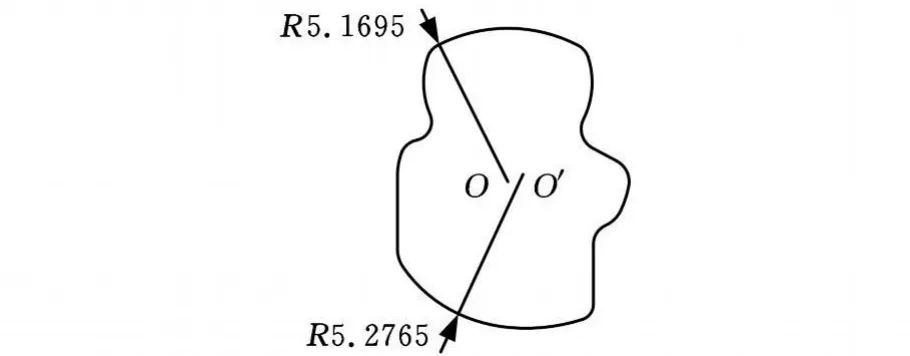
图4 单圆弧曲面楔块
3 离合器动力学模型的建立
采用ADAMS软件对离合器进行动力学仿真分析。为便于研究,对超越离合器的刚体模型做如下假设:①装配间隙为零,制造误差忽略不计;②转动约束为理想约束;③各部件均视为刚体;④暂不考虑楔块和滚道变形对动力学性能的影响。
3.1 施加约束和载荷
约束的实现是建立虚拟样机的重要内容,是仿真分析真实可靠性的保证。约束定义的是机构内两构件的连接关系,它限制两构件在某个方向上的相对运动。根据超越离合器的运动规律,本系统加入的约束和载荷如下:①超越离合器的内环、外环、保持架相对于地面加旋转副约束;②楔块和滚道之间施加实体-实体碰撞力,以仿真楔块和滚道的接触碰撞;③各个楔块与保持架之间也施加接触力;④超越离合器的外环施加一个恒负载转矩,模拟超越离合器工作时的负载;⑤在超越离合器的内环施加恒转速运动;⑥在各个斜撑式超越离合器的每一个楔块上施加恒力矩,以模拟离合器工作时弹簧提供给每个楔块进入楔合时所需的力。
整个超越离合器系统包括36个构件、3个旋转副、1个驱动、132个接触。
3.2 仿真参数设置
(1)碰撞参数。离合器楔块碰撞激励力可以看作是两个变曲率半径柱体撞击问题,根据ADAMS中对碰撞力的定义与Hertz静力弹性接触理论计算出碰撞参数。
楔块与内环接触圆弧的接触刚度的值是9 807 230N/m。根据经验数据,取阻尼系数值为9807N◦s/m,最大阻尼时的击穿深度取0.1mm,非线性指数取1.5。
楔块与外环接触圆弧的接触刚度的值是11 009 229N/mm。根据经验数据,取阻尼系数值为11 009N◦s/mm,最大阻尼时的击穿深度取0.1mm,非线性指数取1.5。
(2)摩擦参数。在ADAMS中,接触定义包括4个摩擦参数:静摩擦因数、动摩擦因数、滑动速度、过渡速度,它们根据离合器的材料与运动特性分别被设定为 0.08 、0.05 、0.1m/s、0.2m/s。
(3)工况参数。给离合器内环施加一个恒转速7200°/s,外环施加1326.25N◦m的力矩。
3.3 仿真模型建立
由于楔块曲面构造的复杂性以及离合器的装配要求,并且为了便于仿真分析,采用三维构造软件UG进行建模,所构造的模型如图5a所示。将UG中建立的三维模型导入ADAMS,得到加约束的ADAMS虚拟样机模型如图5b所示。
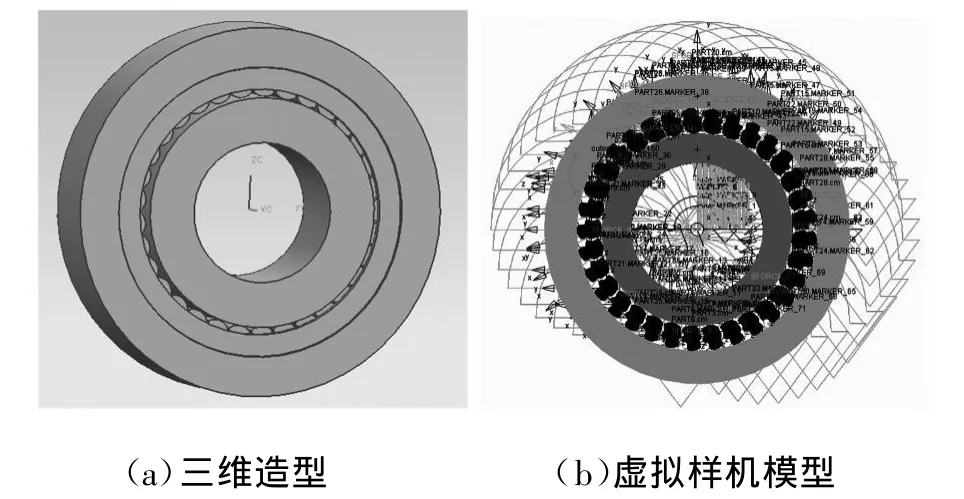
图5 离合器模型
4 仿真结果及分析
利用ADAMS软件并按照前述模型参数及约束的设定,可以分析得到离合器楔块与内外环的接触力、楔合时间及溜滑角等参数随时间变化的规律。
4.1 楔块与内外环的接触力
图6所示为两种离合器不同楔块(均为33个)中冲击接触力最大的楔块的接触力随时间的变化规律,可以看出,离合器在刚启动时存在冲击。其中,对数曲面楔块与内外环之间的最大冲击接触力为178.4kN,单圆弧曲面楔块与内外环之间的最大冲击接触力为652.8kN,后者是前者的3.7倍,这是造成楔块低周疲劳失效的主要原因[11]。
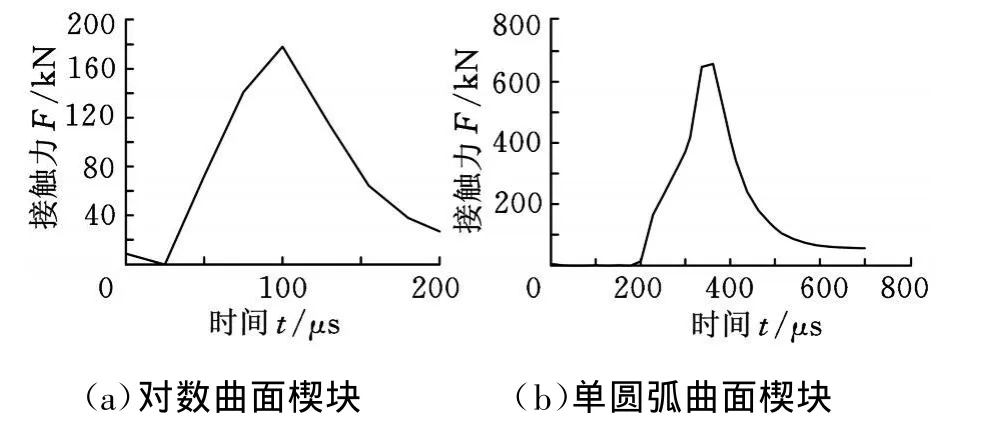
图6 楔块与内外环最大接触力随时间的变化曲线
通过对ADAMS仿真结果进行后处理得到楔块与内外环平均接触力随时间的变化规律如图7所示,可以看出,对数曲面楔块与内外环之间的平均接触力为7.45kN,单圆弧曲面楔块与内外环之间的平均接触力为20.329kN,后者是前者的2.7倍。
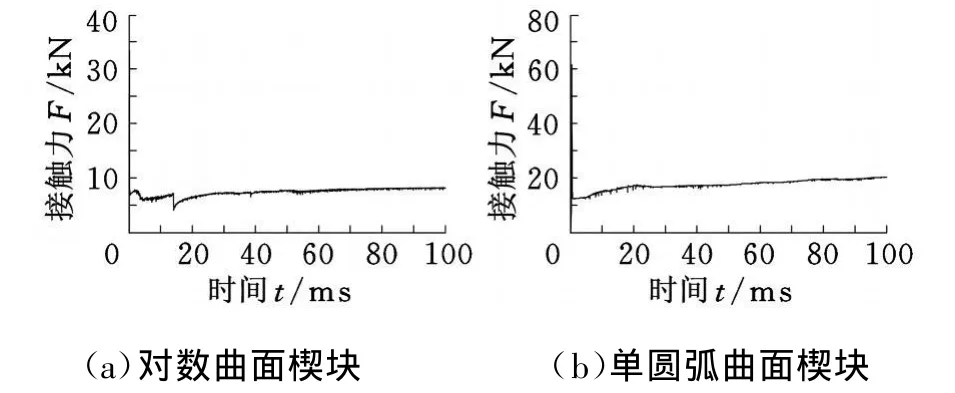
图7 楔块与内外环平均接触力随时间的变化曲线
4.2 离合器楔合时间
离合器的楔合时间即为离合器从超越状态到内环与外环同步运行时的时间。楔合时间的长短反映了离合器工作的灵敏性,是一项重要指标。本文分析的是内环输入转速、外环带负载的形式,因此,分析外环角速度的变化可得出楔合时间。图8a为对数曲面楔块PCE型离合器外环角速度随时间的变化图,可以得出其楔合时间为2ms。由图8b可知,单圆弧曲面楔块PCE型离合器的楔合时间约为13ms。
4.3 离合器溜滑角
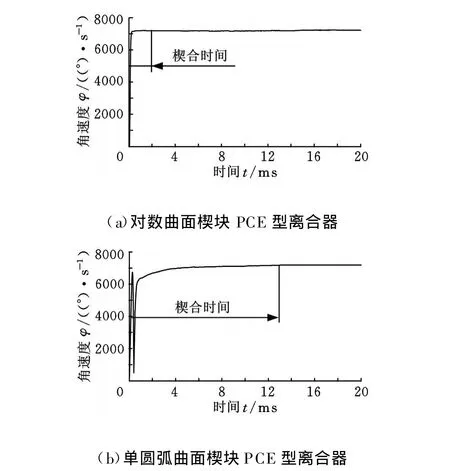
图8 外环角速度随时间的变化曲线
溜滑角是离合器内外环运动相对转角,它是反映离合器工作灵敏度的又一项指标。离合器溜滑角随时间的变化曲线如图9所示。由图9a可知,对数曲面楔块离合器在13ms时溜滑角存在一个峰值1.13°,之后下降,在 100m s时溜滑角为 0.29°。由于离合器是由内环带动外环转动的,从溜滑角变化趋势可以看出内环转速在峰值出现之前高于外环转速,之后则外环转速超越了内环,因而其相对转角变小。由图9b可知,单圆弧曲面楔块PCE型离合器的溜滑角在25m s之前相对转动较大,之后缓慢增大,在100ms时刻达到9.53°。
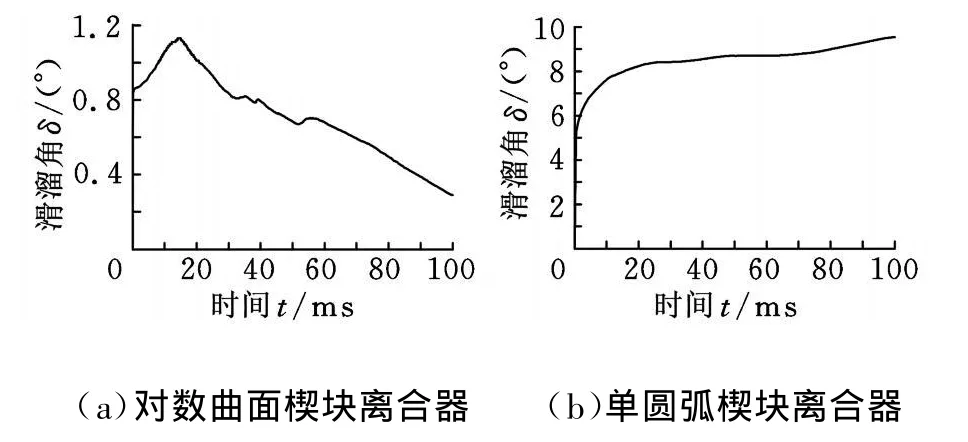
图9 离合器溜滑角随时间的变化曲线
综合以上分析可以得到单圆弧楔块离合器与对数曲面楔块离合器的特性参数,如表1所示。
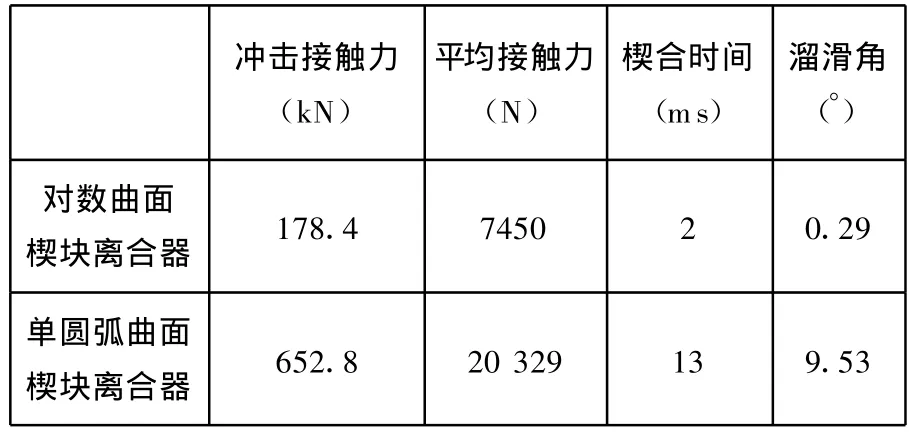
表1 离合器参数
5 结论
(1)所设计的对数曲面楔块离合器的楔合时间短、溜滑角小,具有较好的响应特性,有利于减小楔块的磨损。
(2)对数曲面楔块离合器在楔合之后接触力平稳且其楔块与内外环的最大冲击接触力远小于单圆弧曲面楔块与内外环的最大冲击接触力,这将非常有利于提高楔块的疲劳寿命。
[1] 胡大国.对数螺线超越离合器的楔角计算[J].火炮发射与控制学报,1996(1):20-30.
[2] 胡大国.对数螺线超越离合器的承载能力计算[J].火炮发射与控制学报,1996(4):32-37.
[3] 何为.超越离合器内星轮对数螺旋楔合面的设计[J].苏州大学学报(工科版),2002,22(5):38-42.
[4] Chesney D R,K remer JM.Generalized Equations for Sp rag One-w ay Clutch Analysis and Design[C]//Proceedings of the 1998 SAE International Congress&Exposition.Detroit,1998:173-184.
[5] Peeken H J,Gold P W.Coup ling and Clutches—state of the A rt[C]//1996 Proceedings of the International Conference on Gears.Dusseldorf,Germany,1996:47-60.
[6] Williams F C,Tipping D,Henry T A.An Imp roved Sp rag Clutch[C]//4th Word Congress on the Theory of Machines and Mechanics.Tyne,England:University o f New castle,1975:593-598.
[7] Chassapis C,Lowen G G.High Speed Dynam ics of a Press Fed Mechanism[C]//21st ASME Biennal Mechanism s Con ference.Chicago,1990:415-427.
[8] Vernay P,Ferraris G.Transient Behavior of a Sp rag-type Over-running Clutch:an Experimental Study[J].Journal of Sound and V ibration,2001,248(3):567-572.
[9] Xu T,Low en G G.A New Dam ping Model for Non-linear Stiffness System s with Variable Preload Disp lacements and Constant Amplitude Decay Ratios[C]//22nd ASME Biennal Mechanisms Conference.Scottsdale,1992:27-33.
[10] Xu T,Lowen G G.Closed Solution for the Elasticdynamic Behavior of an Industrial Press Feed Mechanism[C]//1994 ASME Design Technical Conferences,Part 2.M inneapolis,1994:41-51.
[11] 朱自冰.高速超越斜撑离合器设计技术研究[D].南京:南京航空航天大学,2004.
Dynam ics Analysis of Logarithm Curved Sur face Sprag PCE Clutch
Wu Kai1Yan Hongzhi1He M ingsheng1Tan Yuanqiang2
1.Central South University,Changsha,410083 2.Xiangtan University,Xiangtan,H unan,411105
On the basis of analysis of a clutch structure and work princip les,the sprag,key element of the clutch,was designed.Meanw hile,three-dimensionalmodelsof the logarithm curved surface sprag PCE clutch and the single arc curved surface sprag PCE clutch were formed.Im porting the model into ADAM S,the engagement p rocess o f the clutchwas simu lated.Through the analysis of the engagement time,contact forces and sliding ang le,it indicates that the logarithm curved surface sp rag clutch engages rapid ly and both transient impact and steady contact force are lower than that of the single arc curved surface sprag clutch.
logarithm curved surface sprag;positive-continuous-engagement clutch(PCE clutch);contact force;dynam ics
TH 13
1004—132X(2011)06—0647—05
2010—03—04
复杂轨迹加工工艺及装备教育部工程研究中心开放课题
(编辑 苏卫国)
吴 凯,男,1983年生。中南大学机电工程学院硕士研究生。主要研究方向为机械设计及理论。严宏志,男,1964年生。中南大学机电工程学院研究员、博士研究生导师。何明生,男,1986年生。中南大学机电工程学院硕士研究生。谭援强,男,1966年生。湘潭大学机械工程学院教授、博士研究生导师。

