预测高速混合球轴承的滑动与自旋摩擦功率

喻 炜 任成祖 刘胜超 王东峰

1.天津大学先进陶瓷与加工技术教育部重点实验室,天津,300072 2.洛阳轴研科技股份有限公司,洛阳,471039

预测高速混合球轴承的滑动与自旋摩擦功率

喻 炜1任成祖1刘胜超2王东峰2

1.天津大学先进陶瓷与加工技术教育部重点实验室,天津,300072 2.洛阳轴研科技股份有限公司,洛阳,471039

高速工况下,轴承摩擦发热量剧增,因此预测球在内外圈滚道的滑动和自旋摩擦功率对高速球轴承的选用、分析和优化意义重大。用刚柔混合动力学有限元法仿真高速混合球轴承,结果显示,轴向载荷从16kN到24kN、内圈转速在较大范围内变化时,球在内外圈的旋滚比(球自旋角速度与滚动角速度之比)、自旋摩擦功率分别大致相等,分析高速混合球轴承滑动与自旋摩擦功率时不宜忽略球在外圈的旋滚比。适当增加轴向预载可以显著减小内圈旋滚比。

高速混合球轴承;滑动;自旋摩擦功率;有限元法

0 引言

高速工况下,轴承球离心载荷剧增(通常大于外载荷),摩擦发热量增大,这些都恶化了轴承运行环境。预测球在内外圈滚道的滑动与自旋摩擦功率对于高速球轴承的选用、分析与优化都具有非常重要的现实意义。Jones[1]的经典拟静力学理论为了简化计算,假设在低速和高速工况下轴承球分别在内圈和外圈滚道无自旋地滚动(即内圈和外圈控制,套圈控制假说),该理论在一定条件下(低速和高速)是实用的和近似的。Harris[2]考虑弹性流体动力润滑的作用,进一步发展了球轴承的拟静力学理论;Boness等[3-4]应用经验方程简化计算油膜切向力,获得了与试验较一致的结果;A ltintas等[5]和Chen等[6]简化了拟静力学模型;A lfares等[7]和A ntoine等[8]将描述接触角和接触变形关系的平衡方程减少为两个;Jedrzejew ski等[9]采用该简化拟静力学模型分析了电主轴轴承轴向位移;Liao等[10-11]提出简化的拟静力学模型并进一步引入热效应。拟静力学理论需要迭代求解一组非线性方程组,方程繁多、选初值困难、迭代不易收敛且未能考虑套圈、轴和轴承室变形的影响。

动力学方面,Walters[12]建立了在六自由度系统中考虑球-滚道滑动和保持架动力学的球轴承动力学解析模型,后来Gupta[13-14]改进了该模型,并开发出 ADORE程序。Meeks等[15-17]将Walters和Gupta模型所用固定的惯性坐标系改为旋转坐标系,用矢量表示方式写出运动方程组,从而使相应的程序(BABERDYN)更精确更有效率。SKF公司开发了六自由度动态分析模型[18],但该模型并未公开。Ghaisas等[19]和Weinzapfel等[20]用离散单元模型并考虑柔性保持架,分析了保持架的稳定性。A shtekar等[21]进一步将表面缺陷引入离散单元模型。然而,动力学分析模型需要对每一时刻每个球与内外圈赫兹接触应力、每次保持架与球或内外圈之间的碰撞、球与内外圈接触处摩擦力进行积分,这都需要大量计算。另外,动力学理论也未能考虑套圈、轴和轴承室变形的影响。

本文的主要目标是采用刚柔混合动力学有限元法(finite elementmethod,FEM)对高速混合球轴承(hybrid ball bearing,HBB)进行仿真。在高速工况下,外圈控制假说成立,拟静力学理论[1,22]适用,故用拟静力学理论计算球在内外圈滚道的旋滚比(球自旋角速度与滚动角速度之比)、球公转角速度和球自转角速度俯仰角等以验证仿真结果。然后分析自旋摩擦功率随轴向载荷和转速变化的规律。用刚柔混合动力学FEM能方便地仿真复杂工况下的球轴承、新型球轴承以及轴-轴承系统的动力学。

1 刚柔混合有限元模型

使用非线性有限元分析软件ABAQUS对HBB进行刚柔混合显式动力学分析,所用轴承的几何尺寸参数和材料参数分别见表1和表2。

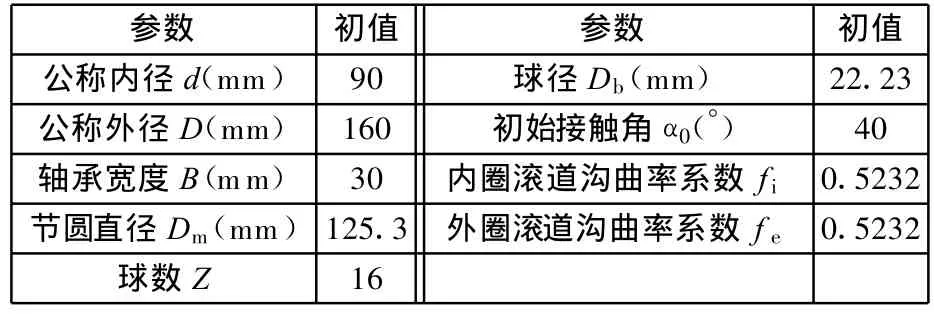
表1 轴承几何尺寸参数

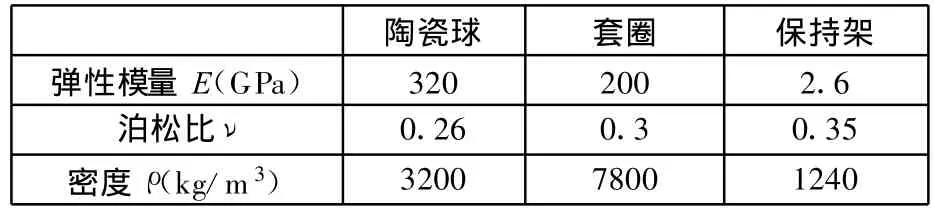
表2 材料参数

建立HBB有限元模型时,为方便分析而采取必要的简化。

(1)为方便数据处理及与理论结果比较,只施加轴向载荷。

(2)陶瓷球的弹性模量是钢套圈弹性模量的1.6倍,因此将陶瓷球简化为解析刚体以减小计算量,在球心位置处定义点质量单元,将球的质量和转动惯量定义于该点质量单元。该简化对球与套圈的接触应力、接触变形影响有限,对球与套圈的接触力、接触角以及球的运动影响很小。本文主要是为了获取接触角、接触载荷以及球运动等参数的值,接触应力和接触变形可以用接触载荷和接触角等参数通过静态分析方法获得精确值。

(3)保持架由于几何形状复杂,难以定义为解析刚体,本文将之定义为离散刚体以减小计算量。

(4)球与套圈、球与保持架之间的摩擦定义为库仑摩擦,摩擦因数μ取两个固定值 0.05和0.11以分别仿真两种不同的润滑状态。

边界条件:外圈底平面固定,内圈和保持架只保留轴向转动与轴向移动两个自由度。接触条件:定义球与内外圈、球与保持架接触,接触属性中的库伦摩擦因数μ分别定义为0.05和0.11。网格和单元:由于球与套圈接触区域狭长,故需要对内外圈进行局部网格细化,所选单元为增强沙漏控制、二次精度的8节点三维实体减缩积分单元(C3D8R),划分了网格的模型见图1,内外圈的单元数共为430 000个。分析步:为考虑轴承的离心效果,选取显式动态分析步,第一步加载轴向载荷,第二步用角加速度的方式加载内圈转速至设定值,第三步内圈匀速转动。

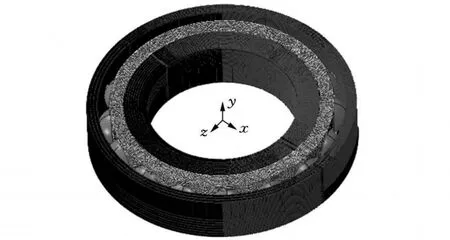
图1 混合陶瓷球轴承有限元模型

2 有限元结果与分析

分别取轴向载荷F a为16kN和24kN,内圈转速n i为10 000 、16 000、20 000、25 000r/m in,摩擦因数μ为0.05和0.11进行分析。稳定运转阶段的球轴承球与内外圈的接触载荷、球角速度等参数是平稳波动的,分别取平均值,并做相应处理,所得结果如图2～图7所示。

2.1 有限元结果验证

图2、图3分别示出了不同轴向载荷下,球在套圈滚道的旋滚比s随内圈转速和摩擦因数的变化曲线。旋滚比的有限元分析(FEA)值的变化趋势与Harris拟静力学理论值一致。随着转速增加,球-内圈旋滚比单调递增,而球-外圈旋滚比单调递减。转速越高且轴向载荷越低,则球-内圈旋滚比的FEA结果越接近于Harris理论值,球-外圈旋滚比的FEA值越接近于零。当轴向载荷为16kN且内圈转速为25 000r/min时,球-内圈旋滚比的FEA值和Harris理论值吻合。这与套圈控制假说的高速工况下,球-外圈旋滚比为零一致,从而验证了有限元结果的准确性。

当轴向载荷为 16kN 且转速小于12 000r/m in时,球-内圈旋滚比小于球-外圈旋滚比,套圈控制假说并不适用这些工况。当轴向载荷为16kN且转速大于12 000r/m in时,球-内圈旋滚比大于球-外圈旋滚比。轴向载荷为24kN时的规律与16kN时的类似。改变摩擦因数对球与内外圈旋滚比的FEA值影响不大。

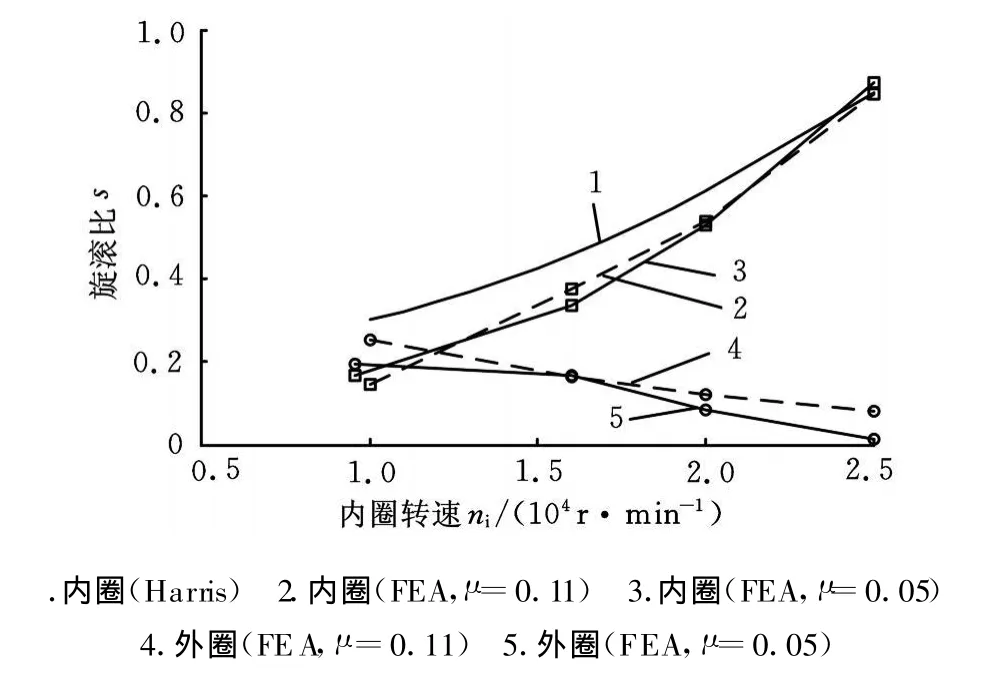
图2 旋滚比随内圈转速变化(F a=16kN)

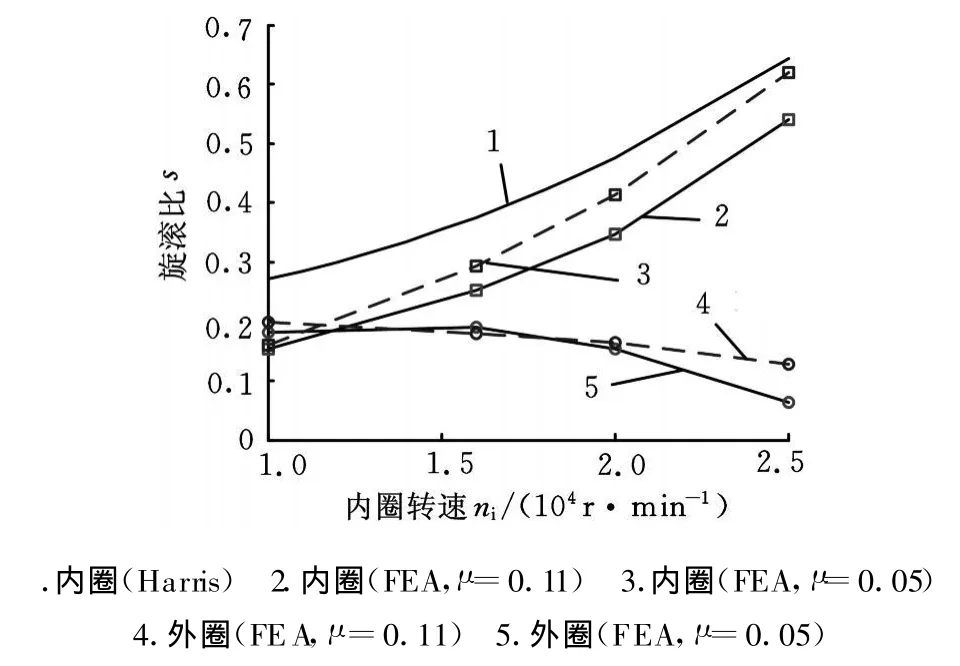
图3 旋滚比随内圈转速变化(F a=24kN)

比较图2和图3可知,随着轴向载荷的增大,内圈旋滚比显著减小,外圈旋滚比增大但增大程度相对内圈很小。这说明对于高速HBB,适当地增大轴向预载可以显著减小内圈旋滚比而使外圈旋滚比增大不多。需要注意的是,增大轴向预载会缩短轴承疲劳寿命、增大轴承自旋摩擦功率(即摩擦生热,参见2.3节)和增加磨损。

2.2 球公转角速度和球自转角速度俯仰角

图4示出了球公转角速度n m(即保持架转速)与内圈转速之比 nm/ni的 FEA值与 Harris理论值的比较情况,可见两者吻合较好。n m/n i随内圈转速n i的单调递增而单调递增、随轴向载荷F a的增大而减小。摩擦因数μ对球公转角速度的FEA值影响不大。

图5示出了球自转角速度俯仰角β的FEA仿真值和Harris理论值的比较情况,可看出两者均随着内圈转速的单调递增而单调递减、随着轴向载荷的增大而增大。当内圈转速为10 000r/min时,俯仰角β的仿真值大于Harris理论值,随着转速的增加,俯仰角的仿真值趋近于Harris理论值。滑动摩擦因数 μ对俯仰角的FEA值影响不大。

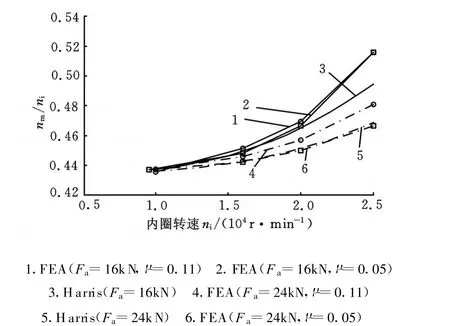
图4 n m/n i随内圈转速变化

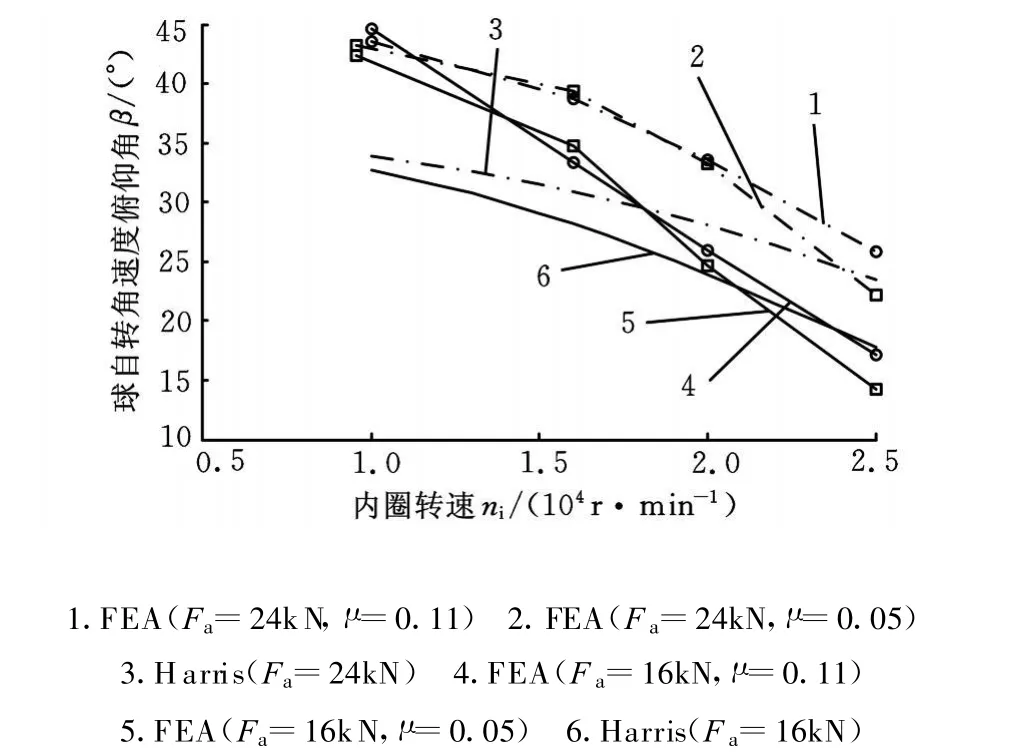
图5 球自转角速度俯仰角随内圈转速变化

上述结果再次证明了本文所建有限元模型的有效性。下面分析自旋摩擦功率随轴向载荷和内圈转速的变化规律。

2.3 混合球轴承的自旋摩擦功率

如图6所示,随着内圈转速的单调递增,轴承自旋摩擦功率P S单调递增;随着轴向载荷增大,轴承自旋摩擦功率增大。前述适当增加轴向预载能使内圈旋滚比显著减小而使外圈旋滚比增加不大,但值得注意的是,增大轴向预载使得整个轴承的自旋摩擦功率增大。H arris理论对自旋摩擦功率的估计偏低,因为理论认为球在外圈的自旋摩擦功率等于零。

如图7所示,单个球在内外圈的自旋摩擦功率随内圈转速和轴向载荷的变化规律与球在内外圈的旋滚比变化规律类似。不同的是,随着轴向力增大,球在内圈的旋滚比减小、在外圈的旋滚比略增,而球在内外圈的自旋摩擦功率都增大。转速在10 000～15 000r/min时,球在内外圈的自旋摩擦功率大致相等,分析轴承自旋摩擦功率时不宜忽略球在外圈的自旋摩擦功率。

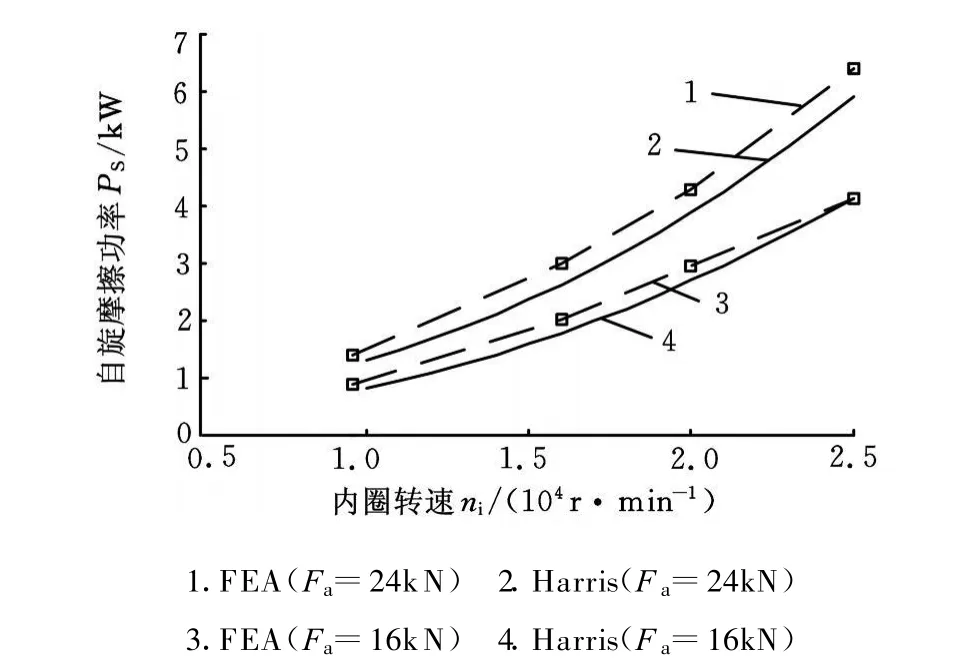
图6 轴承自旋摩擦功率随内圈转速变化(μ=0.05)

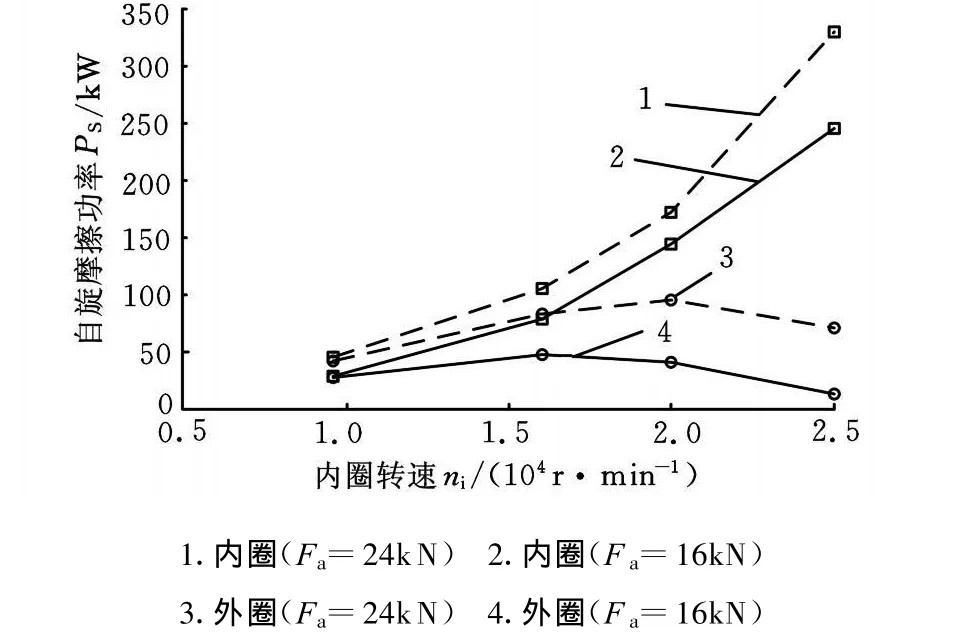
图7 单球自旋摩擦功率随内圈转速变化(μ=0.05)

3 结论

(1)轴向载荷从16kN到24kN、内圈转速从10 000r/min到15 000r/m in,球在内外圈的旋滚比、自旋摩擦功率分别大致相等,分析高速混合球轴承滑动与自旋摩擦功率时不宜忽略球在外圈的旋滚比。Harris拟静力学理论对整个轴承的自旋摩擦功率的估计值偏小。

(2)对于高速混合陶瓷角接触球轴承,适当增大轴向预载可以显著减小球-内圈旋滚比。

(3)摩擦因数对球公转和自转角速度、俯仰角、内外圈旋滚比的影响不大。

[1] Jones A B.A General Theory for Elastically Constrained Ball and Radia l Roller Bearings under A rbitrary Load and Speed Conditions[J].ASM E Journal of Basic Engineering,1960,82(2):309-320.

[2] H arris T A.Rolling Element Bearing Dynam ics[J].W ear,1973,23(3):311-337.

[3] Boness R J,Chapman J J.Measurement and Analysis of Ball Motion in H igh Speed Deep G roove Ball Bearings[J].Trans.of ASM E,Journal of Lubrication Technology,1975,97(3):341-349.

[4] Boness R J.M inimum Load Requirements for the Prevention o f Skidding in H igh Speed Thrust Loaded Ball Bearings[J].Trans.of ASME,Journal of Lubrication Technology,1981,103(1):35-39.

[5] A ltintas Y,Cao Y.V irtual Design and Op tim ization ofMachine Tool Spind les[J].CIRPAnnals-Manufacturing Technology,2005,54(1):379-382.

[6] Chen J S,Hwang Y W.Centrifugal Force Induced Dynam ics of a Motorized High-speed Spindle[J].International Journal o f Advanced Manu facturing Technology,2006,30(1/2):10-19.

[7] A lfares M A,Elsharkawy A A.Effects of Axial Preloading of Angu lar Contact Ball Bearings on the Dynamics of a Grinding Machine Spind le System[J].Journal of Materials Processing Technology,2003,136(1/3):48-59.

[8] Antoine JF,Abba G,Molinari A.A New Proposal for Exp licit Ang le Calcu lation in Angu lar Contact Ball Bearing[J].Journal of Mechanical Design,2006,128(2):468-478.

[9] Jed rzejew ski J,Kw asny W.Modelling o f Angu lar Contact Ball Bearings and Axial Displacements for H igh-speed Spindles[J].CRIP Annals-Manufacturing Techno logy,2010,59(1):377-382.

[10] Liao N T,Lin JF.Ball Bearing Skidding under Radial and Axial Loads[J].Mechanism and Machine Theory,2002,37(1):91-113.

[11] Liao N T,Lin J F.Rolling-sliding Analysis in Ball Bearing Considering Thermal Effect[J].Tribo logy Transactions,2006,49(1):1-16.

[12] W alters C T.The Dynam ics of Ball Bearings[J].Trans.ASME,Journal of Lubrication Technology,1971,93:1-10.

[13] Gupta P K.The Dynam ics of Rolling Element Bearings,PartⅢ:Ball Bearing Analysis[J].T rans.of ASME,Journal of Lubrication Technology,1979,101(3):312-318.

[14] Gup ta P K.Dynamics of Ro lling-element Bearings,Part IV:Ball Bearing Results[J].Trans.of ASME,Journal o f Lubrication Techno logy,1979,101(3):319-326.

[15] Meeks C R,Ng K.The Dynam ics of Ball Separators in Ball Bearings-Part I:Analysis[J].ASLE Transaction,1985,28(3):277-287.

[16] Meeks C R,Ng K.The Dynam ics of Ba ll Separators in Ball Bearings-Part II:Results o f Op tim ization Study[J].ASLE Transaction,1985,28(3):288-295.

[17] Meeks C R,Tran L.Ball Bearing Dynamic Analysis Using Computer Methods-Part I:Analysis[J].Journal of Tribo logy,1996,118(1):52-58.

[18] Stacke L E,Fritzson D.Dynamic Behaviour of Rolling Bearings:Simu lations and Experiments[J].Proceedings o f the Institution of Mechanica l Engineers Part J-Journalof Engineering Tribology,2001,215(6):499-508.

[19] Ghaisas N,Wassgren C R,Sadeghi F A.Cage Instabilities in Cy lind rical Ro ller Bearings[J].T rans.of ASM E,Journal of Tribology,2004,126(4):681-689.

[20] W einzap fel N,Sadeghi F.A Disc rete Element App roach for Modeling Cage Flexibility in Ball Bearing Dynam ics Simulations[J].Journal of T ribology,2009,131(2):021102-11.

[21] Ashtekar A,SadeghiF,Stacke L E.Surface Defects Effects on Bearing Dynam ics[J].Proceedings o f the Institution o f Mechanical Engineers Part JJournalof Engineering Tribology,2010,224(1):25-35.

[22] Harris T A.Rolling Bearing Analysis[M].5th ed.New York:Wiley,2006.

Predicting Skid and Spin Power Loss in a High Speed Hybrid Ball Bearing

Yu Wei1Ren Chengzu1Liu Shengchao2Wang Dongfeng2
1.Key Laboratory of Advanced Ceram ic and Machining Technique,M inistry of Education,Tianjin University,Tianjin,300072 2.Luoyang Bearing Science&Technology Co.,Ltd.,Luoyang,Henan,471039

The rapid ly increased heat generation of high speed hybrid ballbearing draw sa need of p redicting skid and spin power loss of the bearing.A hybrid dynam ic finite element m ethod was p roposed to sim ulate high speed hybrid ball bearings.The resu lts show that w hen axial load varies from 16kN to 24kN and shaftspeed varies in a large range,the spin-to-roll ratio and the spin power lossof outer race is close to that of inner race.It is not appropriate to ignore the spin-to-roll ratio of outer race w hen predicting the skid and spin power loss of the bearing.A proper preload m ay decrease the spin-to-roll ratio of inner race efficiently.

high speed hybrid ball bearing;skid;spin power loss;finite elementmethod

TH 133.334

1004—132X(2011)06—0715—05

2010—05—27

国家自然科学基金资助项目(50975198)

(编辑 苏卫国)

喻 炜,男,1984年生。天津大学机械学院博士研究生。研究方向为混合陶瓷球轴承分析与优化设计。任成祖,男,1962年生。天津大学机械学院教授、博士研究生导师。刘胜超,男,1985年生。洛阳轴研科技股份有限公司助理工程师。王东峰,男,1980年生。洛阳轴研科技股份有限公司工程师。