基于非抽样contourlet变换的图像增强方法

李 艳，杜宇人，沈 鑫

（扬州大学 信息工程学院，江苏 扬州 225127）

图像增强是指有目的地强调图像的整体或局部特征，突出感兴趣的特征，以满足某些特殊分析的需要.目前，图像增强的方法主要有基于空间域和频率域的.基于空间域的算法包括灰度直方图均衡［1－2］、高斯滤波算法、拉普拉斯变换等，这些方法在对图像增强的同时，也增强了噪声信号，故不利于图像的后期处理；而基于频率域的算法是将图像由时域变换到频域，然后通过修正频域内的系数达到增强图像的目的，其中代表性算法有小波变换［3－4］和基于contourlet变换的算法［5－6］等；然而，它们都缺乏平移不变性，会产生伪Gibbs失真.CUNHA等提出的非抽样contourlet变换［7－8］克服了上述算法的缺陷，不仅具有多分辨率和时频局部特性，而且还有很强的多方向选择性和各向异性.本文提出了一种基于非抽样contourlet变换的图像增强算法，算法通过变换系数来确定阈值和分类进行非线性变换.该方法增强后的图像突出了边缘细节，有效抑制了噪声，在视觉效果和对比度评估指标上均明显优于直方图均衡化、小波变换增强方法.

1 非抽样contourlet变换

非抽样contourlet变换（NSCT）的具体步骤为：首先由非抽样塔状滤波器（NSP）将图像分解为低频部分和高频部分，然后由非抽样方向性滤波器组（NSDFB）对高频部分进行若干个方向的分解.NSP是一种平移不变性的双通道滤波器结构，它使非抽样contourlet变换具有多尺度性质，其频域分解图如图1（a）所示.NSDFB由双通道的非采样滤波器组迭代构成，也具有平移不变的特性，它可以将第一级变换得到的高频部分分解为2的任意次幂个方向，且每个方向上的高频部分和低频子带均与原始图像有相同的大小.NSDFB的频域分解图如图1（b）所示.

NSP与NDFB可以保证信号完全重建的条件是滤波器必须满足下式：

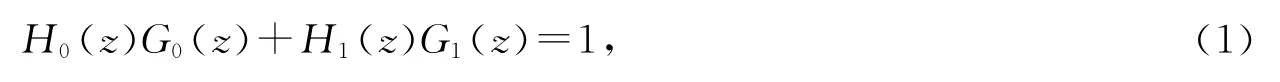
其中 H0（z），H1（z）表示分解滤波器，G0（z），G1（z）表示重建滤波器.非抽样contourlet变换在表达图像时不仅具有contourlet变换所有的优点，而且还具有平移不变性.

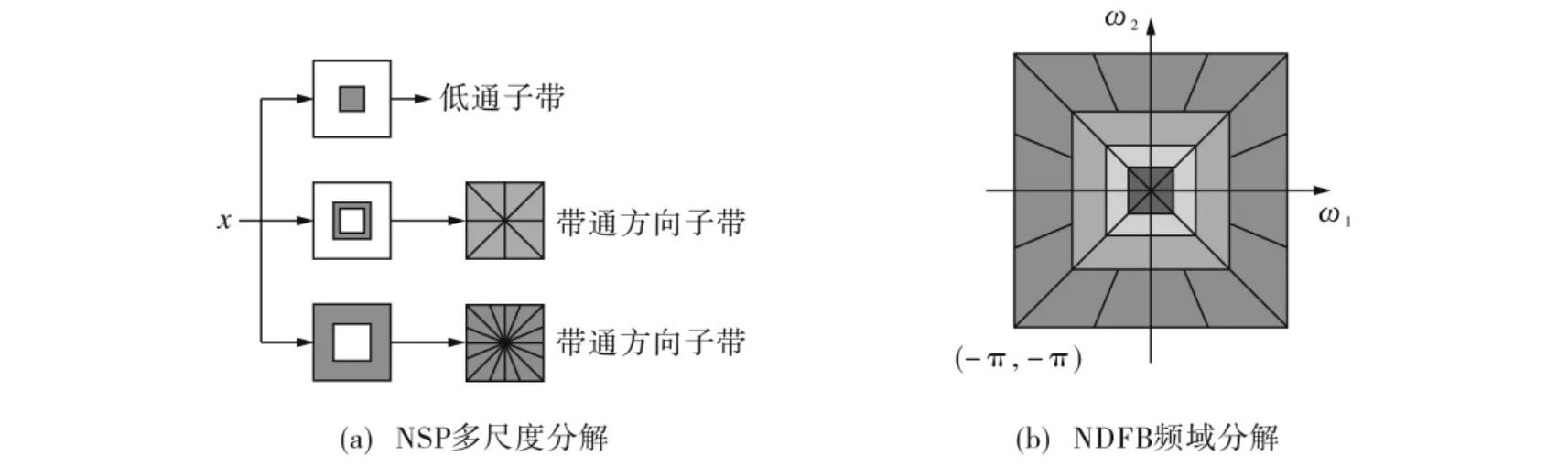
图1 非抽样contourlet变换Fig.1 The nonsubsampled contourlet transform：（a）Nonsubsampled filter bank structure that implements the NSCT，（b）The idealized frequency partitioning obtained with the proposed structure

2 基于非抽样contourlet变换的增强原理

图像经过非抽样contourlet变换后的低频和高频系数可以进行如下分类：低频子带中包含图像的能量信息；高频子带中有较大值的系数对应图像的明显边缘信息；微弱细节信息对应的系数在某些高频子带中有较大的值，而在另一些高频子带中的值较小；在所有高频子带中噪声对应的系数值都较小.

以实验图中的标尺刻度图为例，对其进行NSCT一层分解的结果如图2所示.

图2 非抽样contourlet变换的分解结果图Fig.2 Decomposition result of the image based on NSCT：（a）The image of low frequently in level 1，（b）The image of horizontal high frequently in level 1，（c）The image of vertical high frequently in level 1

基于图2和对以上系数分类信息的分析，可以发现低频子带图的像素对比度低，而高频子带图中含有丰富的边缘信息和噪声，因此可以选择对低频和高频子带系数分别进行非线性处理，以达到增大像素对比度、保持明显边缘信息、提高微弱细节信息及去除噪声的目的.

2.1 低频和高频系数非线性增强

由于图像能量集中在低频子带，但对比度较低，因此本文选择对低频子图进行自适应直方图均衡化处理，以提高像素的对比度.

通过上述分析可以知道，分解后的高频子带含有大量的噪声和边缘信息，因此可以先通过设定阈值对NSCT分解的高频系数进行分类，然后对分类的系数进行不同的非线性处理.本文的阈值δij采用经典中值估计得到：δij＝median（｜cij｜）／0.674 5，其中cij是i层和j方向的高频系数.δij代表i层和j方向的噪声方差.利用该阈值对NSCT分解的高频系数［9］进行分类：

其中x为高频系数，l是对微弱边缘增强的系数（其中0＜l＜1），l越小表示增强的幅度越大，经过试验，本文选择l＝0.3.由式（3）分析可见：通过对分类系数进行非线性处理，图像的明显边缘得到保留，弱边缘得到增强，噪声被有效抑制.

2.2 改进算法步骤

由于光照不均的原因，图像的某些细节会受到影响.假设一幅受到光照影响的图像可由照度I与物体反射光强度R的乘积来决定，即F＝I×R.对上式进行对数运算，得到lg F＝lg I＋lg R，即F′＝I′＋R′，其中F′≈lg F，I′≈lg I，R′≈lg R.对数变换可以降低亮度像素，提高暗像素，从而降低光照不均对图像的影响.

经过非抽样contourlet变换后的图像可分为低频和高频子图像.低频子图像是原图像的近似表示，并且几乎包含了原图像的照度分量I，而反射光强度分量R包含在高频子图像中.由于照度分量在空间上具有缓慢变化的性质，因此为了增加对比度，有必要在包含反射光强度分量的高频子图像中进行处理.结合以上分析，得到本文非抽样contourlet图像增强的具体步骤：

1）对待处理的图像进行对数变换，即F′＝lg F；

2）将对数变换后的图像进行非抽样contourlet变换，得到不同尺度、不同方向的低频和高频变换系数；

3）对低频子图进行自适应直方图均衡，按照公式（2）和（3）原则对分解的高频系数进行非线性处理，得到增强后的系数；

4）由修正后的变换系数重建增强图像.

3 仿真结果和分析

为了检验本文算法的优越性，采用不同算法对实验图像进行增强比较，结果如图3所示，其中本文采用的图像增强方法取k＝4，q＝0.3.

观察实验结果图3可得：本文算法视觉效果好，相对于直方图均衡算法和小波算法，不仅削弱了不均匀光照对图像的影响，而且保留了纹理信息，增强了边缘细节，降低了图像边缘和背景的粘连.

用定量的方法评价图像的增强效果时，本文采用信噪比Rsn进行评价，其定义如下：

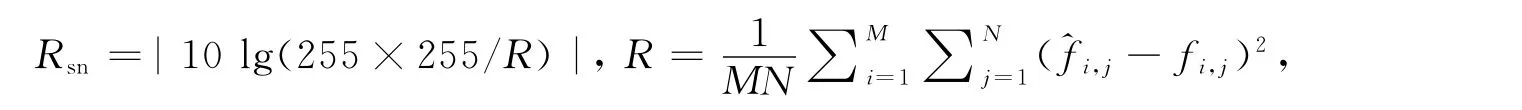
其中fi，j为原始图像各像素灰度值，i，j为重建恢复后各像素灰度值，M，N分别为图像的长度和宽度.由表1可见：本文算法增强后图像的信噪比较其他算法的信噪比都要大，而Rsn值越大，说明去噪效果越好，一定程度上可以表明图像被增强的程度越大.

表1 各增强算法的信噪比Tab.1 The signal－to－noise ratio of various algorithm

为了进一步说明本文算法的优越性，从本文算法增强图像的目的出发，对不同算法增强后的图像进行传统Otsu算法［10］分割，结果如图4所示.

图3 三种增强算法实验比较Fig.3 The comparison of three kinds of enhancement algorithms：（a）The image with ruler scale，（b）and（f）Images enhancement with histogram－equalized，（c）and（g）Images enhancement with wavelet，（d）and（h）Images enhancement with the proposed method in the paper，（e）The image with grid scale

图4 三种增强算法后的二值化实验结果比较Fig.4 The comparison of binary results after three kinds of enhancement algorithms：（a）and（d）Binary images after histogram－equalized，（b）and（e）Binary images after wavelet，（c）and（f）Binary images after the proposed method in the paper

从二值化的实验结果看，对用直方图均衡算法和小波变换算法增强后的图像进行传统Otsu二值化后，图像中出现较多的边缘和背景的粘连，分割效果差；而本文算法增强后的图像二值化效果佳，能将图像的基本纹理和轮廓有效地分割出来；因此，本文增强算法优于直方图均衡算法和小波变换算法.

4 结论

本文的图像增强方法能够利用实验图像的几何本质特征，突出边缘细节，有效抑制噪声信号.实验结果表明：本文算法的信噪比明显提高，图像视觉有较大改善；在主观视觉效果和客观评价方面均优于直方图均衡化算法和小波变换算法；但本文算法仍存在一定的局限性，当图像的噪声方差达到一定值时，对原图像非抽样contourlet变换分解出来的子带系数中弱边缘和噪声的区分难度将加大，很难得到一个较好的阈值进行有效分类，因此会出现伪边缘现象.

［1］CHEN H O，ISA N A M.Quadrants dynamic histogram equalization for contrast enhancement［J］.IEEE Trans Consum Electron，2010，56（4）：2552－2559.

［2］KIM M，CHUNG M.Recursively separated and weighted histogram equalization for brightness preservation and contrast enhancement［J］.IEEE Trans Consum Electron，2008，54（3）：1389－1397.

［3］TANG Jin－shan，LIU Xiao－ming，SUN Qing－ling.A direct image contrast enhancement algorithm in the wavelet domain for screening mammograms［J］.IEEE J Sel Top Sign Process，2009，3（1）：74－80.

［4］DEMIREL H，ANBARJAFARI G.Satellite image resolution enhancement using complex wavelet transform［J］.IEEE Geosci Remote Sens Lett，2010，7（1）：123－126.

［5］董鸿燕，李吉成，沈振康.基于Contourlet变换的带噪图像增强方法 ［J］.信号处理，2007，23（6）：836－840.

［6］DO M N，VETTERLI M.The contourlet transform：an efficient directional multiresolution image representation［J］.IEEE Trans Image Process，2005，14（12）：2091－2106.

［7］雷浩鹏，李峰.基于多小波－非采样Contourlet变换的自适应阈值图像去噪方法 ［J］.计算机应用，2010，30（5）：1351－1355.

［8］ZHOU Jian－ping，CUNHA A L，DO M N.Nonsubsampled contourlet transform：construction and application in enhancement［C］／／Proceedings of the 2005International Conference on Image Processing.Genoa，Italy：IEEE，2005，1：469－472.

［9］MA Yu－xin，XIE Jian－cang，LUO Jun－gang.Image enhancement based on nonsubsampled contourlet transform［C］／／Proceedings of the Fifth International Conference on Information Assurance and Security.Washington DC：IEEE Computer Society，2009，1：31－34.

［10］吴震宇，杜宇人，师文，等.一种基于模糊熵的水凝胶图像分割算法 ［J］.扬州大学学报：自然科学版，2010，13（2）：65－69.