随机结构的单源随机向量表达

汤保新，刘 平

（扬州大学 建筑科学与工程学院，江苏 扬州 225127）

20世纪70年代，SHINOZUKA等学者［1］较为系统地研究了采用随机模拟方法进行随机结构分析的途径；但是，随机变量的数目过多，计算量过大，一直是制约随机分析发展的瓶颈.为此，SUN［2］采用正交展开的方法研究了随机结构分析；李杰等［3－4］独立发展了一类次序正交分解的思想，提出了扩阶系统方法.采用正交分解的方法，随机结构的基本随机变量数目可按近似程度要求适当减少，但随机模拟方法的计算量仍然很大.［5］近年来，有关随机结构分析方法的研究在各个领域继续深入展开［6－11］.在本文中，笔者定义了单源随机向量，仅需一个基本随机变量就可表达随机结构，从而为随机分析开辟了一条新的思路.

1 单源随机向量

所谓单源随机向量，是指以同一个随机变量为自变量的一组随机函数的集合.这里构造一组单源随机向量：

式中θ为［－π，π］上均匀分布的随机变量，α为任意确定的常量.容易推导出ηk（k＝1，2，…，n）的概率密度函数形式相同，均为

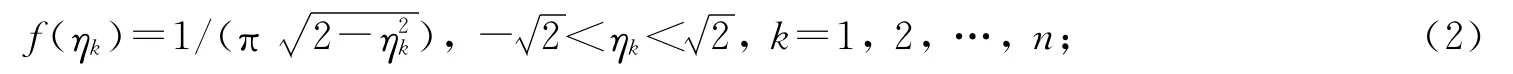
概率分布函数为

由此可见，η的各分量服从同一分布，而且可以证明各分量之间相互独立.

2 用单源随机向量表达实际的随机向量

用单源随机向量表达实际的随机向量需要进行3次变换，变换流程见图1.在流程图中，步骤①是为后续变换作准备，步骤②是变换的基础（见式（1）），步骤③和⑤是两次等概率变换，步骤④是正交线性变换.下面具体阐述变换方法.

图1 3次变换的流程图Fig.1 Flow chart triple transform

2.1 实际随机变量与相关的标准正态分布向量之间的变换

这里先阐述步骤①，步骤⑤是步骤①的逆过程.设结构系统的全部随机变量组成的n维随机向量为ζ＝［ζ1，ζ2，…，ζn］T.如果知道ζ的联合分布函数G（ζ），则可采用Rosenbatt变换［12］，得到独立的标准正态分布向量，但实际上难以知晓，这里不再讨论.而在一般情况下，只知ζ各分量的边缘分布函数为Gk（ζk），k＝1，2，…，n，相关系数矩阵为r，这时可采取 Nataf等概率变换［12－13］，

式中Φ为n维标准正态分布函数，ω＝［ω1，ω2，…，ωn］T是相关系数矩阵为ρ的标准正态分布向量.对式（4）求逆变换，

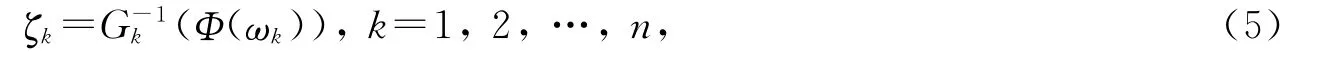
式中G－1k表示反函数.相关系数由下面的积分方程确定：

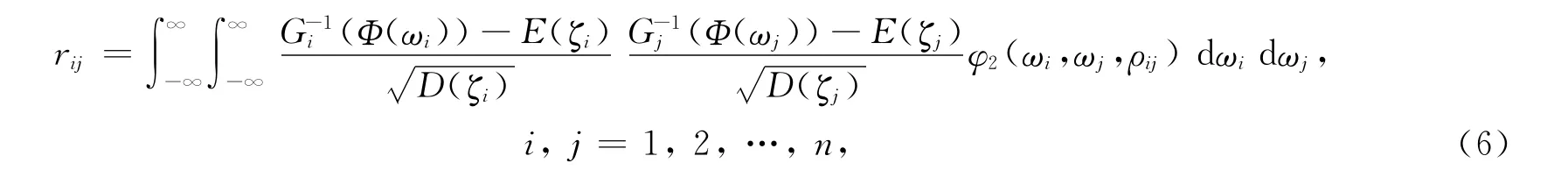
式中E，D分别表示期望值和方差，φ2为2维标准正态分布的概率密度函数，ρij为ωi与ωj的相关系数.

2.2 相关的标准正态分布向量与独立的标准正态分布向量之间的变换

设n维独立的标准正态分布向量为ξ＝［ξ1，ξ2，…，ξn］T.对ω进行线性变换，

式中λ＝diag（λ1，λ2，…，λn）为ρ的特征值矩阵，λk（k＝1，2，…，n）为ρ的特征值，Ψ＝［ψ1，ψ2，…，ψn］为ρ的标准化特征向量矩阵，ψk（k＝1，2，…，n）为列向量.

2.3 独立的标准正态分布向量与单源随机向量之间的变换

再次采用Nataf等概率变换，

对式（8）求逆变换，

式中Φ－1表示反函数.将式（1），（3）代入式（9），得到

至此，得到单一随机变量θ表达的标准正态分布随机向量.

再进行步骤④，⑤的变换，即依次代入式（7）及式（5），可得到由θ表达的随机向量ζ＝［ζ1（θ），ζ2（θ），…，ζn（θ）］T.

3次变换在理论上均为等价变换，可将实际随机变量的数量减少到1个.

3 用单源随机向量表达随机结构

从有限元角度看，随机结构的表达分单元和整体结构两个层次.在单元层次表达之前，须采用单源分析法表达实际结构的基本随机向量ζ.

3.1 实际结构的基本随机向量及其表达

在进行随机分析时，须知晓ζ的边缘概率密度分布和相关矩阵.从数理统计角度考虑，确定随机变量分布密度函数的工作量要比确定其二阶统计量的工作量大得多；所以，在实际工作中，常常采用二阶统计量，并辅以专家经验甚至假定来确定随机变量的分布密度函数.这是一项基础性的工作，影响到随机分析结果的精度和可信程度.

实际结构系统的随机因素都有其物理背景，比如杆件的随机性来源为弹性模量E、截面面积A和截面惯性矩I，而对矩形截面，A和I的随机性来源还可以细分为截面宽度b和截面高度h.通常将不再细分随机性来源的随机变量作为结构系统的基本随机变量，统一编号，记为随机向量ζ＝［ζ1，ζ2，…，ζn］T.对基本随机向量ζ进行单源分析，从而使其每个分量均为θ的函数.

3.2 单元层次上随机函数的正交展开

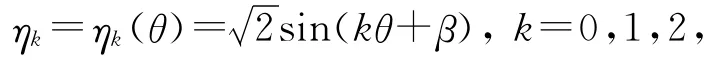
以杆件单元为例，E和A的乘积EA为轴向刚度，E和I的乘积EI为抗弯刚度，它们为基本随机变量E，b，h的函数.已知结构参数E服从正态分布NE（3.0×1010N·m－2，0.5×1010N·m－2），b，h服从对数正态分布LNb（0.25m，0.05m），LNh（0.6m，0.05m），相关系数rbh＝0.3.先对b，h进行单源分析，然后对EA和EI进行正交展开，得到多阶表达式

3.3 随机结构的表达

不失一般性，下面以弹性杆单元为例，阐述单元分析过程.

考察一杆单元.单元编号为e，单元长度le为确定量，单元刚度矩阵为

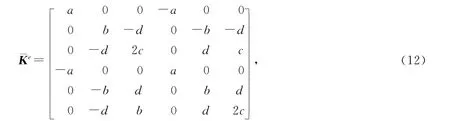
其中a＝EA／le，b＝12EI／，c＝2EI／le，d＝6EI／.经过第3.2节的正交展开，EA和EI是ηk（k＝0，1，2，…）的线性表达式，那么也是ηk（k＝0，1，2，…）的线性表达式，可表示为

与普通有限元过程类似，将单元刚度矩阵的各阶展开矩阵进行旋转，按各阶次组装成整体刚度矩阵，并引入边界条件，可表示为

式中Kk（k＝0，1，2，…）为整体刚度矩阵的第k阶展开项.整体刚度矩阵是一个多阶展开式，结构的随机性完全体现在单源随机向量η中，这样，随机结构最终只须用一个基本随机变量θ表达.根据式（14），可计算结构的概率特征，如常用的一阶、二阶统计量，

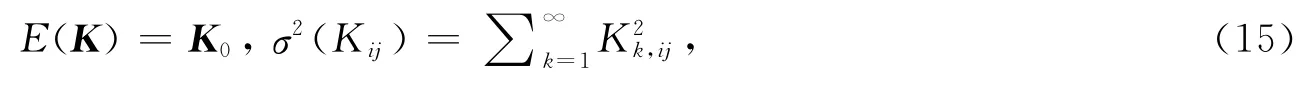
式中Kij，Kk，ij分别为整体刚度矩阵和第k阶展开矩阵的元素.

4 算例

分析一个两杆静定桁架，如图2所示。杆件截面面积为A1，A2，材料屈服强度为fy1，fy2，均为随机变量，随机变量的特征参数见表1。求结构的极限承载力Pu。

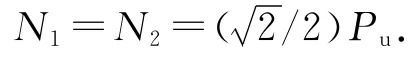
图2 算例的计算简图Fig.2 Calculation diagram

表1 随机变量的特征参数Tab.1 The characteristic parameters of random variables

图3 结构随机变量的变化图Fig.3 The variation diagram of structural random variables

以直接采用蒙特卡罗法求得的结果作为相对精确解，与本算例的计算结果比较见表2.

表2 结构极限承载力计算结果比较Tab.2 Comparison of the calculation results of structural limit bearing capacity N

算例表明：整个结构系统的随机变量最终可只采用一个基本随机变量表达，结构承载力的变化形态也可以直观地观察到，便于研判.

图4 结构极限承载力的变化图Fig.4 The variation diagram of structural limit bearing capacity

［1］SHINOZUKA M，JAN C M.Digital simulation of random processes and its applications［J］.J Sound Vib，1972，25（1）：111－128.

［2］SUN Tze－chien.A finite element method for random differential equationswith random coefficients［J］.J Numer Anal，1979，16（6）：1019－1035.

［3］LI Jie，ROBERTS J B.The expanded order system method of combined random vibration analysis［J］.Acta Mech Sinica，1996，12（1）：66－75.

［4］李杰.随机结构系统：分析与建模 ［M］.北京：科学出版社，1996：128－232.

［5］韩大建，陈太聪，苏成.随机结构数值模拟分析的神经网络法 ［J］.工程力学，2004，21（3）：49－54.

［6］ZHAO Lei，CHEN Qiu.Neumann dynamic stochastic finite element method of vibration for structures with stochastic parameters to random excitation［J］.Comput Struct，2000，77（6）：651－657.

［7］LI Jie，LIAO Song－tao.Response analysis of stochastic parameter structures under non－stationary random excitation［J］.Comput Mech，2001，27（1）：61－68.

［8］SCHUELLER G I.Computational stochastic mechanics－recent advances［J］.Comput Struct，2001，79（22／25）：2225－2234.

［9］王凤阳，赵岩，林家浩.参数不确定结构平稳随机响应虚拟激励摄动方法 ［J］.大连理工大学学报，2011，51（3）：320－325.

［10］ZHUwei－qiu，CAI Guo－qiang，ZHANG Rui－chong.Advances in stochastic structural dynamics：proceedings of the fifth international conference on stochastic structural dynamics［M］.Boca Raton，USA：CRC Press，2003：1－624.

［11］李杰，陈建兵.随机振动理论与应用新进展 ［M］.上海：同济大学出版社，2009：60－103.

［12］张明.结构可靠度分析：方法与程序 ［M］.北京：科学出版社，2009：37－67.

［13］秦权，林道锦，梅刚.结构可靠度随机有限元：理论及工程应用 ［M］.北京：清华大学出版社，2006：20－26.