基于ANSYS的提环有限元分析及优化

蒋 波，赵毅红，王军领，李士佩，李 恒，陈荣发

（扬州大学 机械工程学院，江苏 扬州 225127）

在正常工作状态下，石油钻井设施水龙头的上部与游车大钩保持相对静止，下部与数千米的钻杆连接而实现旋转运动，内部流动有高压液体，其受到扭转、弯曲等多种载荷的作用，受力状态极其复杂.水龙头的提环U形部位内侧面与大钩钩口接触，耳环孔通过柱销与水龙头壳体相连，其结构设计与性能对水龙头的安全使用非常重要.［1］提环是水龙头中最重要的承重部件［2］，提环的强度和刚度满足设计要求是水龙头正常工作的前提.杨晓翔［3］和WRIGHT［4］等分析计算了提环的微裂纹及应力强度因子，LEA等［5］对提环的受载荷部位采用余弦加载进行了探讨；但大部分研究只限于对提环应力和应变的分析，而在此基础上的优化设计方法涉及很少.本文通过有限元分析模拟提环在真实工况下的应力和变形情况，对提环进行结构优化和校核，使其满足强度和刚度要求.

1 实体模型建立

在某企业160t水龙头的设计中，应用Pro／E软件建立了水龙头各零部件的实体模型，并装配成整机，如图1所示.提环、水龙头壳体、中心管等是水龙头的关键零部件，它们的强度和刚度是影响水龙头性能的重要因素.［6］本文仅以提环为例来研究基于ANSYS的有限元分析及优化.在水龙头的实体模型中，可以直接导出提环的实体模型.

图1 水龙头实体模型Fig.1 Entity model of the swivel

2 接触块的计算和加载

为避免接触区求解时所必需的大量迭代运算，根据接触构件的几何形状和尺寸，由接触问题的弹性理论对接触区尺寸及最大应力进行估计后，选择一个适当尺寸的附加接触块与结构相连，在该接触块上施加载荷或适当约束，以代替相关构件对所分析构件的作用.在无滑动情况下，该处理可望获得较为接近实际接触面的应力分布.［3］19提环上部与大钩钩口间接触面形状是较为复杂的曲面接触，可将其简化为柱面接触，示意图如图2所示.

接触面的半宽ω1，ω2可按下列方程联解［3］20：

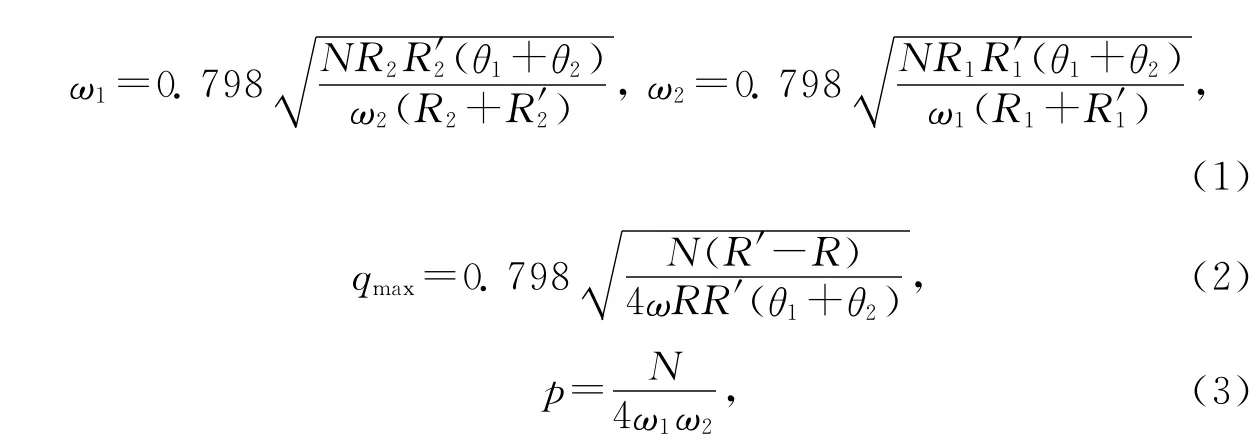
式中N 为提环承受的最大载荷；θi＝（1－）／Ei（i＝1，2），其中Ei和υi分别为接触体的弹性模量和泊松比；qmax为接触区最大应力；R2，R′2和R1，R′1是相互正交的剖面中接触块和提环的半径；p为加载在接触块上的压力.

图2 提环上部与大钩钩口接触示意图Fig.2 Contact diagram of the upper part of the bail and the hook

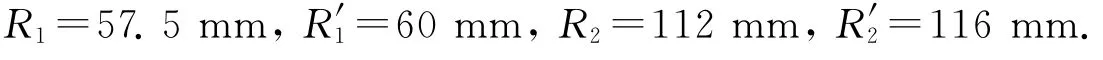
水龙头提环的耳环与柱销是两柱面间的接触，假设接触块与耳环的下部半个柱面都接触，计算中外载荷均匀作用在提环上部接触块上，柱销在载荷方向施以约束，提环接触块加载如图3所示.

3 基于ANSYS的提环分析

3.1 创建有限元模型

通过ANSYS与Pro／E软件的无缝接口，将提环模型导入 ANSYS中.［7－8］选用线性单元SOLID186并采用ANSYS智能划分网格方式，精度为4级.

提环的材料选为35CrMoA，屈服点σs＝835MPa，抗拉强度σb≥985MPa，杨氏模量E＝2.02×105MPa，泊松比υ＝0.3.划分网格后的提环如图4所示.

图3 提环的接触块加载Fig.3 The load of contact block

图4 提环及接触块的有限元模型Fig.4 Finite element model of the bail and contact block

3.2 施加载荷及求解计算

在约束关系上，耳环接触块在x方向施加约束，同时在提环U形部位一对平行面上施加z方向的约束；在提环上部接触块上施加529MPa的压力载荷，在耳环的内侧面上施加6MPa的压力载荷，使U形开口的大小不会变形.施加载荷和约束后ANSYS开始求解.

3.3 结果分析

通过ANSYS后处理器，得到提环在载荷下的等效应力分布图（图5）和等效位移变形分布图（图6）.

由图5可以看出，提环的等效应力主要分布在提环的U形部位内侧、直杆内侧和耳环部位，其中提环U形部位内外侧的应力比较大，同时耳环部位2个轴孔处的应力也较大，最大应力发生在提环U形部位内侧的中间部位，其最大应力值为500MPa，此应力值远小于材料的屈服极限值835MPa和抗拉强度值985MPa.

图5 提环等效应力分布图Fig.5 Equivalent stress distribution of the bail

图6 提环等效位移变形分布图Fig.6 Equivalent displacement deformation distribution of the bail

材料的许用应力［σ1］＝985MPa，计算可得提环的安全系数η＝［σ1］／σ＝985／500＝1.97.根据我国《钻井、采油提升设备规范》规定的屈服设计安全系数为2.25（最大载荷大于150t）［9］，略大于目前得到的安全系数1.97.本文计算结果表明：提环设计的强度不能完全满足使用要求.

由图6可以看出，提环的位移变形沿着直杆中间偏上的部位向上、下两端逐渐减小，并且在直杆的这一部位产生最大位移，变形量为1.575mm.根据《钻井和采油提升工具通用技术条件》规定：经最大试验载荷试验的提升工具，除接触区外变形量不得超过0.2%，提环总长1 435mm，计算可得其变形量为0.1%，在规定范围内，位移变形能够满足提环的工作要求.

4 提环的优化

传统的设计理论和方法通常是运用一些经验公式或者通过估算来计算产品的设计参数，但有可能导致设计的安全系数因为某种原因达不到正常工作的要求.［10－13］本文通过增大提环U形部位圆截面直径和耳环孔径进行优化.图7和图8分别为圆截面直径增大3mm，耳环孔径增大4mm后得到的优化提环等效应力分布图和等效位移分布图.

图7 优化提环等效应力分布图Fig.7 Equivalent stress distribution of the bail after optimization

图8 优化提环等效位移分布图Fig.8 Equivalent displacement deformation distribution of the bail after optimization

由图7可以看出，优化后提环的等效应力分布范围和渐变趋势与原壳体的应力分布大致相同，最大等效应力发生在耳环圆孔处，其值为435MPa，小于材料的屈服极限和抗拉强度值.新的安全系数η＝985／435＝2.26，计算结果表明优化后的提环在强度上已能够满足设计要求.由图8可以得出，提环的最大变形量大约在直杆中间偏上部位，最大变形量与原提环的变形量相比，减少了0.127mm，优化后变形量最大值为1.448mm，能够满足设计要求.

综上所述，对提环优化后，其强度要求已得到满足，同时使变形量减少了8%，提环的刚度有了较大改善，这对提升水龙头装置的工作性能具有重要意义.

［1］薛明晋，陈海林，夏美忠，等.SL225型水龙头提环的应力与变形有限元分析 ［J］.石油矿场机械，2009，38（3）：36－38.

［2］陈海林，薛明晋，夏美忠，等.基于Pro／E和ANSYS的提环实体建模与有限元分析 ［J］.石油矿场机械，2008，37（12）：19－21.

［3］杨晓翔，李中华，张毅，等.SL450水龙头提环三维有限元分析 ［J］.石油机械，1995，23（2）：19－23，48.

［4］WRIGHT Dw，ADAIR R L.Progressive cavity pumps prove more efficient in mature water flood tests［J］.Oil Gas J，1993，91（32）：43－47.

［5］LEA J F，ANDERSON P O.Optimization of progressive cavity pump systems in the development of the clear water heavy oil reservoir［J］.J Can Pet Technol，1988，27（1）：58－67.

［6］李宏伟，杨成.基于ANSYS的内啮合齿轮泵壳体有限元分析及优化 ［J］.液压与气动，2011（2）：32－35.

［7］PIDAPARTI R M，JAYANTI S，HENKLE J，et al.Design simulation of twisted cord－rubber structure using ProE／ANSYS［J］.Compos Struct，2001，52（3／4）：287－294.

［8］郑翔，方开荣，王成，等.四缸柴油发动机机体有限元模态仿真及其测试 ［J］.扬州大学学报：自然科学版，2010，13（1）：42－46.

［9］张益诚.200吨水龙头提环三维有限元弹塑性应力分析 ［J］.甘肃工业大学学报，1985，11（2）：47－55.

［10］KALYANASUNDARAM S，LOWE A，WATTERS A J.Finite element analysis and optimization of composite wheelchair wheels［J］.Compos Struct，2006，75（1／4）：393－399.

［11］CAO Pin－lu，YIN Kun.Optimization design and finite element analysis of core cutter［J］.J Chin Univ Min Technol，2007，17（3）：399－402.

［12］AVILES R，VALLEJO J，AGUIRREBEITIA J，et al.Optimization of linkages for generalized rigid－body guidance synthesis based on finite element models［J］.Finite Elem Anal Des，2010，46（9）：721－731.

［13］KONNO J，STENBERG R.Finite element analysis of composite plates with an application to the paper cockling problem ［J］.Finite Elem Anal Des，2010，46（3）：265－272.