风电机组塔筒模态的环境脉动实测与数值模拟研究
马人乐,马跃强,刘慧群,陈俊岭
(同济大学 土木工程学院建筑工程系,上海 200092)
风电机组塔筒模态的环境脉动实测与数值模拟研究
马人乐,马跃强,刘慧群,陈俊岭
(同济大学 土木工程学院建筑工程系,上海 200092)
基于随机振动及系统识别理论,对内蒙古京能乌兰伊利更风电场中三座风电机组塔筒进行了环境脉动实测,提出了“桨叶—轮毂—机舱—塔筒”耦合的整体建模的方法,数值模拟与实测结果表明,风电机组塔筒可以有效地避免共振,满足GL规范的设计要求;塔筒主要振动形式为侧向弯曲振动、前后弯曲振动和扭转振动;塔筒一阶平动阻尼比为1.78%左右,一阶扭转阻尼比为0.6%左右。采用整体建模方法建立的模型与实测结果有较好的一致性,可以指导风力发电塔系统的风致动力响应分析和振动控制分析。
风电机组塔筒;环境脉动实测;模态分析;频率;阻尼比;整体建模
风电机组工作时,当桨叶旋转产生的激励频率或通过频率接近塔筒的固有频率,塔筒将产生较大的振动,甚至发生共振,使塔筒产生较大的动应力,并产生较大的疲劳应力幅,缩短整机的使用寿命,甚至导致整机无法工作[1]。随着风电机组向大型化发展,结构柔度增加,风电机组塔筒的动力特性日益受到关注。
目前,风电机组塔筒模态的研究多采用基于分析力学[2-3]、多体动力学[4-5]和有限元的理论方法[6-7]。Thomas[8]等在实验室对一个垂直型风电机组模型在停机和运行状态下进行了模态测试,得到了相应的频率及其阻尼比。但风电机组塔筒通常处在恶劣多变的自然环境中,并且在高耸塔筒的顶端安装有截面形状复杂的叶轮、机械装置及其附属配件,很难通过理论方法和实验模型准确地得到结构的模态,因此现场实测便成为获得风电机组塔筒模态较为可靠的方法,但模态的现场实测研究国内外文献鲜有报告。GL规范和国内风电机组相关规范都要求对塔筒进行动力计算,但都没有给出相应模态阻尼比的建议值。另外,目前风力发电塔系统有限元建模多采用将桨叶和机舱凝聚成塔顶的质量块的简化处理方法[9],但此方法无法准确体现桨叶与塔筒的耦合机制,也无法体现桨叶的振动形式,桨叶与塔筒之间相互作用的不确定性也可能带来经济上的浪费或者安全上的隐患,其合理性有待进一步研究。Murtagh等[7]提出了一种基于剪力传递的桨叶和塔筒的耦合机制,虽然考虑桨叶和塔筒之间的耦合,但忽略了两者之间弯矩、扭矩和轴力的传递。
本文首先基于随机振动系统识别理论[10],对内蒙古京能乌兰伊利更风电场中三座风电机组进行环境脉动实测,得出塔筒的固有频率及其阻尼比,为建立风力发电塔系统的有限元模型提供第一手资料。然后,依据风力发电塔系统不同构件的特点,并在已有模型的基础上[7,9,11,12],提出了“桨叶 - 轮毂 - 机舱 - 塔筒”耦合的整体建模的方法,分析了风力发电塔系统的模态,获得了塔筒的固有频率和振型。数值分析与实测结果对比表明,本文提出的风力发电塔系统整体建模的方法可行,可以指导风力发电塔系统风致动力响应分析和振动控制分析。
1 工程背景及实测方案
1.1 工程背景
测试的风电机组位于内蒙古京能乌兰伊利更,平均海拔高度为1 380 m,主导风向为西南风,安装200台1 500 kW/77直驱式风电机组,轮毂高度为65 m,叶轮直径为77 m,额定转速为17.3 r/min,选其中三台风电机组N53、N65和N73开展实测。
1.2 测试方法及测点布置
假定X为沿机头方向,Y为垂直于机头方向,Z为竖向。布置8个测点,测点1、5和7沿X方向布置,测点2、6和8沿Y方向布置,测点3和4平行X方向布置,测点对应布置在平台二、平台三和平台四,测点布置见图1~图3。测试时采用LC0132型内装IC压电式加速度传感器来测试塔筒的加速度时程曲线,传感器通过其自带吸铁吸附于塔筒内壁和耳板上。采用SVSA软件进行数据采集,采样频率为50 Hz,采样长度为9 216,现场数据采集见图4。
2 实测数据分析与处理
2.1 分析方法
风电机组塔筒测试为既有地面脉动又有风载的多输入系统,在输入信号未知的情况下直接利用风电机组塔筒的脉动响应信号识别模态参数[13-15]。通过功率谱曲线上的峰值点得到系统整体振动的固有频率。由于可能存在局部共振,因此需要从同方向结构上各测点的功率谱曲线综合分析判断。文中采用半功率点法确定阻尼比。

图4 现场数据采集Fig.4 On-site data gathering
对于平动与扭转耦合振动,可通过对称点加速度的加减区分开。将信号相加,可抵消扭转信号,得到两倍平动信号;将信号相减,可抵消平动信号,得到两倍扭转信号。
2.2 测试结果
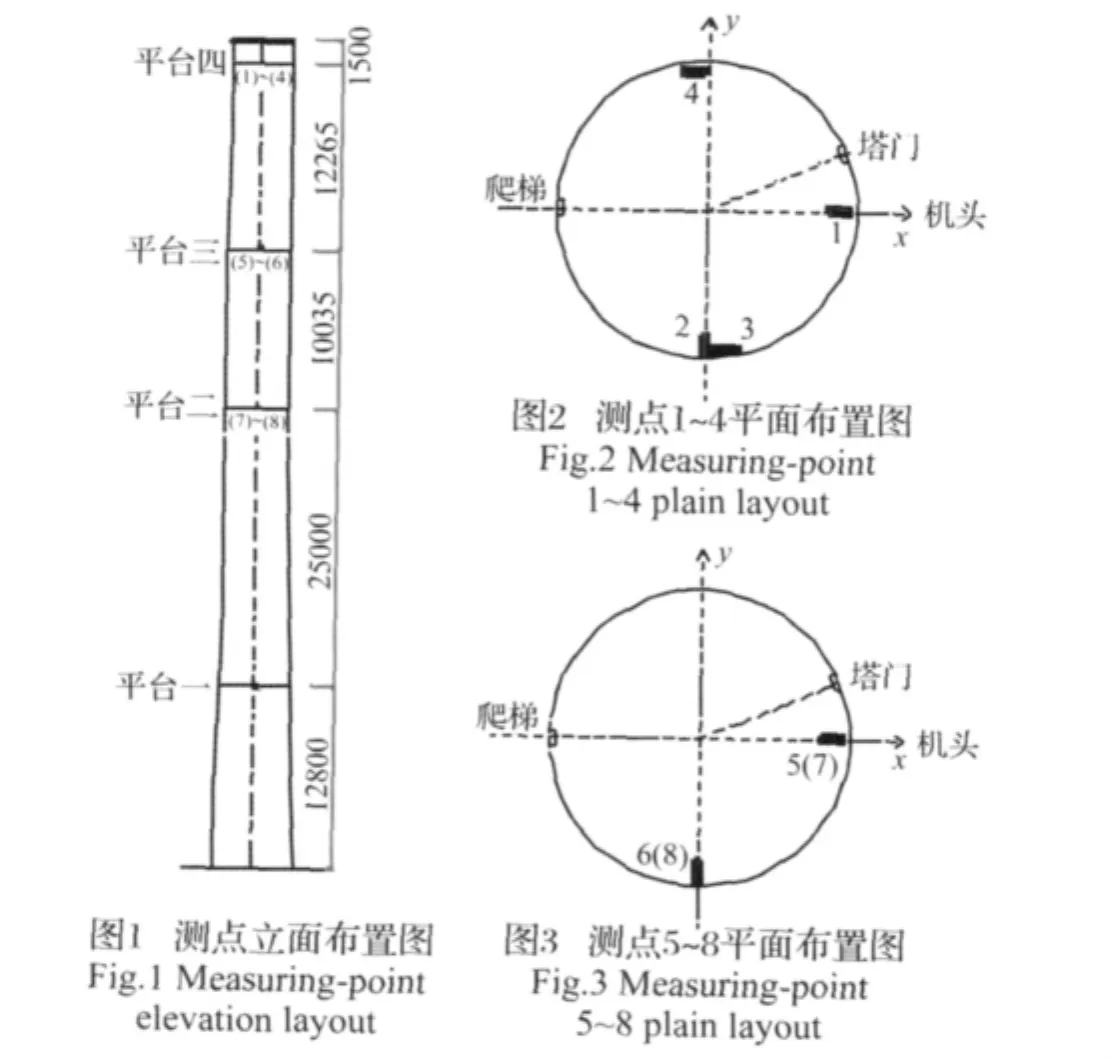
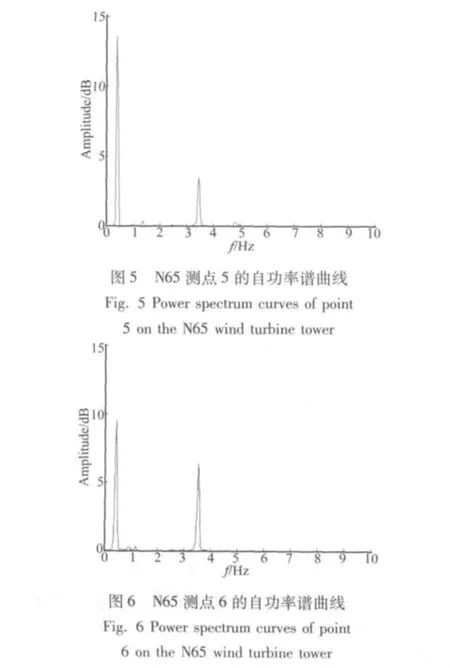
测试可以得到各个测点加速度时程曲线。对测点1、2、5、6、7和8通过频谱分析得到此6个测点的自功率谱曲线,得到塔筒的平动频率及其阻尼比风力发电塔,N65测点5、6的自功率谱曲线分别见图5和图6。
测点3和4的加速度相减,除以两测点之间的距离,然后频谱分析得到塔筒的扭转自功率曲线,得到塔筒的扭转频率及其阻尼比,风力发电塔N65扭转的自功率谱曲线见图7。N53和N73的测试结果与N65基本相同,测试的三座塔筒的前五阶固有频率及其阻尼比测试值见表1。
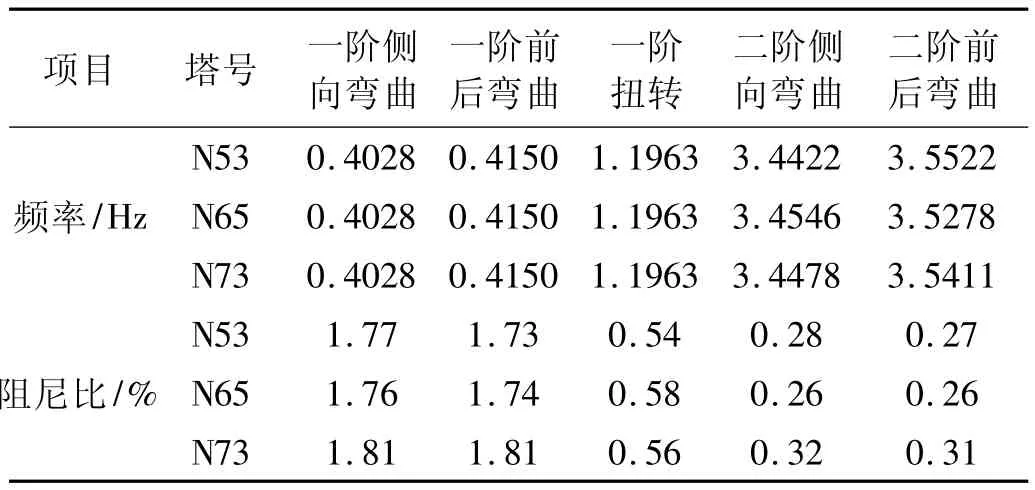
表1 三座塔筒前五阶固有频率及阻尼比测试值Tab.1 Inherent frequencies and damping ratio of the previous five phrases of the three towers
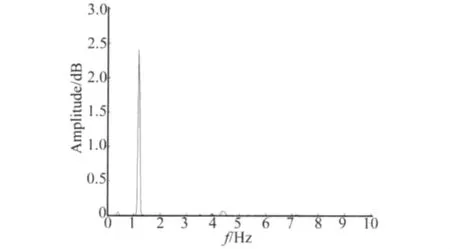
图7 N65扭转的自功率谱曲线Fig.7 Torsional power spectrum curve on the N65 wind turbine tower
由表1可知,三座塔筒的前五阶固有频率和阻尼比数值基本相同,对各组所测频率和阻尼比取平均值,得到本风电机组塔筒的前五阶固有频率为0.402 8 Hz、0.415 0 Hz、1.196 3 Hz、3.441 5 Hz 和 3.505 2 Hz,满足GL规范的设计要求,可以有效地避免共振。
由于GL规范和国内风电机组相关规范中都未给出动力分析时阻尼比的建议值,工程中常采用《高耸结构设计规范》中钢结构阻尼比为1%;由表1可知,一阶平动阻尼比为1.75%左右,一阶扭转阻尼比为0.56%左右,因此风力发电塔系统的平动阻尼比值比一般的高耸钢结构偏大,采用《高耸结构设计规范》建议值并不合适,建议在风力发电塔系统动力分析时采用本文给出的阻尼比值。
3 有限元分析
风电机组主要构件有桨叶、轮毂、机舱和塔筒,它们之间的耦合作用对塔筒的模态有很大的影响[16]。本文依据风电机组主要构件的特点,并在已有模型的基础上,提出考虑“桨叶—轮毂—机舱—塔筒”耦合的整体建模的方法,分析风力发电塔系统的模态,获得塔筒的固有频率和振型。
3.1 风力发电塔系统整体建模
所测风电机组轮毂高度为65 m,由三节塔段构成,塔底直径为4 m,厚度为26 mm,塔顶直径为2.57 m,厚度为12 mm,弹性模量为2.1×1011N/m2,密度为7 850 kg/m3。根据塔筒的几何特征和主要受力特点,采用八节点SHELL181壳体单元。
风电机组叶轮直径为77 m,根据刚度等效原则将不规则的桨叶转化为规则形状,可视为中空矩形的变截面悬臂梁,叶底处的截面为3 m×0.8 m×0.01 m,叶尖处的截面为 0.3 m ×0.08 m ×0.01 m,采用BEAM189单元,叶片材料为玻璃钢,可看作正交各向异性材料,密度为2 100 kg/m3,展向模量为6.25×1010Pa,径向模量为 1.65 ×1010Pa,剪切模量为 5.5 ×109Pa,泊松比为 0.22。
由于机舱和轮毂结构比较复杂,但在整体分析过程中并不需要关注起内部细部特征,因此机舱和轮毂可简化为质量点,采用 mass21质量单元模拟,设置单元参数考虑其质量、质量转动惯量和偏心位置,然后将质量单元节点、塔筒顶部和桨叶通过CERIG命令刚性连接。由于基础相对上部结构刚度很大,可以认为结构底部完全固结,不考虑土体对结构影响[12]。通过以上整体建模的方法,得到本风电机组整体有限元模型,见图8。

图8 风电机组整体有限元模型Fig.8 Overall Model of the Wind Turbine System
3.2 风电机组塔筒模态分析
本文采用Block Lanczos法对风力发电塔系统进行模态分析,得到固有频率和振型[16],其中前十阶的固有频率理论值和振型描述见表2。
由表2可知,风电机组塔筒的振动形式主要表现为侧向弯曲振动、前后弯曲振动和扭转振动,和实测得到的振动形式相同;第一阶和第二阶分别为风电机组塔筒的一阶侧向弯曲振动和一阶前后弯曲振动,频率分别为 0.425 7 Hz和 0.427 5 Hz,叶片振动较小;第五阶时塔筒出现一阶扭转振动,频率为1.232 2 Hz;第九阶和第十阶时塔筒分别为二阶侧向弯曲振动和二阶前后弯曲振动,频率分别为3.457 2 Hz和3.476 9 Hz;其它阶的振型以叶片的振动为主。
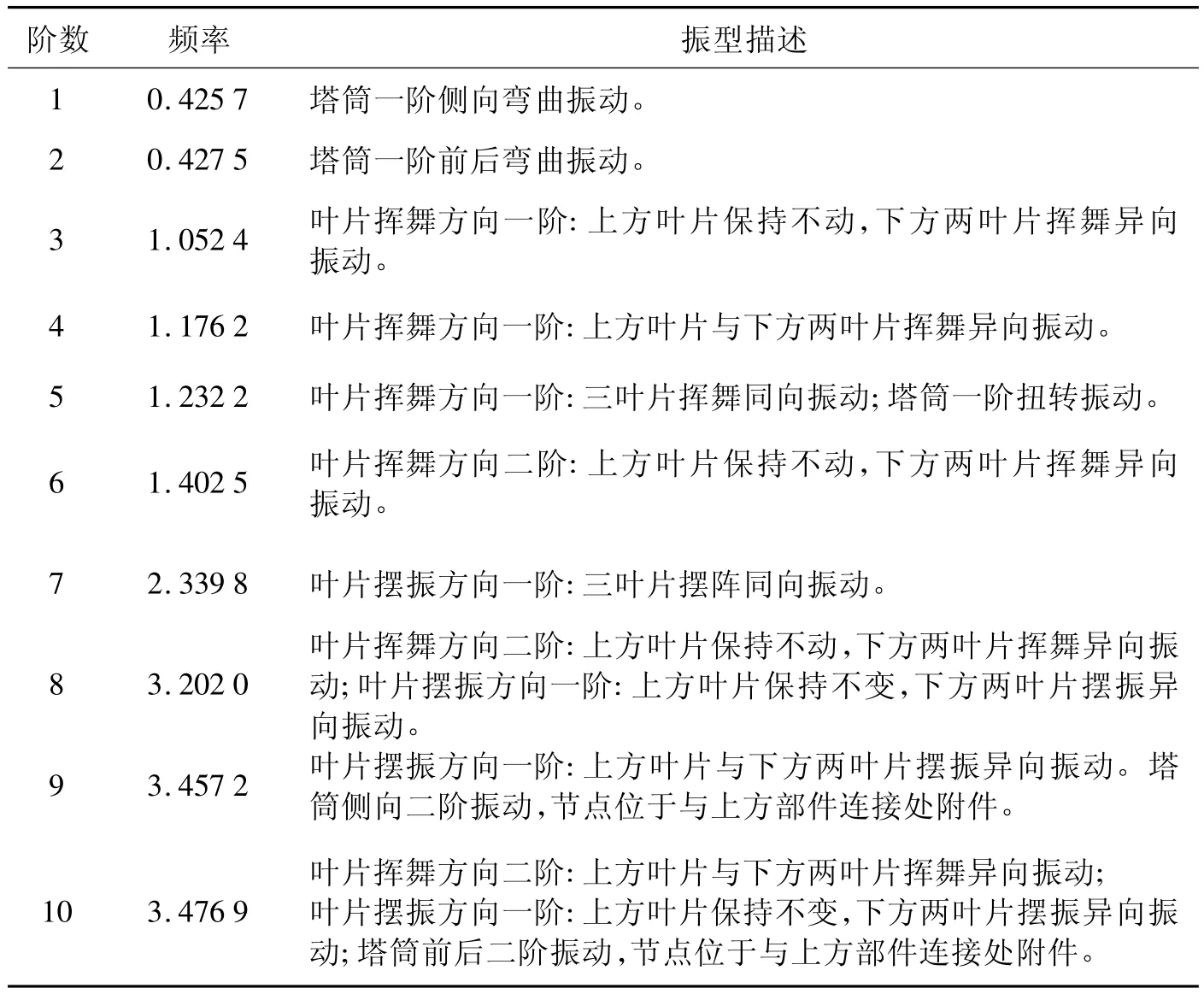
表2 风力发电塔系统前十阶固有频率理论值及振型描述Tab.2 The inherent frequencies and Description of Modes of the previous ten phrases
通过对比可知,塔筒频率理论值比实测值偏高,误差范围基本在5%以内,从工程的观点来看,是可以接受的。产生误差的主要原因是理论模型与实际结构存在一定的差异以及脉动实测本身误差等引起。数值分析与实测结果对比结果表明,本文提出的风力发电塔系统整体建模的方法可行。可以用于风力发电塔系统风致动力响应分析和振动控制的分析研究。
4 结论
通过对风电机组塔筒进行现场实测与数值模拟,得到如下结论:
(1)现场实测所得塔筒的固有频率,满足GL规范设计,可以有效地避免共振;
(2)塔筒主要的振动形式为侧向弯曲振动、前后弯曲振动和扭转振动;
(3)塔筒一阶平动阻尼比为1.7%左右,一阶扭转阻尼比为0.6%左右,可作为风电机组塔筒结构分析时参考;
(4)采用“桨叶-轮毂-机舱-塔筒”耦合的整体建模的方法对风电机组塔筒进行有限元分析,结果可靠,此建模方法可以用于风力发电塔系统的风致动力响应分析和振动控制的分析研究。
[1]Burton T,Sharpe D,Jenkins N.Wind energy handbook[M].New York:John Wiley& Sons,2001.
[2]Miller R H,Dugundig J,Wendell J.Dynamic of horizontal axis wind turbine[R]. Wind Energy Conversion,MIT,ASRL-IR-184 -9,DOE COO- 4131-T1,1978.
[3]Sheu D L.Effects of tower motion on dynamic response of windmill rotor[R]. WindEnergyConversion,VO1 VII,ASRL-IR-184 -13,DOE COO-4131-T1,1978.
[4]Wright A D,Kelley N D,Osgood R M.Validation of a model for a twobLaded flexible rotor system:progress to date[C].Proceedings of the 37thAIAA Aerospace Sciences Meeting and Exhibit, Reno,Nevada,1999:293-307.
[5]Lee D,Hodges D H,Patil M J.Multi-flexible-body dynamic analysis of horizontal axis wind turbines[J].WindEnergy, 2002, (5):281-300.
[6]LobtizD W. A Nanstran-based computerprogram of structural dynamic analysis of horizontal axis wind turbine[C].Proceedings of the Horizontal Axis Wind Turbine Technology Workshop,Department of Energy and NASALewis,Cleveland,1984.
[7]Murtagh P J,Basu B,Broderick B M.Along-wind response of a wind turbine tower with blade couping subjected to rotationally sampled wind loading[J]. Engineering Structures,2005,27(8):1209 -1219.
[8]Thomas G C,Arlo N.Modal testing of a rotating wind turbine[R]. SAND82 - 0631, Sandia: Sandia National Laboratories,1983.
[9]蒋香梅.有限单元法在风力发电机开发中的应用研究[D].乌鲁木齐:新疆农业大学,2002.
[10]俞载道,曹国敖.随机振动理论及其应用[M].上海:同济大学出版社,2000.
[11] Bazeos N,Hatzigeorgiou G D,Hondros I D et al.Static,seismic and stability analysis of a prototype wind turbine stell tower[J].Engineering Structures,2002,24(8):1015-1025.
[12] Lavassas I,Nikolaidis G,Zervas P et al.Analysis and design of the prototype of a stell 1-MW wind turbine tower[J].Engineering Structures,2003,25(8):1097 -1106.
[13]闫祥梅,何敏娟,马人乐.高压输电塔同步环境脉动实测分析与对比[J].振动与冲击,2010,29(3):77-80.
[14]何敏娟,马人乐,黄征.336m高钢结构电视塔模态参数实测与分析[J].同济大学学报,2001,29(7):862-866.
[15] Gentile C A.Ambient vibration testing of historic massonry towers for structural identification and damage assessment[J].Construction and Materials,2007,21:1311 -1321.
[16]贺广零.风力发电高塔系统风致随机动力响应分析与抗风可靠度研究[D].上海:同济大学,2009.
Ambient vibration test and numerical simulation for modes of wind turbine towers
MA Ren-le,MA Yue-qiang,LIU Hui-qun,CHEN Jun-lin
(Department of Building Engineering,Tongji University,Shanghai 20092,China)
Based on the theory of random vibration and system identification,ambient vibration tests of three wind turbine towers in wind-power station of Inner Mongolia Wulanyiligeng were carried out.The method of coupling overall modeling of blade,hub,nacelle and tower was put forward,and the numerical stimulation and tests results showed that the wind turbine towers can effectively avoid resonance,and meet the standard design requirements of Germanischer Lloyd;the vibrational forms of the wind turbine towers mainly are lateral bending vibration,forth-and-back bending vibration and torsional vibration;the translational damping ratio in the first mode is about 1.75%,and the torsional damping ratio in the first mode about 0.6%.The overall modeling showed excellent consistency with the test results,it could benefit wind-induced dynamic response analysis and vibration control analysis of wind turbine tower systems.
wind turbine tower;ambient vibration test;modal analysis;frequency;damping ratio;overall modeling
TK83;TU279.7
A
国家自然科学基金资助项目(50638010)
2010-07-07 修改稿收到日期:2010-09-27
马人乐 男,教授,1951年生

