结构损伤识别的改进柔度灵敏度方法研究
杨秋伟,孙斌祥
(绍兴文理学院 土木工程系,绍兴 312000)
结构损伤识别的改进柔度灵敏度方法研究
杨秋伟,孙斌祥
(绍兴文理学院 土木工程系,绍兴 312000)
提出一种改进的柔度灵敏度方法用于工程结构损伤识别。通过在迭代算法中引入一个“加速”公式来迅速获得足够精确的识别结果,避免了多次迭代,可以大大减少计算花费。用两个数值算例对所提方法进行了验证,并把结果和原柔度灵敏度方法的计算结果进行比较。结果表明:采用改进的算法一般只需经过一次计算即可获得很高精度的识别结果,而采用原方法必须经过多次迭代才能获得相同精度的识别结果。改进的方法比原方法大大减少了迭代次数,显著减少了计算花费,显示了改进方法的突出优越性。
损伤识别;柔度灵敏度;“加速”公式
近年来,利用振动数据的改变来检测结构损伤的方法已引起土木、机械、航空和海洋等众多工程界的重视[1]。在已提出来的各类方法中,柔度方法有着较好的应用前景,因为柔度可由低阶的频率和振型便可以很精确的获得,且它比频率和振型对损伤更为敏感。Pandey 和 Biswas[2,3]利用结构柔度矩阵的改变来检测梁结构的损伤情况。Zhao和DeWolf[4]的研究表明结构柔度对损伤很敏感。Bernal[5]从柔度矩阵的改变量中分解出一系列的损伤定位向量来判断结构的损伤位置。Jaishi和Ren[6]根据模态柔度残余量来进行模型修正以识别结构损伤情况。Perara等[7,8]把柔度作为多目标函数之一,采用遗传算法来计算损伤参数。Yang[9]利用Neumann级数展开推导了结构柔度灵敏度的计算公式并提出了一种混合灵敏度方法,结合频率灵敏度和柔度灵敏度一起进行损伤识别。Yang和Liu[10]又研究了柔度改变量的特征值分解,据此提出一种判断损伤单元数目,确定损伤位置和求解损伤程度的新方法。
现有的关于柔度灵敏度方法的研究中均只考虑了柔度的一阶灵敏度,这对于小损伤的情况是适用的。对于结构发生大损伤的情况,则必须考虑二阶以上的灵敏度才能获得足够精确的计算结果,但这将显著增加计算花费。尤其是对于大规模的工程结构而言,过大的计算量是难以承受的。因此,一些学者使用迭代算法[11]来识别大损伤情况以减少计算量。然而,迭代算法的计算量仍然是比较大的,且随着损伤程度的增大,需要的迭代次数迅速增多,计算量将以几何级数增长。所以,寻求好的方法来进一步减少计算花费是很有意义的。本文基于这一点展开研究,提出一种改进的柔度灵敏度方法。通过在迭代算法的过程中引入一个加速公式来迅速获得足够精确的计算结果,避免了多次迭代。用两个数值算例对所提方法进行了验证。算例结果表明,无论损伤程度大小如何,采用本文方法,一般只需一次计算即可获得足够精确的识别结果,大大减少了计算量,显示了本文方法突出的优越性。
1 柔度灵敏度方法
本节对文献[9]中的柔度灵敏度方法作简单回顾,不失一般性,考虑一个n自由度的结构系统,假设只有第i个单元体损伤,则损伤后结构的刚度矩阵Kd为:

其中K是完好结构的刚度矩阵,αi和Ki是第i个单元体的损伤参数和刚度矩阵,K和Ki均为n×n维方阵。则损伤前后柔度改变量ΔF为:

方程(1)代入(2)可得:

方程(3)可用Neumann级数展开为:

忽略方程(4)中的高阶项,那么结构柔度的一阶灵敏度为:

其中F(F=K-1)是完好结构的柔度矩阵。由方程(5)可见,柔度灵敏度的计算是非常简单的因为它只需要完好结构的柔度矩阵F单元刚度矩阵Ki。根据线性叠加原理,若 N个单元体发生损伤,则 ΔF的一阶近似为:

另一方面,ΔF可以由损伤前后结构振动的前几阶模态获得:

其中m是测量的模态数目,F和Fd分别为损伤前后结构的柔度矩阵,λj和φj是未损伤结构的第j个特征值和振型,λdj和φdj为损伤结构的第 j个特征值和振型。由方程(6)和(7)可计算出未知的损伤参数αi(i=1~N),其方法是把矩阵方程(6)通过拉直运算转化为线性方程组,做法如下:

方程(8)中的上标横线“—”表示矩阵拉直,即将矩阵的各行元素按顺序排列形成一个列向量,即:
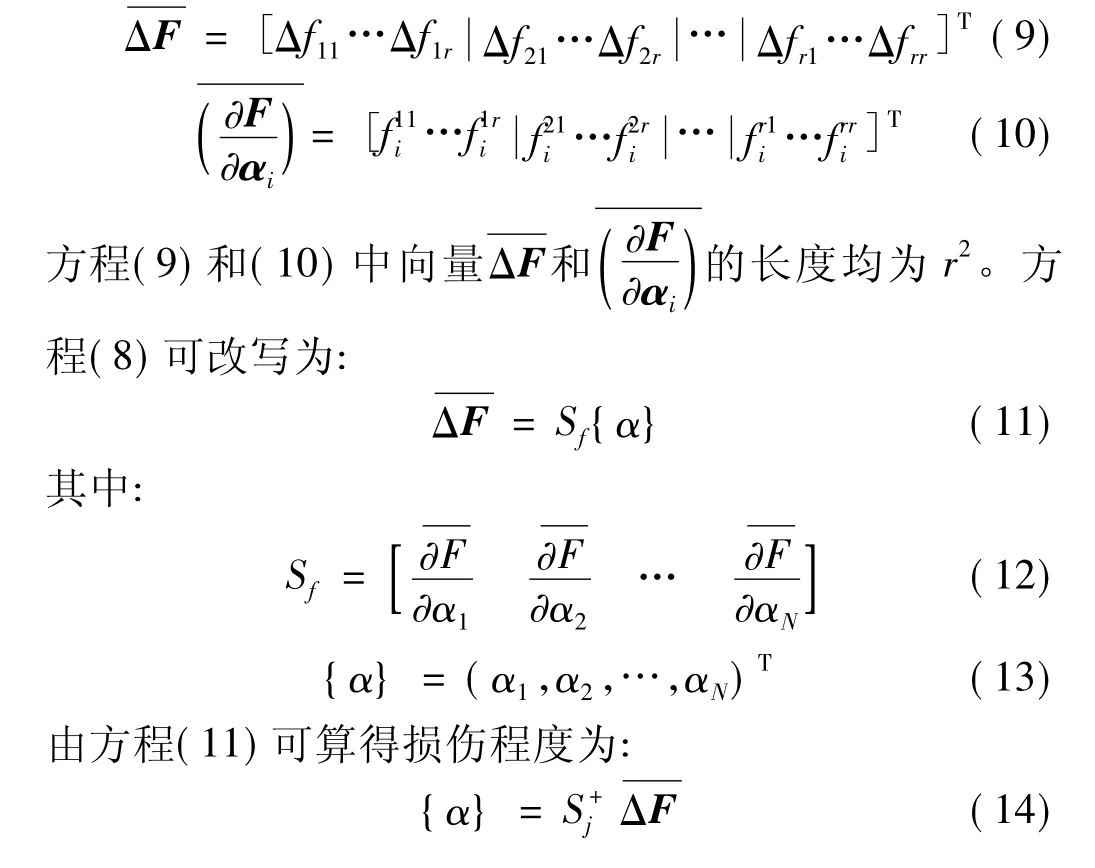
2 改进的柔度灵敏度方法
对于大损伤情况(一般指损伤程度超过15%时),由方程(14)计算所得的各单元损伤参数值{α}将和真实值存在很大的误差。造成误差的原因在于方程(4)中只考虑了一阶项,忽略了所有的高阶项。为了提高计算精度,可以采用迭代的算法,步骤如下:
(1)由方程(14)得到损伤参数第一次计算值{α},我们用{α}1来表示,上标“1”表示第一次计算。一般而言,如果{α}1中各元素α1i均不超过15%时,意味着这是小损伤情况,此时可不再进行后续的迭代步骤,{α}1可作为最终结果,由{α}1中各 α1i数值可以判定损伤单元位置和程度。但当{α}1中出现大于15%的参数时,意味着这是大损伤情况,应当进行后续的迭代计算以提高求解精度;
(2)更新结构总体刚度矩阵K,并把更新后矩阵作为新的“未损伤”刚度矩阵。为区别起见,我们用K1表示原未损伤刚度矩阵,用K2表示第一次更新后所得刚度矩阵,更新公式如下:


(3)再次使用方程(14)计算得到一组参数,这组参数我们称为相对损伤参数(因其是相对于步骤(2)中所假设的“未损伤”情况而言的),我们用{Δα}来表示,则经过第二次迭代计算后所得的各单元损伤程度计算值为:

考察{Δα},如果其中所有数值均小于某个规定的阀值(比如0.05),则迭代终止,所得{α}2即为最终计算结果,否则应转入第(2)步进行下一次迭代直至满足要求为止。
综上所述,迭代算法的计算量仍然是很大的,因为在步骤(2)中需要对新的刚度矩阵K2求逆,在步骤(3)中需要对新的柔度灵敏度矩阵求广义逆。因此,必须考虑新的方法来尽可能的减少迭代次数,降低计算量。本文提出如下的“加速”方法:
在每次由方程(14)计算得到损伤参数(或相对损伤参数)之后,对所得结果再进行一次“加速”运算,“加速”公式如下:

关于“加速”运算公式的数学依据推导如下:
根据单元刚度矩阵的特征值分解与组合,文献[10]中已证明:损伤前后结构的总体刚度矩阵K和Kd可以分解为(为了推导的方便,以单元刚度矩阵的秩等于1的结构为例,其它各类结构均可相应推导得出同样结论)

其中C=[c1,c2,…,cN],Ki=cicTi,C称为刚度联系矩阵(n×N维,且为满秩矩阵,n≤N)。Pd为对角矩阵,具体为:

结构的柔度矩阵和刚度矩阵互为逆矩阵,若矩阵C为方阵时(即n=N时,如本文算例1属于此类情况),由方程(18)和(19)可得结构损伤前后柔度矩阵为:
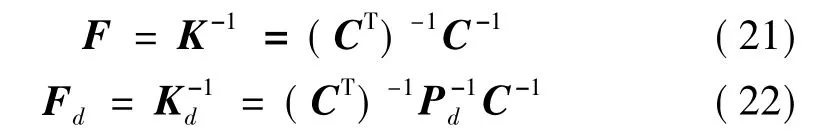
方程(22)减去(21)可得损伤前后柔度改变量为:
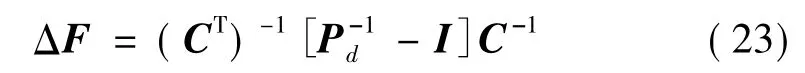
方程(23)中的矩阵I表示单位矩阵。容易证明以下两个等式成立:


将方程(24)和(25)代入(23)并展开可得:


对于矩阵C不为方阵的情况(即n<N时,如本文中的算例2属于此类情况),我们可以将以上推导中(方程(21)-(25))所用到的求逆运算(上标“-1”)均用广义逆运算(上标“+”)来近似代替,同样可以推导出方程(17)中的“加速”运算公式。
3 算例
采用两个数值算例来验证本文所提方法。算例1为一个3自由度弹簧-质量模型,算例2为一个二层的框架结构。算例1用于验证本文方法在完整且无误差模态数据下的识别结果,算例2用于验证本文方法在不完整且含误差数据下的识别结果。在每个算例中均讨论大损伤和小损伤两种情况。
3.1 算例1
以图1所示3自由度弹簧-质量系统为例验证本文方法在完整且无误差模态数据下的识别结果。未损伤时的物理参数为ki(i=1~3)和mj=1(j=1~3)。讨论3种损伤情况。情况1(单个小损伤情况):单元2刚度损伤15%;情况2:(单个大损伤情况):单元2刚度损伤80%;情况3:(多个大损伤情况):单元2和3刚度分别损伤60%和50%。3种情况下原柔度灵敏度方法和改进柔度灵敏度方法的第一次计算结果列于表1中。

图1 弹簧-质量系统(算例1)Fig.1 Spring-mass system for example 1

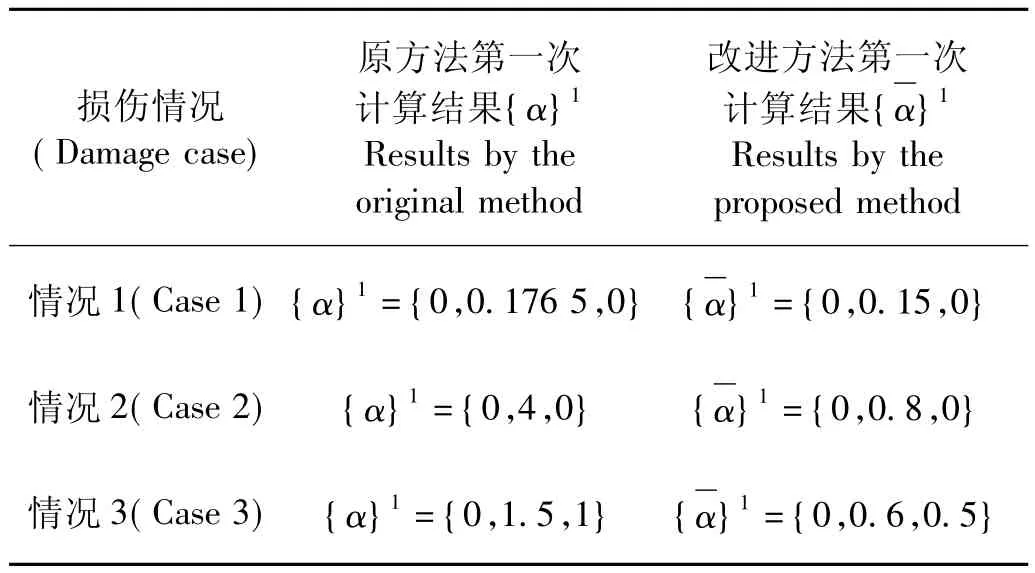
表1 两种方法第一次计算结果对比(算例1)Tab.1 Results of the first calculations by the two methods
3.2 算例2
以图2所示2层框架结构为例验证所提方法。该结构横截面为矩形(0.14 m×0.24 m),采用24个单元进行有限元分析,每单元长度为0.2 m,每个节点有3个自由度(水平和竖直2个平动自由度,1个转动自由度)。基本参数如下:横截面面积A=0.033 6 m2;惯性矩 I=1.612 8 ×10-4m4;弹性模量 E=200 GPa;剪切弹性模量 G=1.346 1 ×1010N/m2;泊松比 v=0.3;密度 ρ=2 500kg/m3。由于实践中的测量都是不完整的,故在本算例中我们只考虑前6阶模态,且结构中的柱只考虑其水平自由度而梁只考虑其竖直自由度,并且在每阶振型中加入5%的白噪声以模拟测量误差。


图2 二层的框架结构Fig.2 Two-storey frame structure

图3 单元6刚度损伤15%时两种方法第一次计算的结果Fig.3 Results of the first calculations by the two methods when element 6 is damaged with 15%stiffness loss
损伤情况2用两种方法第一次计算的结果见图4所示。由图4可见,两种方法均能准确识别出损伤位置,但原方法第一次计算得到的损伤程度和真实值相比误差很大,而改进方法仅经一次计算即可获得足够精确的结果。两种方法第一次计算所得的单元2和6的损伤参数值如下(括号内为误差):

上述结果显示了改进方法突出的优越性。对于结构发生大损伤的情况,采用改进的方法,仅需通过“加速”公式简单的四则运算,即可大幅度提高识别精度,不需要迭代只需经过一次计算即可获得足够精确的识别结果,大大降低了计算花费。而采用原方法若想获得相同精度的识别结果必须经过多次迭代方可,这将大大增加计算量。对于大规模的工程结构而言,由于其自由度成千上万,因迭代而增加的计算花费更是难以承受的,所以本文所提的改进方法更加有着突出的价值。

图4 单元2和6刚度均损伤50%时两种方法第一次计算的结果Fig.4 Results of the first calculations by the two methods when elements 2 and 6 are damaged with 50%stiffness loss
4 结论
现有的灵敏度方法一般只考虑了一阶灵敏度,这对于结构发生小损伤情况是适用的,利用一阶灵敏度分析即可获得较好的识别结果。但对于结构发生大损伤的情况,则必须考虑高阶灵敏度或者采用迭代的算法才能获得足够精确的计算结果,但这要大量增加计算花费。为了显著降低计算花费,本文提出一种改进的柔度灵敏度方法,通过在迭代算法的过程中引入一个简单的“加速”公式,便能迅速获得良好精度的识别结果。以两个数值算例验证了所提的方法。算例结果表明:无论结构损伤程度如何,用本文所提的改进方法一般只需经过一次计算即可获得很好的识别结果。对于结构发生小损伤的情况,改进方法比原方法计算结果精度明显提高;对于结构发生大损伤的情况,原方法第一次计算结果的误差非常大,必须经过多次迭代才能获得满意的识别结果,而改进方法仅经过一次计算即可获得足够精度的识别结果,显示了改进方法突出的优越性。
[1]杨秋伟.基于振动的结构损伤识别方法研究进展[J].振动与冲击,2007,26(10):86-91.
[2]Pandey A K,Biswas M.Damage detection in structures using changes in flexibility[J].Journal of Sound and Vibration,1994,169:3-17.
[3]Pandey A K, BiswasM. Experimentalverification of flexibility difference method for locating damage in structures[J].Journal of Sound and Vibration,1995,184(2):311-328.
[4] Zhao J, DeWolfJ T. Sensitivity study forvibrational parameters used in damage detection [J]. Journalof Structural Engineering,ASCE,1999,125(4):410-416.
[5]Bernal D.Load vectors for damage localization[J].Journal of Engineering Mechanics,2002,128(1):7-14.
[6]Jaishi B,Ren W X.Damage detection by finite element model updating using modal flexibility residual[J].Journal of Sound and Vibration,2006,290:369-387.
[7]Perera R, Ruiz A, Manzano C. An evolutionary multiobjective framework for structural damage localization and quantification [J].Engineering Structures,2007,29:2540-2550.
[8]Perera R,Ruiz A.A multistage FE updating procedure for damage identification in large-scalestructuresbased on multiobjective evolutionary optimization [J].Mechanical Systems and Signal Processing,2008,22(4):970-991.
[9]Yang Q W.A mixed sensitivity method for structural damage detection[J].Communications in Numerical Methods in Engineering,2009,25(4):381-389.
[10] Yang Q W, LiuJK. Damageidentification bythe eigenparameter decomposition of structural flexibility change[J]. InternationalJournalforNumericalMethods in Engineering,2009,78(4):444-459.
[11]Shi Z Y ,Law S S,Zhang L M.Damage localization by directly using incomplete mode shapes.Journal of Engineering Mechanics,2000,126(6):656 -660.
[12] Wang X,et al.Structural damage identification using static test data and changes in frequencies[J].Engineering Structures,2001,23:610 -621.
[13] Bakhtiari-Nejad F,Rahai A,Esfandiari A.A structural damage detection method using static noisy data[J].Engineering Structures,2005,27:1784-1793.
An improved flexibility sensitivity method for structural damage detection
YANG Qiu-wei,SUN Bin-xiang
(Department of Civil Engineering,Shaoxing University,Shaoxing 312000,China)
Structural damage identification based on an improved sensitivity technique of structural flexibility was studied here.The drawback of the existing sensitivity methods was discussed firstly and then an improved technique was presented.The significant contribution of this study was to induce a simple accelerating formula in to iteration processes.With the introduction of the accelerating formula,the proposed method was able to identify damages without any high-order analysis of flexibility or multi-iteration.The effectiveness of the proposed method was illustrated using simulated data with measurement noise of two numerical examples.The results showed that the proposed procedure is economical for computation and simple to implement;regardless of damages being small or large,the proposed method can identify both locations and levels of structural damages accurately only using one iteration;the presented scheme may be useful for structural damage identification.
damage detection;flexibility sensitivity;accelerating formula
O32;TH113.1
A
浙江省自然科学基金项目(Y1110949);绍兴市科技计划重点项目(2010A23006);国家自然科学基金项目(40772194)
2010-01-11 修改稿收到日期:2010-03-31
杨秋伟 男,博士,副教授,1979年9月生

