不变本征算符法计算各向异性Heisenberg反铁磁系统的自旋波能量

成泰民， 葛崇员， 李青云， 孙树生

(沈阳化工大学数理系，辽宁沈阳110142)

范洪义的论文［1-2］较详细地介绍了不变本征算符法应用.因为体系的任意幺正变换联系着同一个量子体系的不同表象之间的变换，所以，蕴含着该量子体系的严格一致的物理内容，这些幺正变换对该量子体系的描述是完全等价的.因此，在磁性物理及量子力学中普遍采用不同的幺正变换处理系统哈密顿量的对角化，求出元激发能量及基态能量.但是这一方法的关键是做出适合体系对角化的不同的幺正变换，利用幺正变换处理体系哈密顿量的过程也比较繁琐［3-4］.封闭链的格林函数的运动方程法［5］(切断近似法)也能够处理体系元激发能量，利用此方法处理体系哈密顿量的过程中，关键是算符与哈密顿量之间的对易律，在此可以少考虑文献［3-4］中的部分幺正变换(如Bogoliubov变换［3-4］等(注:文献［3］与［4］的Bogoliubov变换表示形式不同，但都是幺正变换.只是文献［3］中的Bogoliubov变换表示更凸显其幺正性.)).本文用不变本征算符法处理线性近似下的Hamiltonian量体系的元激发能量，比上述两种方法简捷.

1 不变本征算符法［1-2］

或者

假设{|ψa〉，|ψb〉，…}是系统哈密顿量 ^H的本征态集合，构成希尔伯特空间的完备态矢量集，且对应的本征值为{Ea，Eb，…}.由(1)式、(2)式可得:

根据(3)式、(4)式可得:

从而可知，利用IEO方法无须涉及系统的具体量子态及波函数，可以直接对算符进行操作得出系统的能谱.IEO方法的关键是做出所研究系统的不变本征算符，这一方法极大地简化了系统能谱的求解过程.但是IEO方法所计算的λ对应的不是系统的能级，而是能级差.

2 各向异性Heisenberg反铁磁系统

设单位体积内总格点数为2N，可分为A、B两个子晶格.X-Y-Z模型各向异性Heisenberg反铁磁系统的Hamiltonian量表示为:

把(8)式、(9)式代入到(7)式，只保留到算符的二次项就可得线性近似下的哈密顿量，再进行(10)式的宇称变换，并考虑哈密顿量的厄米性可得:

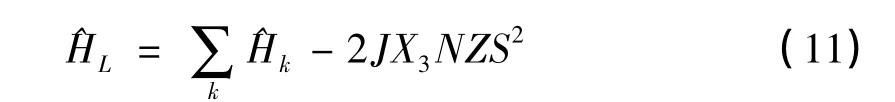
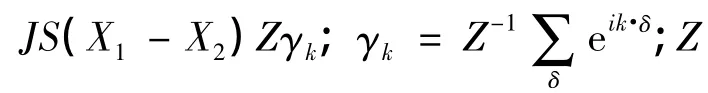
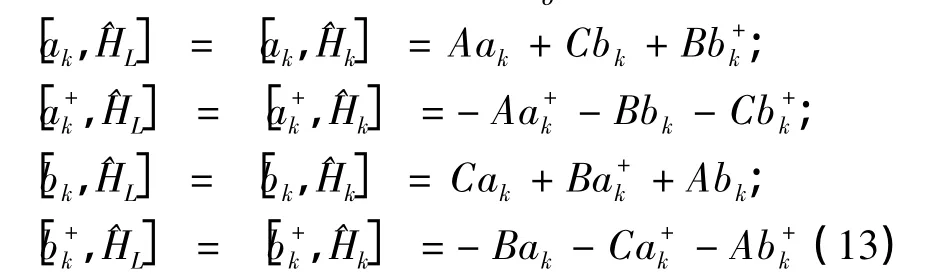
根据(13)～(15)式，可得:

从而得:

由(17)式得到非平庸解的条件为系数行列式等于零.从而可得:

在(18)式中，舍负取正并把(12)式中的系数代入到(18)式，可得X-Y-Z模型各向异性Heisenberg反铁磁系统的自旋波能量:

(19)式与文献［4］的结果一致(注:因在本文中令单位体积内总格点数为2N，所以，与文献［4］系数上相差2倍.这是因为在文献［4］中令单位体积内总格点数为 N之故).(19)式中“+”对应光学支自旋波能量，“-”对应声学支自旋波能量.这与不同的幺正变换方法［3］所得到的结果完全一致.单从二粒子耦合体系［3］的元激发能量而言，这一结果与封闭链的格林函数运动方程法［5］计算的结果也一致，并且处理方法较相似，但是IEO方法更简捷.

3 讨论

(1)由(19)式，当X1=X2=X，X3=1时，可得X-Y-Z模型Heisenberg反铁磁系统的自旋波能量如下:

由(20)式，当 X=1时，可得各向同性Heisenberg反铁磁系统的自旋波能量=2JZS与文献［6-7］一致.由此可知对称性越高(有序度降低)，系统越易出现简并现象［8］.这也与可观测程度相关，系统具有某种对称性，意味着存在某一物理量是不可观测量.如果这种对称性破缺了，那么这一物理量就成为可观测量.在此对称性破缺与X1≠X2相关，当X1=X2时，由(20)式可知，Heisenberg反铁磁系统的自旋波能量出现简并现象.

(2)利用IEO方法计算磁有序系统的自旋波能量非常方便，但是IEO方法不易给出磁有序系统的基态能量，并且利用IEO方法几乎无法处理含有算符的三次项或者更高次项的Hamiltonian量体系(如电子-声子耦合体系，磁振子-声子耦合体系，声子-声子耦合体系，磁振子-磁振子耦合体系等)，在这一点IEO方法不如格林函数理论及量子场论的费曼图技术.这是因为IEO方法计算的结果是能级差，对应的是磁有序系统的元激发能量;而且处理含有算符的三次项或者更高次项的Hamiltonian量体系时，涉及到算符与Hamiltonian量对易关系变得越来越复杂，并存在算符的幂次增大趋势，对应Hamiltonian量的IEO又不易做出.因为线性近似下的Hamiltonian量只包含算符的二次项，所以，利用IEO方法及算符的对易关系，能够简捷地计算出线性近似下的Hamiltonian量体系的元激发能量.

［1］ Fan HongYi，Li Chao.Invariant‘Eigen-operator’of the Square of Schrödinger Operator for Deriving Energy-level Gap［J］.Phys.Lett.A，2004，321:75-78.

［2］ Fan HongYi，Wu Hao.Deriving Vibrating Modes of Some Multiatom Molecules by Virtue of the Invariant Eigenoperator Method［J］.Modern Physics Letters B，2005，19(26):1361-1366.

［3］ 柳盛典，逯怀新，邓汝刚.幺正变换与二粒子耦合体系哈密顿量的对角化技术［J］.大学物理，1993，12(5):25-26.

［4］ 何兵，应和平，季达人.X-Y-Z非各向同性反铁磁Heisenberg系统的自旋波解［J］.物理学报，1996，45(3):522-527.

［5］ 蔡建华，龚昌德，姚希贤，等.量子统计的格林函数理论［M］.北京:科学出版社，1982:195-227.

［6］ 戴道生，钱昆明.铁磁学(上册)［M］.北京:科学出版社，1987:270-276，283，288.

［7］ 李正中.固体理论［M］.北京:高等教育出版社，2002:68-70，80，84.

［8］ 于禄，郝柏林，陈晓东.边缘奇迹:相变和临界现象［M］.北京:科学出版社，2005:36-47，87-92.