椭圆环形刚体转动惯量的数值计算

于志明

(连云港师范高等专科学校物理系 江苏 连云港 222006)

文献[1]讨论了椭圆环形刚体的转动惯量，结果用椭圆积分给出，使用时要查《椭圆积分表》，很不方便.我们用Matlab编程对椭圆环形刚体的转动惯量进行了数值计算和多项式拟合，可以快速计算出椭圆环形刚体的转动惯量.

1 椭圆环形刚体的转动惯量

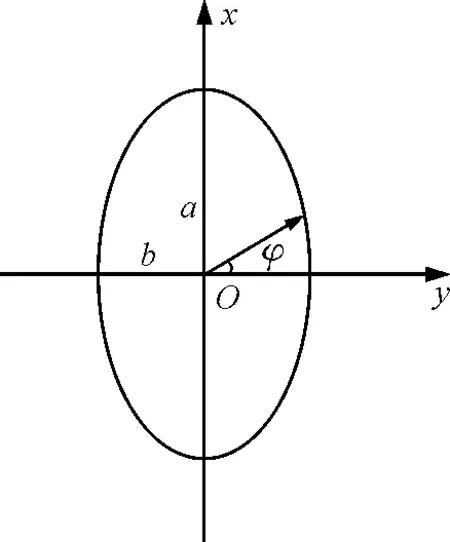
图1

如图1所示，一质量为m，半长轴为a，半短轴为b的均质椭圆环形刚体，其解析方程可表示为

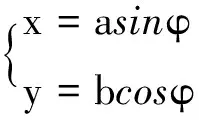
(1)

其周长为

(2)

该椭圆环形刚体对过环中心且与环面垂直的轴线的转动惯量可表示为

I=

(3)

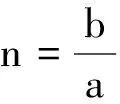
(4)

则式(3)变为

I=

(5)

令I(n)=

(6)

则式(5)变为

I=ma2I(n)

(7)

由式(6)定义的I(n)只与n有关，也即只与椭圆的具体形状有关.由式(7)可知，只要计算出I(n)，就计算出了椭圆环形刚体的转动惯量.但I(n)的分子、分母是两个比较难的积分.根据文献[1]，可以将I(n)用椭圆积分来表示，结果为

(8)

式(8)中的F(k)为

(9)

为第一类全椭圆积分.式(8)中的E(k)为

(10)

为第二类全椭圆积分.式(8)、(9)、(10)中的k为椭圆的偏心率，k与n的关系为

(11)

式(8)具体的积分结果要根据k值查椭圆积分表，这显然很不方便.因而，我们设法对I(n)作数值计算，进而实现对椭圆环形刚体转动惯量的数值计算.

2 椭圆环形刚体转动惯量的数值计算

根据文献[2]，利用Matlab的数值积分指令编程，先对I(n)的分子、分母中的两个积分进行数值计算，进而算得I(n).具体程序为

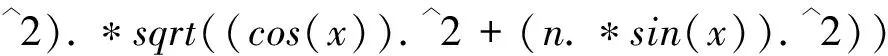
＇x＇,＇n＇);

s1=quad(y1,0,pi/2,[],[],n);

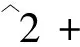
s2=quad(y2,0,pi/2,[],[],n);

I=s1/s2

取定n,将其填入第2,4句中，就可以得到相应的I(n).

如当n=0时，I(n)=0.333 3；

当n=0.215时，I(n)=0.391 7；

当n=1时，I(n)=1；

当n=5.1时，I(n)=9.967 9；

当n=11.5时，I(n)=45.6787；

……

这比通过查椭圆积分表求I(n)方便多了.

如在上边的程序中加上循环语句，就可以一次连续计算出很多与n相应的I(n)，进而可以画出I(n)与n的关系曲线，从中可以看出I(n)随n的变化规律.图2给出了n在0～20之间取值时I(n)随n变化的情况.

图2

由对I(n)数值计算的结果，利用Matlab中的多项式拟合指令，还得到了I(n)的多项式表达式，结果为

I(n)=0.000 4n3+0.315 9n2+0.246 1n+0.333 3

(12)

因此，椭圆环形刚体的转动惯量可表示为

(13)

将椭圆环形刚体的质量m,半长轴a,半短轴b的值代入式(13)，可以计算出该椭圆环形刚体的转动惯量.

参考文献

1 赵新闻,周欣然,杨兵初.椭圆环形刚体的转动惯量.大学物理,2008,27(6):13～14

2 彭芳麟,管靖,胡静,卢圣治.理论力学计算机模拟.北京:清华大学出版社,2002.66～69