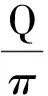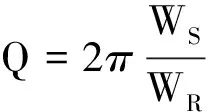串联谐振电路Q值的计算与意义
杨晓雷
(上海师范大学数理学院 上海 200234)
在实际电路中,即使是一个简单的线圈,不仅有电感,还有电阻,不能分割,但可以用集中的电感L与电阻R串联电路模型来表示.作为具有代表性的典型模型,经常研究电阻、电感、电容串联电路.
1 RLC串联电路的特点与谐振现象
如图1所示是由电阻、电感和电容相串联所组成的RLC串联电路.在此电路中,电容和电感是储能元件,其中能量的转换是可逆的,而电阻是耗能元件,其中电能单向地转为热.
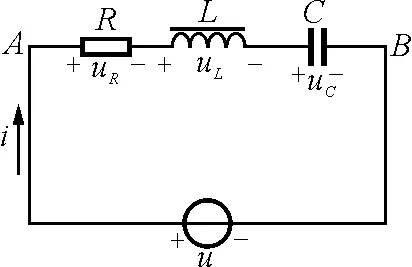
图1 RLC串联电路
由电阻R,电感L,电容C与直流电源组成的各种组合电路中,当电源由一个电平的稳定状态变为另一个不同电平的稳定状态时(如接通或断开直流电源),由于电路中电容上的电压不会瞬间突变和电感中的电流不会瞬间突变,这样电路由一个稳定状态变到另一个稳定状态中间要经历一个变化过程,这个变化过程称为暂态过程.利用暂态过程的规律可以测量R,L,C元件的量值,也可用于产生脉冲信号(如锯齿波、微分脉冲信号等).而RLC串联电路如果与频率可调的交流电源组合后,当电源的频率与RLC串联电路的固有频率相等时,会发生谐振现象.因而暂态过程的规律和谐振现象在电磁学、电子技术等领域中的用途非常广泛.
1.1 RLC串联电路的特点
从能量变化的角度来说明,由于RLC串联电路中存在着两种不同性质的贮能元件,因此它的过渡过程就不仅是简单的积累能量和释放能量,还可能发生电容的电场能量和电感的磁场能量相互反复交换的过程,这一点决定于电路参数.当电阻比较小时(该电阻应该是电感线圈本身的电阻和回路中其余部分电阻之和),电阻上消耗的能量较小,而L和C之间的能量交换占主导位置,所以电路中的电流表现为振荡过程.当电阻较大时,能量来不及交换就在电阻中消耗掉了,使电路只发生单纯的积累或释放能量的过程,即非振荡过程.
在RLC串联电路中,无论电压、电流怎样变化,在任意时刻,它们仍应该遵守基尔霍夫定律.
1.1.1 电压与电流的瞬时关系
设在上述电路中通过的正弦交流电流为i=Imsinωt,则
uR=ImRsinωt
u=uR+uL+uC
1.1.2 相量图(图2,以电流为参考相量)

图2 电流与电压关系的相量图
1.1.3 端电压与电流的关系
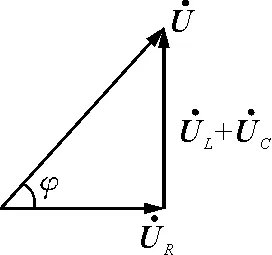
图3 电压三角形
(1)大小关系
1)电压三角形:电路的端电压与各分电压构成一直角三角形,叫电压三角形(图3).
2)RLC串联电路中欧姆定律的表达式
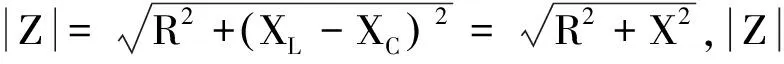
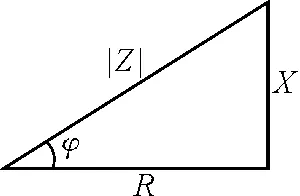
图4 阻抗三角形
3)电抗:感抗与容抗之差叫做电抗.用X表示X=XL-XC,单位为Ω.
4)阻抗三角形:如图4所示,阻抗角φ为|Z|与R两个边的夹角
(2)相位关系
1)当XL>XC时,端电压超前电流φ角,电路呈电感性,称为电感性电路.
2)当XL 3)当XL=XC时,端电压与电流同相,电路呈电阻性,电路的这种状态叫串联谐振. 在RLC串联电路中,当电路端电压和电流同相时,电路呈电阻性,电路的这种状态叫串联谐振.谐振是正弦交流电路在特定条件下产生的一种特殊物理现象.谐振现象在无线电和电工技术中得到广泛应用,研究电路中的谐振现象有重要的实际意义.交流电路的谐振有很多用途,一般可用于测量电感、电容、频率,还可用于选频、陷波、调谐放大、作振荡器和频率补偿等. 1.2.1 串联谐振的条件 由以上分析可知,串联电路发生谐振的条件是 XL-XC=0 或XL=XC 即 1.2.2 实现电路谐振的方法 (1)如果电感L和电容C固定不变,可通过改变电源频率使电路谐振.设串联谐振时的角频率为ω0,频率为f0,则 其中L的单位为H,C的单位为F,f0的单位为Hz. 谐振时的角频率和频率仅决定于电路的电感和电容的量值,是电路所固有的.所以f0和ω0常称为电路的固有频率和电路的固有角频率.当电源频率等于电路的固有频率时,电路发生谐振. (2)如果电源的频率一定,可改变电感或电容使电路谐振. 改变电感或电容,都能改变电路的固有频率f0,使f0等于电源频率f,电路就出现谐振现象.调节L或C使电路谐振的过程称为调谐. 1.2.3RLC串联谐振的基本特点 (2)谐振时,电路中电流最大,且与电源电压同相. (3)谐振时,电路的电抗为零,感抗和容抗相等并等于电路的特性阻抗ρ. 由于谐振时 则 所以 (4)谐振时,电感与电容两端的电压相等,且相位相反,其大小为电源电压U的Q倍. 则 UL0=UC0=QU 电路的Q值一般在50~200之间.因此,即使外加电源电压不高,在谐振时,电路元件上的电压仍然可能很高,特别对于电力电路来说,这就必须注意到元件的耐压问题和设法避免过电压问题. 1.2.4RLC串联电路谐振时的功率关系 有功功率 电源向电路输送电阻消耗的功率,电阻功率达到最大. 无功功率 Q=UIsinφ=QL+QC=0 稳态时,电源不向电路输送无功功率.电感中的无功功率与电容中的无功功率大小相等,互相补偿,彼此进行能量交换. 1.2.5RLC串联电路谐振时的能量关系 在RLC串联电路中,电阻是耗能元件,它把电、磁能转换成热;电容和电感是储能元件,它们时而储存电、磁能,时而放出,彼此交换能量,而不消耗. 在交流电的一个周期T里,电阻元件中消耗的能量为 WR=RI2T 电容两端的电压 电容的储能 电感的储能 电路的总储能 上式表明,电感和电容的能量按余弦或正弦规律变化,最大值相等,即WLm=WCm.L,C的磁场能量和电场能量作周期性地交换,而不与电源进行能量交换.在一般的情况下,WS是随时间做周期变化的量,这表明,谐振电路与外界交换无功功率.但是在谐振状态下 这时WS不再随时间变化,且等于最大值,亦即谐振电路不再与外界交换无功功率.WS=LI2就是在谐振状态下稳定地储存在电路中的电、磁能,这能量是在谐振电路开始接通时经历的暂态过程中由外电路输入给它的.达到稳定的振荡以后,为了维持振荡,外电路需不断地输入有功功率,以补偿上述WR的损失,但在谐振状态下无需再供给无功功率. 在谐振时,一般Q≫1,UR=U,UL0=UC0=QU≫U,即电感和电容的电压相等,并且是信号源电压的Q倍(几十到几百倍),故串联谐振电路又称为电压谐振电路.串联谐振电路的这个特点为我们提供了测量电抗元件Q值的一种方法.最常用的一种测Q值的仪器——Q表,就是利用上述原理制成的.例如,当一个谐振电路Q值为100时,若电路两端加6 V的电压,谐振时电容或电感上的电压将达到600 V,在实际操作中不注意到这一点,就会很危险.电力系统中,常常尽量避免谐振,以免击穿电路设备(L,C等);而电子线路中,常用此方法获得高压. 图5 Z,I,φ随频率的变化曲线 电流谐振曲线表明,由于串联谐振回路的谐振特性,使它对ω0附近的频率产生很大的电流,对远离ω0的频率产生的电流却很小,这表明串联谐振回路对不同频率的信号有不同的响应,这种响应说明串联谐振回路具有选择所需频率信号的能力,即能把ω0附近的无线电信号选择出来,同时也能把远离ω0的频率成分加以削弱和抑制.所以串联谐振回路可以用作选频电路. 回路中电流的有效值为 即 图6 串联谐振回路的电流幅频特性曲线 从图6上可以清楚地看到,较大的Q值对应着较尖锐的电流谐振曲线,而较尖锐的电流谐振曲线意味着有较高的回路选择性.所以回路的Q值愈大,回路的选择性就愈高. 在电子技术中,回路的Q值一般是Q≥1,因而电流谐振曲线比较尖锐.当信号频率ω远离ω0时,回路电流已经很小了.这就是说,远离ω0的信号对电路的影响基本上可以忽略不计.所以只考虑信号频率ω接近ω0时的情况,在这种情况下可以认为 ω+ω0≈2ω 有 则 图7 串联谐振回路谐振曲线的通频带 B=f2-f1=(f2-f0)+(f0-f1)≈ Δf+Δf=2Δf 只要选择回路的通频带大于或等于信号的频带,使信号频带落在回路的上、下边界f2和f1之内,信号通过回路后产生的幅度失真是允许的. 由通频带的定义可知,在通频带的边界频率上有 令 则 因而得 即谐振电路的通频带宽度Δf反比于谐振电路的Q值,Q值越大(即损耗越小),谐振电路的选择性越强.由此得出结论(图6): (1)Q值越高,幅频特性曲线越尖锐,电路对偏离谐振频率的信号的抑制能力越强,电路的选择性越好. (2)Q值越高,电路的带宽越窄. (3)谐振电路的实际应用举例——收音机选台 为减小信号失真,要求带宽尽可能宽,希望Q值小;为抑制临近电台信号干扰,要求选择性要好,希望Q值大. 实际设计时,要选取适当的Q值,以兼顾选择性和带宽的要求. 前面所提到的RLC串联电路的暂态过程与谐振问题有着密切的联系,因为研究的对象是共同的,即RLC串联电路,区别只在于电路中一个无源,一个有源.在R很小时,无源RLC串联电路能按照自身的固有频率或周期振荡,其固有频率 周期 它在频率为ω的交流电源作用下受迫振荡时,就会在ω=ω0的条件下发生谐振,这也是振动现象的普遍规律.既然Q值是这个电路本身的性质,可以料到,它不仅在谐振现象中多方面表现出来,在暂态过程中也会有一定的表现. 即 故 其实,第四种意义与前面所说的第一种意义(Q值等于谐振电路中储存的能量与每个周期内消耗能量之比的2π倍)有着密切的联系.在每个周期T内 参考文献 1 冯杰.大学物理专题研究.北京:北京大学出版社,2010 2 赵凯华,陈熙谋.电磁学.北京:高等教育出版社,2006 3 梁灿彬,等.电磁学.北京:高等教育出版社,2004 4 邱关源.电路.北京:高等教育出版社,2006 5 李树燕.电路基础.北京:高等教育出版社,1994 6 周绍敏.电工基础.北京:高等教育出版社,20061.2 RLC串联电路的谐振
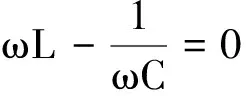

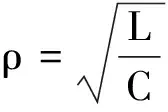
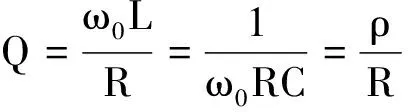
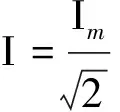

2 RLC串联谐振电路Q值的意义
2.1 Q值的第一种意义——储能与耗能
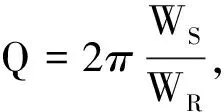
2.2 Q值的第二种意义——电压分配
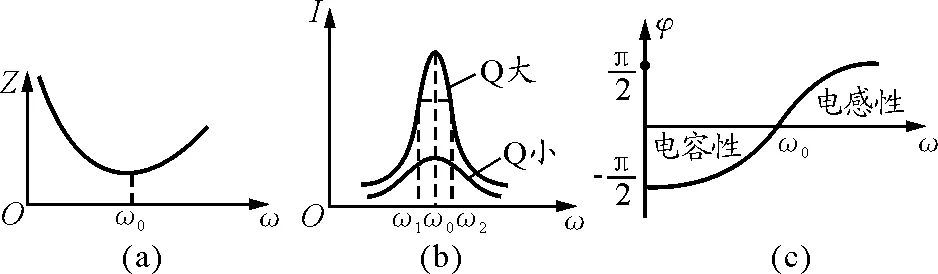
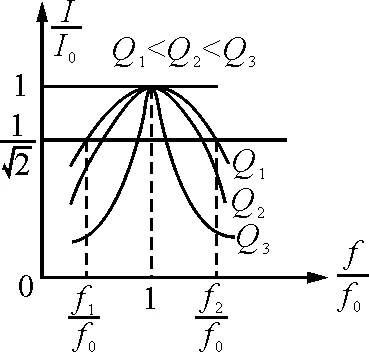
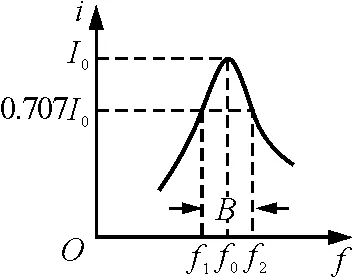
2.3 Q值的第三种意义——频率的选择性
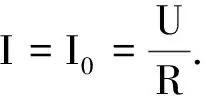
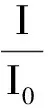
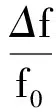
2.4 Q值的第四种意义——阻尼振荡