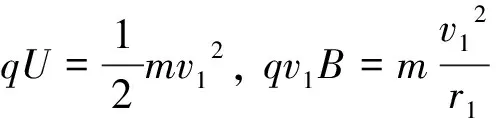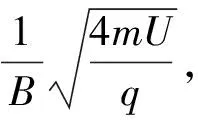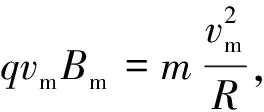圆形有界磁场问题的分类及解析
周平原
(临海市回浦中学 浙江 台州 317000)
1 对心飞入问题
【例1】(2002年高考天津卷)电视机的显像管中,电子束的偏转是用磁偏转技术实现的.电子束经过电压为U的加速电场后,进入一圆形匀强磁场区,如图1所示.磁场方向垂直于圆面.磁场区的中心为O,半径为r.当不加磁场时,电子束将通过O点而打到屏幕的中心M点.为了让电子束射到屏幕边缘,需要加磁场,使电子束偏转一已知角度θ,此时磁场的磁感应强度B应为多少?
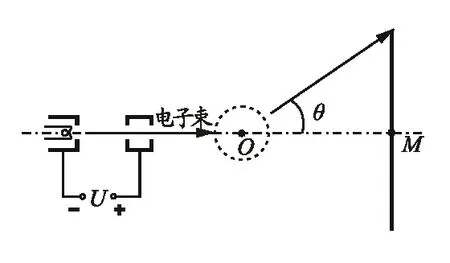
图1
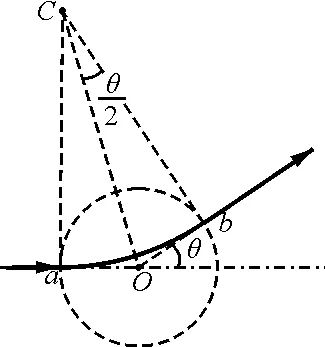
图2
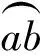
又有
三式联立解得
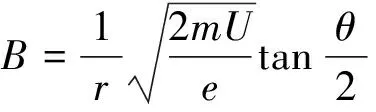
点评:粒子沿半径方向飞入圆形匀强磁场,必沿半径方向飞出磁场.
2 圆心出发问题
【例2】(2004年高考甘肃卷) 一匀强磁场,磁场方向垂直于xOy平面,在xOy平面上,磁场分布在以O点为中心的一个圆形区域内.一个质量为m、电荷量为q的带电粒子,由原点O开始运动,初速度为v,方向沿x轴正方向.后来粒子经过y轴上的P点,此时速度方向与y轴的夹角为30°,P到O的距离为L,如图3所示.不计重力的影响.求磁场的磁感应强度B的大小和xy平面上磁场区域的半径R.
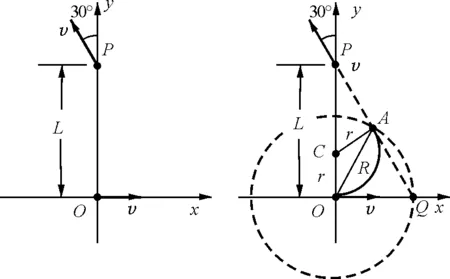
图3 图4
解析:如图4所示,粒子在磁场中轨迹的圆心C必在y轴上,且P点在磁场区之外.粒子从A点离开磁场区,设轨迹半径为r.则
又
可求得
磁场区域的半径
点评:画轨迹时可先画一个完整的圆,然后分析粒子从圆周上哪一点离开,速度方向才会与题意相符,只要找到了离场点,问题就能解决了.
3 最长时间(最大偏角)问题

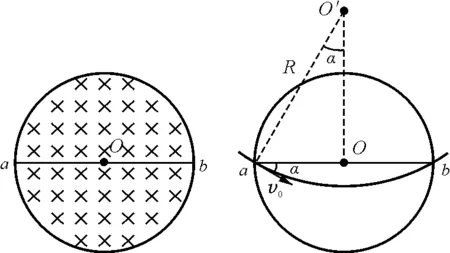
图5 图6
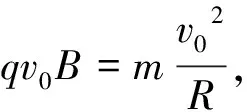
要使粒子在磁场中运动的时间最长,应使粒子在磁场中运动的圆弧最长,即所对应的弦最长.则以磁场圆直径ab为弦时,粒子运动的时间最长.
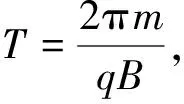

点评:粒子穿过圆形磁场时,以磁场圆直径ab为弦时,粒子运动时间最长,偏转角最大.
4 最小半径问题
【例4】(1994年高考全国卷) 如图7所示,一带电质点,质量为m,电荷量为q,以平行于x轴的速度v从y轴上的a点射入图中第一象限所示的区域.为了使该质点能从x轴上的b点以垂直于x轴的速度v射出,可在适当的地方加一个垂直于xy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,试求这圆形磁场区域的最小半径.重力忽略不计.


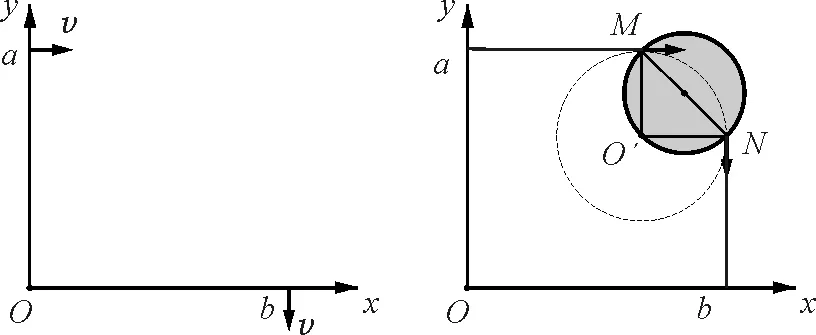
图7 图8
点评:粒子穿过圆形磁场时,若轨迹是确定的,则以轨迹圆弧对应的弦为直径时,磁场圆最小.
5 会聚一点问题
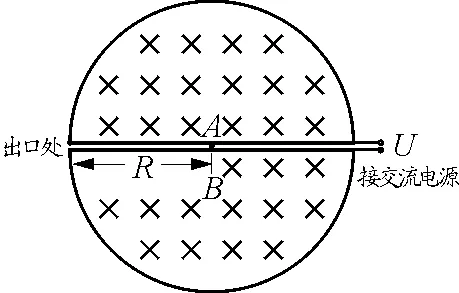
【例5】(2009年高考浙江卷) 如图9所示,x轴正方向水平向右,y轴正方向竖直向上.在xOy平面内有与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场.在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m,电荷量q(q>0)和初速度v的带电微粒.发射时,这束带电微粒分布在0 (1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域,并从坐标原点O沿y轴负方向离开,求电场强度和磁感应强度的大小和方向. (2)请指出这束带电微粒与x轴相交的区域,并说明理由. (3)若这束带电微粒初速度变为2v,那么它们与x轴相交的区域又在哪里?并说明理由. 图9 图10 带电微粒进入磁场后,做圆周运动并从坐标原点O沿y轴负方向离开,则轨迹半径r=R (2)如图10所示,从任一点P水平进入磁场的带电微粒在磁场中做半径为R的匀速圆周运动,圆心位于其正下方的Q点,微粒从M点离开磁场.可证明四边形PO'MQ是菱形,则M点就是坐标原点,故这束带电微粒都通过坐标原点O. (3)带电微粒在y轴右方(x>0)的区域离开磁场并做匀速直线运动.靠近上端发射出来的带电微粒在穿出磁场后会射向x轴正方向的无穷远处,靠近下端发射出来的带电微粒会在靠近原点之处穿出磁场.所以,这束带电微粒与x轴相交的区域范围是x>0. 点评:一束带电粒子以平行的初速度v垂直射入圆形匀强磁场,若带电粒子的轨道半径与磁场圆半径相同,则这些带电粒子将会聚于初速度方向与磁场圆的切点. 【例6】 电子质量为m,电荷量为e,从坐标原点O处沿xOy平面射入第一象限,射入时速度方向不同,速度大小均为v0,如图11所示.现在某一区域加方向向外且垂直于xOy平面的匀强磁场,磁感应强度为B,若这些电子穿过磁场后都能垂直射到荧光屏MN上,荧光屏与y轴平行,求荧光屏上光斑的长度. 图11 图12 点评:速度大小相等的一束带电粒子从圆周上同一点沿不同方向垂直射入圆形匀强磁场,若粒子的轨道半径与磁场圆半径相同,那么所有粒子成平行线离开磁场,而且与磁场圆在入射点的切线方向平行. 【例7】(2009年高考海南卷)如图13所示,ABCD是边长为a的正方形.质量为m,电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC边射入正方形区域.在正方形内适当区域中有匀强磁场.电子从BC边上的任意点入射,都只能从A点射出磁场.不计重力,求: (1)此匀强磁场区域中磁感应强度的方向和大小; (2)此匀强磁场区域的最小面积. 图13 图14 解析:(1)让平行粒子束射入圆形匀强磁场,若轨道半径与磁场圆半径a相同,则这些带电粒子将会聚于初速度方向与磁场圆的切点A. 点评:此题也属会聚一点问题,圆形磁场内刚好能覆盖粒子轨迹范围的部分,就是所要求的磁场最小面积. 【例8】某平面内有M,N两点,距离为L,从M点向此平面内各个方向发射速率均为v的电子,请设计一种匀强磁场分布,使得由M点发出的电子都能汇聚到N点.要求画出匀强磁场分布图,并加以必要的说明,电子质量为m,电荷量为e. 图15 点评:此题是平行离开和会聚一点问题的综合,需要较好的空间想象能力. 【例9】如图16所示,半径为R的圆筒形区域内,分布着磁感应强度为B,方向垂直纸面向里的匀强磁场,一带正电的微粒从圆筒壁上小孔A点沿半径方向射入磁场,且初速度方向垂直于磁场方向.若该微粒与筒壁碰撞时不损失电荷量,并能以大小相等的速度反向弹回,问初速度大小满足什么条件时,微粒能回到A点,并求出微粒回到A点所经历的时间.已知微粒质量为m,电荷量为q,不计微粒重力. 图16 图17 点评:由于微粒轨迹有无数种可能,关键是理清几何关系找到通式. 图18 (1)粒子沿环状半径方向射入磁场,不能穿越磁场的最大速度; (2)所有粒子不能穿越磁场的最大速度. 图19 点评:应分析粒子的可能轨迹,从中找到刚好不出磁场的临界轨迹. 图20 图21 点评:分析粒子的入场点和出场点从而确定轨迹是关键. 【例12】(2009年高考江苏卷)1932年,劳伦斯和利文斯设计出了回旋加速器. 图22 回旋加速器的工作原理如图22所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m,电荷量为q,在加速器中被加速,加速电压为U.加速过程中不考虑相对论效应和重力作用. (1)求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比; (2)求粒子从静止开始加速到出口处所需的时间; (3)实际使用中,磁感应强度和加速电场频率都有最大值的限制.若某一加速器磁感应强度和加速电场频率的最大值分别为Bm,fm,试讨论粒子能获得的最大动能Ekm. 解得 (3)加速电场的频率应等于粒子在磁场中做圆周运动的频率,即 当磁感应强度为Bm时,加速电场的频率应为 粒子的动能 当fBm≥fm时,粒子最大动能由fm决定vm=2πfmR,解得 点评:要综合运用带电粒子在电场、磁场中运动的规律,尤其要理清电场、磁场的相互制约关系,才能正确求解.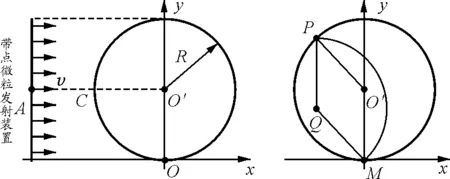
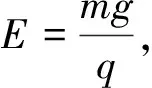

6 平行离开问题
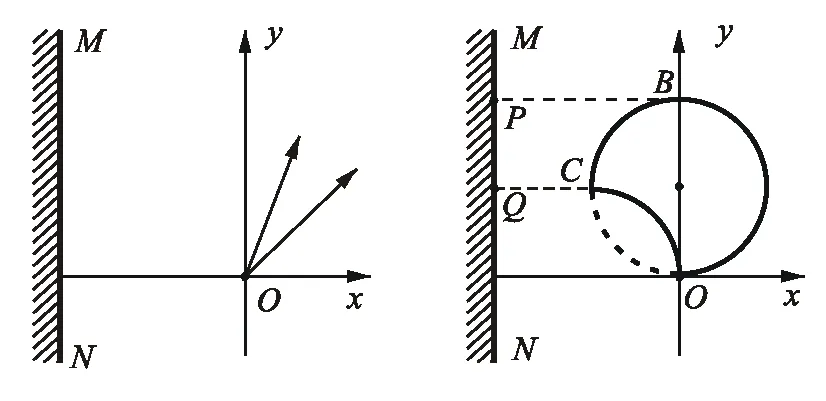

7 最小面积问题


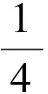
8 先散后聚问题
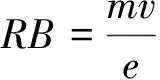

9 回归起点问题



10 粒子束缚问题

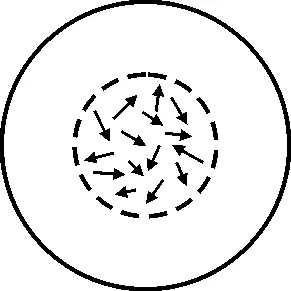


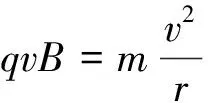
11 循环运动问题
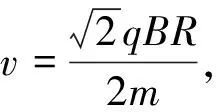
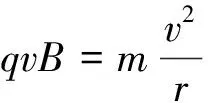

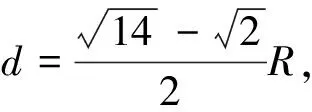
12 电磁综合问题