方圆管固定短芯棒拉拔工艺分析

刘 升，李浩进，王伯文

（1.武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，湖北武汉，430081；2.山西太钢不锈钢钢管有限公司，山西太原，030003）

ITER计划导体套管是一种形状为外方内圆的特殊管材，对其表面质量和尺寸精度要求很高。国外所研究的短芯棒拉拔模型[1]，是通过在芯棒出口端增加一定径带区域，并设置一个微小的台阶来抑制管材内径的弹性恢复，使内径尺寸精度达到规定的要求。目前国内通过有限元软件对材料大变形过程进行数值模拟分析[2－3]，并取得了很好的应用效果。为此，本文运用非线性有限元软件ABAQUS对ITER计划外方内圆导体套管成形工艺进行模拟仿真，得到稳定拉拔阶段的等效塑性应变、轴向和径向应力以及接触压力的分布规律，并分析了拉拔力和拉拔成形过程中能量的分布。

1 弹塑性有限元基本理论

1.1 有限元计算基本原理

拉拔套管的塑性成形问题是一个非常复杂的大弹塑性变形过程，由于其高度非线性难以收敛，故采用引入收敛因子的修正Newton－Raphson法。在有限元软件ABAQUS中运用增量加载法的修正Newton－Raphson算法进行非线性问题求解[4]，其迭代公式为

式中：Δu为位移增量为第n次迭代的切线刚度，N／m；φ为质点位移，m；R′为增量载荷，N；P为外力载荷，N；λn为收敛因子，λn＞0。

1.2 本构模型的定义

由于套管拉拔工艺中变形是多重非线性耦合问题，因此对材料建立适合于金属大变形的Canchy－Truesdell型本构模型[5－6]，其表达式为

式中：cijkl为材料的模张量；E为弹性模量，MPa；v为泊松比；H为加工硬化速率，m／s；α′为常数，塑性态为1，弹性态为0；δik、δjl为Kronecker数组；τ′ij、τ′kl为欧拉应力τij和τkl的有效应力分量。

1.3 摩擦属性的定义

拉拔套管成形过程中的接触问题需要计算摩擦，摩擦使得有限元数值计算求解的收敛变得困难。摩擦问题对金属流动有明显影响，同时还影响产品质量和模具寿命。由于经典的库仑摩擦模型的假设与现场的实际情况不相符合，为使模拟结果更加准确，选取修正的库仑摩擦模型[4]：

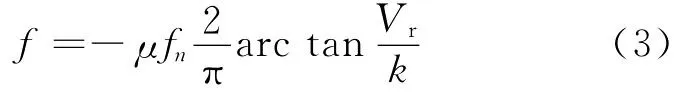
式中：μ为摩擦系数；fn为法向接触力，N；Vr为接触点处内管与模具表面的相对滑动速度，m／s；k为常数，k＝10－2～10－4。

2 模型建立与模拟参数设定

2.1 几何模型的建立

拉拔工艺为固定短芯棒两道次衬拉成形：□（外截面为方形）64／○（内截面为圆形）44.4→□59／○41→□54.2／○37.8，其中拉拔模角为12°；一道次衬拉成形的变形区长度为50 mm；二道次衬拉成形的变形区长度为46 mm。有限元模型中坯料选择为弹塑性体，而模具和芯棒选择为刚体；所有材料均各向同性，拉拔有限元模型如图1所示。

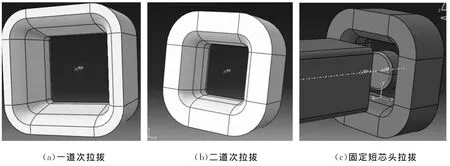
图1 拉拔有限元模型Fig.1 FEM model of drawing

2.2 材料模型的定义

套管的坯料采用316L钢种，其化学成分和力学性能如表1、表2所示。

表1 316L钢化学成分（wB／%）Table 1 Chemical composition of 316L steel

表2 316L钢力学性能指标Table 2 Mechanical properties of 316L steel

2.3 边界条件与载荷设置

在ABAQUS中建立拉拔三维有限元模型，结合现场实际情况进行设置：外模具和固定短芯棒均选择解析刚体且固定，限制其6个自由度；坯料为弹塑性体。载荷设置：定义坯料拉拔速度，同时选取坯料头部截面作为边界面来定义材料的拉拔力。

3 模拟结果与分析

3.1 拉拔工艺模拟网格划分

固定短芯棒拉拔成形的网格划分和模拟结果如图2所示。

图2 固定短芯棒拉拔模拟结果Fig.2 Simulation results of fixing short－plug drawing

3.2 等效塑性应变分析

图3为在稳定拉拔阶段时截取套管的等效塑性应变分布。等效塑性应变PEEQ是整个变形过程中塑性应变的累计结果，等效塑性应变大于0，表明材料发生了屈服。由图3（a）可看出，套管的PEEQ大于0，表明套管的外壁表面区域和内孔表面区域均发生了屈服。根据材料属性中定义的参数，使用剪切失效准则的判定依据是PEEQ达到1.0。由图3（b）可看出，稳定拉拔阶段坯料的轴向和径向PEEQ最大为0.492 3，可以判断套管处于屈服阶段且材料没有被破坏。

图3 稳定拉拔阶段时的等效塑性应变分布Fig.3 PEEQ of the stable drawing

3.3 拉拔成形的应力分析

图4为稳定拉拔阶段时的应力分布。由图4可看出，套管分别与模具和芯棒接触，外表面和内表面均受到挤压而变形。按照模具与管外表面是否接触，图4（a）为斜切套管截面，图4（b）为径向截面，可将其变形区分为非接触区、圆弧过渡区和定径带区。在圆弧过渡区，套管外表面受到压应力，内表面受到拉应力；在定径带区，主要由于摩擦力的影响，导管外表面比内表面承受更高的轴向流动阻力，套管外表面受到压应力，最大值达到621.53 MPa，套管内表面受到压应力，最大值达到293.01 MPa。由图4（b）可看出，应力集中在模具定径带和圆弧过渡区，模具在此两处较易发生磨损，芯棒上应力集中不是均匀分布的，磨损区域也不均匀，使得套管拉拔后可能产生缩径和大批量生产以后内径易出现椭圆度超标的缺陷。危险截面发生在模具定径带和套管外表面的接触部分，当外表面上的工作拉应力大于自身拉应力时，就会促使套管表面产生裂纹缺陷，这也是拉拔过程中易于表面产生微裂纹的原因，如果在伴随套管材料自身的塑性差、加工硬化程度大、拉拔模具表面润滑不好以及坯料外表面有缺陷时，拉拔成形出现裂纹的几率就会明显增加。

图4 稳定拉拔阶段时的应力分布Fig.4 Stress distribution of the stable drawing

3.4 拉拔成形中接触压力分析

套管的几何尺寸不是简单的基本几何形状，所以其在拉拔成形过程中所受到的接触压力在很大程度上影响了产品的尺寸精度和质量。图5为稳定拉拔阶段时的接触压力分布。由图5可看出，套管坯料与模具接触压力最大的地方是套管模具接触的圆弧过渡区，坯料在定径带区域时主要与芯棒接触。在这两个区域，套管外表面和内表面以及模具和芯棒均受到较大的接触压力，模具和芯棒是易磨损的地方，且芯棒磨损比模具磨损更严重，套管和模具接触时的最大接触压力为4 858 N，套管和芯棒接触时的最大接触压力为3 867 N。

3.5 拉拔套管的拉拔力分析

拉拔过程中拉拔力的大小一直在不断变化，本工艺中拉拔力与加载时间关系如图6所示。拉拔过程可分为初始拉入模具和稳定拉拔两个阶段。由图6可看出，在初始拉入模具阶段，随着套管坯料和模具发生接触，拉拔力逐渐增大；而稳定拉拔阶段，套管坯料和拉拔模具以及芯棒完全接触，拉拔力也趋于稳定变化，且波动范围较小，可以取波动范围内的平均拉拔力值作为本道次的最终拉拔力，计算所得到的稳定拉拔阶段的拉拔力为58.25 t。

图5 稳定拉拔阶段时的接触压力分布Fig.5 Contact pressure of the stable drawing

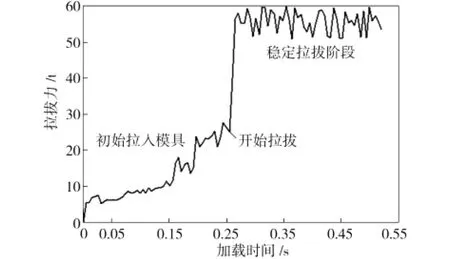
图6 成形过程的拉拔力Fig.6 Drawing force during forming process

3.6 拉拔过程中材料的能耗分析

图7为坯料在拉拔过程中的坯料动能、摩擦损耗能、塑性应变能和塑性损耗能曲线。由图7可看出，在初始拉拔时动能随着加载时间的延长而快速增加，拉拔稳定后即拉拔成形开始后坯料动能缓慢减小；初始拉拔时坯料没有接触，故其摩擦损耗能和塑性损耗能均为0，成形开始后摩擦损耗能和塑性损耗能均增加，且塑性损耗能高于摩擦损耗能，坯料虽有表面流动摩擦阻力，但其发生变形时仍然可以进行，而在整个拉拔过程中坯料的塑性应变能较小。由此可见，在拉拔过程中，一定会伴随着温度的变化，但温度并不影响材料加工性能；如果拉拔套管过长，则一定会影响套管内表面的加工精度和质量。

图7 拉拔过程中能量曲线Fig.7 Energy curves of drawing process

3.7 现场缺陷工艺分析及控制方法

拉拔一定次数后，在成品中产生了缩径和皱纹等缺陷。经过模拟计算，发现在拉拔过程中坯料的径向拉应力在某个时间会超过材料的抗拉强度，并且坯料和芯棒的接触区域所产生的接触压应力也有一个变化值。

缺陷产生的原因：缩进可能是由于拉拔过程中管坯材料容易产生加工硬化，导致拉拔模具磨损加剧，使得坯料拉拔完后内孔直径超过了允许的直径；而皱纹则可能是拉拔过程中坯料金属的单个雏晶接近于内表面分布，同样也接近于内表面变形和移动，其中一部分在管坯内部径向排挤出去，一部分向管坯壁厚方向移动，此时金属加工显微组织为纤维状时就会产生这种褶皱，并且这种缺陷随着管坯的变形程度增加而增多。解决的方法是：在模具工作面上衬以硬的高耐磨材料，并将坯料在拉拔前进行中间退火工艺处理。

为减少缺陷，本研究对工艺参数进行了修正，并对影响拉拔工艺参数进行了正交实验模拟，得到一组最优的拉拔工艺参数：模具锥半角为12°，圆弧过渡半径为25 mm，一道次变形区长度为46 mm，二道次变形区长度为45 mm，摩擦系数为0.1，拉拔速度为0.3 m／s，拉拔力为60.25 t。拉拔工艺参数改进后，在现场进行实际拉拔实验。结果表明，模拟分析后得到的优化方案比较有效，为套管拉拔工艺参数的选择提供了依据。

4 结论

（1）稳定拉拔阶段坯料的轴向和径向PEEQ最大为0.492 3，坯料虽在拉拔模具中发生屈服变形但没有被破坏。

（2）根据对拉拔成形过程中套管与模具和芯棒的接触压力分析，可得到模具与套管、芯棒和套管发生剧烈磨损的位置，拉拔过程中接触压力较大使得由于模具损耗导致套管大批量生产后易产生缩孔。

（3）初始拉拔时拉拔力增加较快，稳定拉拔时拉拔力波动范围较小，金属流动趋向稳定，此时提升拉拔速度，可以提高拉拔套管的生产效率；拉拔成形中，伴随摩擦损耗能、塑性损耗能、动能和塑性应变能的变化，虽会有温度的变化，但温度不影响材料加工性能；如果拉拔套管过长，则一定会影响套管内表面的加工精度和质量。

（4）修正后的拉拔工艺参数：模具锥半角为12°，圆弧过渡半径为25 mm，一道次变形区长度为46 mm，二道次变形区长度为45 mm，摩擦系数为0.1，拉拔速度为0.3 m／s，拉拔力为60.25 t。

[1] Alexandrove N.Analytical treatment of tube drawing with a mandrel[J].Int J Mech Sci，2001，215（5）：581－589.

[2] 刘国勇，朱冬梅，张少军，等.高温平板水雾冷却换热系数的数值分析[J].钢铁研究学报，2009，21（12）：24－27.

[3] 张光亮，张士宏，刘劲松，等.板材轧制过程轧制力刚塑性有限元快速计算[J].钢铁研究学报，2009，21（6）：32－33.

[4] 王国栋，赵德文.现代材料成形力学[M].沈阳：东北大学出版社，2008：34－83.

[5] Ienkiewicz O C Z，Taylor R L.有限元方法——固体力学[M].庄茁，岑松，译.北京：清华大学出版社，2006：30－80.

[6] 孟令启，徐如松，王建勋，等.中厚板轧制过程的数值模拟[J].钢铁研究学报，2009，21（3）：15－16.