板料回弹控制的成形工艺面多目标优化

阳湘安,阮 锋,许晓安

(1.广东技术师范学院机电学院,广东广州,510635;2.华南理工大学机械与汽车工程学院,广东广州,510640;3.广东技术师范学院科研处,广东广州,510635)

回弹是汽车覆盖件成形中的一个主要质量缺陷。出于汽车安全性和轻量化的要求,高强度板和铝合金板在汽车制造中得到大量应用,而其特殊的材料性能使得回弹问题更为突出[1-2]。

随着数值模拟精度和计算效率的提高,采用有限元数值方法结合优化策略可以很好地解决回弹问题[3]。但是,由于板料成形是一个高度非线性的过程,数值模拟无法直接给出待定设计参数与优化目标之间的显式函数关系,同时,数值模拟是一个非常耗时的计算过程,因此,需要建立优化代理模型来解决这一问题[4],如Kriging模型、响应面(RSM)模型和径向基函数(RBF)神经网络模型等。

源自统计理论的Kriging模型是一种估计方差最小的无偏估计模型,能够拟合非常复杂的函数关系,但是其计算时间较长,对于多设计变量模型而言其计算精度较低,且形式较为复杂,因而在板料成形优化中应用较少;基于统计理论的响应面法能够构建多维设计空间中优化目标与设计变量的显式函数关系,是一种常用的代理模型构建方法[5],但是,当问题的非线性非常复杂时,采用响应面法往往难以得到正确的优化解,在多项式的阶数较高时,还容易出现过拟合现象;径向基函数神经网络模型在样本数量足够多的情况下能够有效地拟合目标函数与设计变量之间的非线性关系[6]。Jin[7]等采用4种常用的优化代理模型对14个不同类型的测试算例进行对比分析后发现,在同时考虑模型精度和鲁棒性的情况下,径向基函数神经网络模型是最为可靠的。

本文拟采用实验设计和径向基函数神经网络建立基于回弹控制的板料成形工艺面多目标优化的代理模型,并在均匀实验设计的基础上再次采用该方法对端部的实验方案样本点进行加密,以提高优化的精度和稳定性。

1 问题的描述

1.1 目标函数的选择

板料成形的优化目标主要是控制板料的回弹,对回弹的量化评判非常重要。直观的评判准则是工件回弹前后对应节点的位移偏差,这种评判准则与回弹的概念相符,在有限元数值仿真中应用较多[3],如式(1)所示:

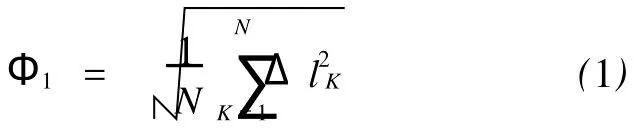
式中:Φ1为回弹目标函数;N为工件节点总数;ΔlK为节点位移偏差。

由于板料塑性变形的增大将导致回弹的减少,因此有些学者将板料的等效塑性应变作为回弹的评判准则[8],以等效塑性应变裕度Φ2来表征回弹,如式(2)所示:

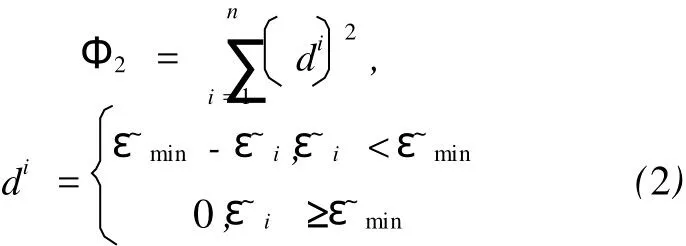
式中:n为板料单元总数为板料第i个单元的等效塑性应变为最小等效塑性应变。式(2)表明,对于第i个单元,当其等效塑性应变小于最小等效塑性应变时,板料塑性变形不够充分,目标函数值不为0;否则,板料塑性变形很充分,目标函数值为0。但是,由于回弹量的大小是一个与应力和应变相关的量,这种回弹评判方式是不全面的。

由于回弹的过程也是板料内能的释放过程,因此,在忽略系统与外部环境的热交换以及系统内热损失的情况下,有些学者以板料的弹性内能变化率Φ3作为回弹的评判准则,如式(3)所示:

式中:σij为应力张量;Dij为伸长率张量;Ω为积分域。但是,板料的弹性内能变化率反映的是整个板料体积的内能变化,而且与式(1)相比,其对回弹的表达不够直观。

朱东波等[9]提出以回弹能Φ4作为回弹的评判准则,其实质也是一种基于微分几何的曲面能量表达方式[10],如式(4)所示:

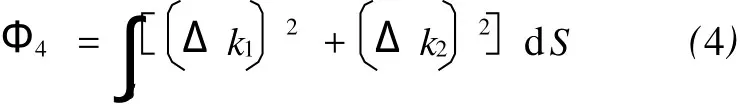
式中:Δk1和Δk2为板料两个主方向的主曲率偏差;S为面积分域。曲面回弹能的概念将板料的几何参数和曲面能量结合起来,对于回弹的量化评判是比较合理的。但是在实际应用中,如何简单而有效地计算出节点的主曲率偏差仍然是一项有待研究的工作。

综上所述,以Φ1作为回弹评判准则符合实际中对回弹的直观认识,且其表述简单、便于应用。但是,为了保证产品的刚度,往往要求其具有一定的塑性变形,虽然这种对产品塑性变形的要求可以作为约束条件来处理,但考虑到塑性变形程度与回弹量大小有很大的关系,因而,以回弹目标函数Φ1和等效塑性应变裕度目标函数Φ2共同表征回弹更为合理。

1.2 约束条件的确定

在板料成形过程中,容易出现的质量问题主要是板料的破裂、起皱和塑性变形不足。考虑到回弹的大小与塑性变形的程度密切相关,可以将塑性变形不足问题作为目标函数来处理。

对于破裂和起皱,通常可以采用成形极限图(FLD)来表征,以板料所有有效单元的最终应变值位于破裂和起皱极限间的成形安全区间为约束条件,即:

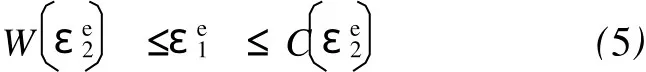
然而,获得成形极限曲线所需的实验工作量很大,实验过程中影响曲线精度的因素也很多。考虑成形缺陷的发生总与板料变形后局部过度的减薄或增厚有关,因此,一些研究者从板料厚度变化角度出发提出了成形极限判据[11],即以单元最大增厚率和最小减薄率来判断板料的起皱和破裂,如式(6)和式(7)所示:

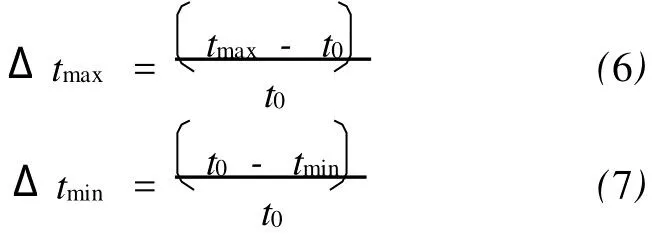
式中:Δtmax为最大增厚率;Δtmin为最小减薄率;tmax为最大单元厚度;tmin为最小单元厚度;t0为初始板厚。

1.3 设计变量的确定

模具型面一般包括成形部分型面和工艺面。对于复杂工件,采用少量的几何参数难以完整地描述成形部分型面,而如果以网格节点的坐标作为设计变量,则由于设计变量数目太大而使优化计算时间很长,甚至难以得到合理的优化结果[12]。对于工艺面来说,由于其几何性质较为简单,参数化实现已较为成熟,因此,本文选择工艺面的若干几何参数作为设计变量。

2 基于代理模型的优化过程和策略

从优化计算的效率出发,采取“实验设计—建立代理模型—多目标优化算法求解”的分步优化策略。为了建立优化问题的代理模型,一般可以采用均匀实验设计方法确定设计空间中均匀散布的若干实验点,以便用最少的实验次数获得尽可能充分的信息。为此,采用优化拉丁超立方实验设计方法将每个设计参数的设计空间均匀划分为M×M的方阵,然后在其中随机生成不同行不同列的M个采样点。

考虑到板料成形的非线性特征,代理模型采用径向基函数(RBF)神经网络模型,其表达式为:

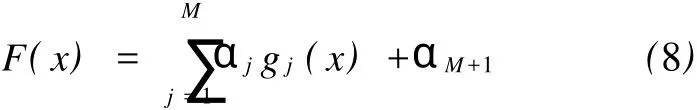
径向基函数是某种沿径向对称的标量函数。一般情况下任何函数都可以表示成一组径向基函数的加权和,所以采用RBF神经网络模型可以实现从输入样本到输出函数之间的一种非线性映射。

由于成形工艺面优化问题的非线性特征明显,其目标函数具有多峰性,因此,采用的优化算法应该能求出其全局最优解。对于多目标优化,非支配排序遗传算法NSGA-II比较成熟。NSGAII采用小生境分组技术以获得在可行设计空间中均匀分布的候选解集,增加群体的多样性;选择算子采用快速非支配排序分级技术和同级别个体的拥挤距离排序技术,以提高个体选择的效率;引入精英保留机制,定义当前种群的非劣个体集合为精英解集,并参与到下一代个体的种群进化竞争,以保证优良个体的遗传,从而跳出局部优化解,并最终得到全局最优解。

3 算例

以车身侧外板为例进行成形工艺面多目标优化,车身侧外板的有限元模型如图1所示。板料尺寸为1 217 mm×790 mm×0.8 mm,共划分为9 638个单元,单元类型为Belytschko-Tsay(BT)壳单元,BT单元是基于Mindlin-Reissner假设的板壳单元,采用了基于随体坐标系的应力计算方法,不必计算费时的Jaumarm应力,因而具有很高的计算效率。考虑到板料的相对厚度较小,厚度方向上只取5个积分点。板料材质为高强度板DP600,以三参数Barlat材料模型描述其各向异性。板料的弹性模量为207 GPa,泊松比为0.28,硬化指数为3。在板料的切边回弹分析中采取全积分方案以更精确地计算回弹。

图1 车身侧外板成形的有限元模型Fig.1 Finite element model of side wall panel forming

工艺面的轮廓曲线如图2所示,设计变量取为圆角过渡处半径R1、R2和侧面的倾斜角α。

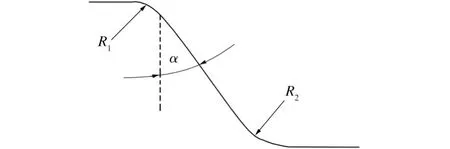
图2 工艺面轮廓曲线Fig.2 Profile of addendum

车身侧外板成形工艺面的优化问题可描述为:

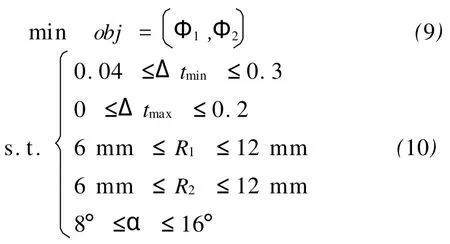
约束条件的边界取值根据生产实践中的经验数据以及设计规范得到。

4 优化结果及分析

值得一提的是,在经过32个训练样本回归建模并采用NSGA-II算法进行优化求解后发现,设计变量的优化结果中总有不少解处于其取值范围的两端附近,而对这些解进行验证后却发现其存在较大误差。可以采取次数更多的均匀实验设计来解决这一问题,但这样却增加了计算工作量。一个更好的解决办法是对均匀实验设计方案进行改进,即在设计变量取值范围的端部区域再次采取均匀实验设计方法以加密端部的实验点,从而建构一个合理的代理模型。本文中两端区域通过再次均匀实验设计后,实验点各增加2个。

为了验证RBF神经网络代理模型的优化效果,本文还建立了基于优化拉丁超立方实验设计的响应面代理模型,设计变量取值范围两端的实验点未加密,同样采用NSGA-II算法进行优化求解。

对改进前后的RBF神经网络和响应面代理模型进行求解时,初始种群规模皆为12,经过20代遗传优化后得到的Pareto解集如图3所示。

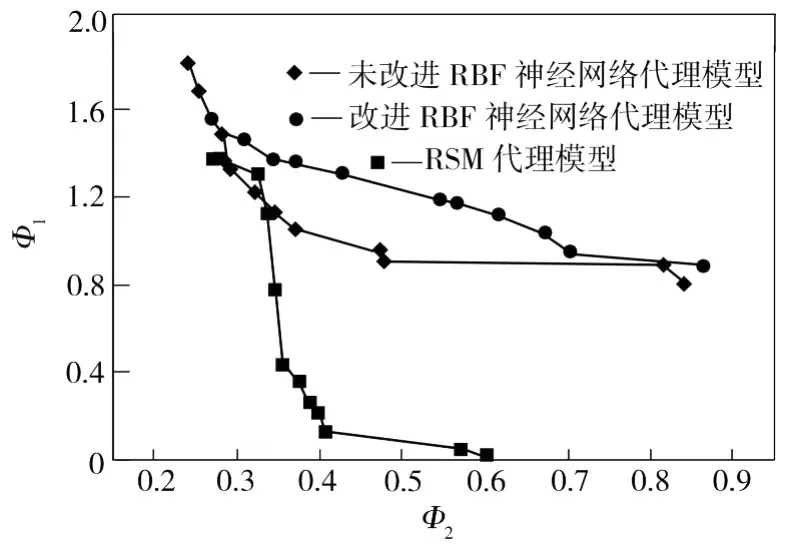
图3 代理模型的Pareto解集Fig.3 Pareto solutions of surrogate models

从图3中可以看出,基于RSM代理模型的Pareto解集与基于RBF神经网络代理模型的Pareto解集的分布趋势差异很大,而两个基于RBF神经网络代理模型的Pareto解集的分布趋势基本相同,但曲线中部的Pareto解差异相对较大。为了进一步比较各模型的优化效果,在其Pareto解集中分别随机抽取满意解,进行有限元增量的数值模拟实验,结果如表1所示。

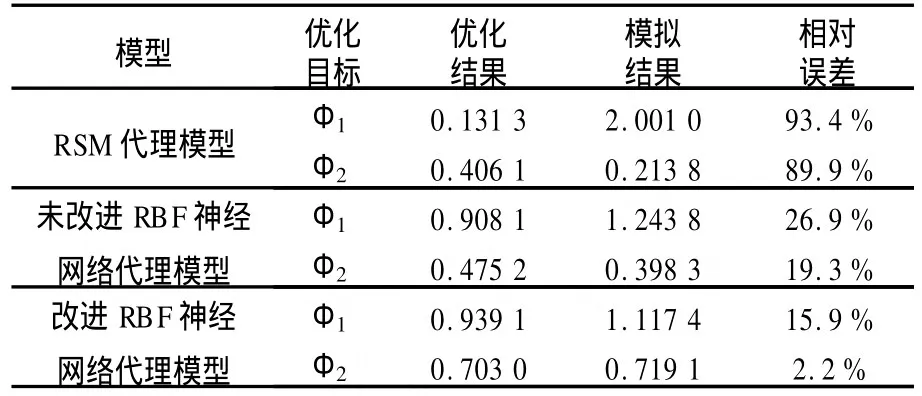
表1 优化结果的误差比较Table 1 Error comparisons of optimization results

从表1中可以看出,基于RSM代理模型的优化精度很低,回弹目标函数Φ1的相对误差高达93.4%,等效塑性应变裕度目标函数Φ2的相对误差也达到89.9%,这主要是因为工艺面优化问题的非线性特征明显,RSM代理模型难以精确地描述原模型;基于RBF神经网络代理模型的优化精度均较高,而且经过改进后,RBF神经网络代理模型的优化精度又得到较大提高。与实验设计中回弹量最大的方案相比,采用基于改进RBF神经网络代理模型的优化方案进行数值模拟实验,板料回弹量由6.266 6 mm降至1.117 4 mm,减少了5.149 2 mm,这也表明了设计变量取值范围端部区域加密方案的有效性。

5 结语

本文建立了基于回弹控制的成形工艺面多目标优化模型,采用“优化拉丁超立方实验设计—径向基函数神经网络代理模型—NSGA-II算法”的优化策略对其进行求解。在均匀实验设计的基础上对设计变量取值范围的两端区域再次进行均匀实验设计,以增加少量实验次数为代价,获得了较高的优化精度。算例分析表明,本文建立的成形工艺面多目标优化模型是合理的,采取的优化策略是有效可行的。

[1] Hisashi H,Takeo N.Recent trends in sheet metals and their fo rmability in manufacturing automotive panels[J].Materials Processing Technology,1994,46:455-487.

[2] 龙江启,兰凤崇,陈吉清.车身轻量化与钢铝一体化结构新技术的研究进展[J].机械工程学报,2008,44(6):27-35.

[3] Liu Wei,Yang Yuying,Xing Zhongwen,et al.Spring back control of sheet metal forming based on the response-surface method and multi-objective genetic algorithm[J].Materials Science and Engineering:A,2009,499(1/2):325-328.

[4] 谢延敏,于沪平,陈军,等.基于代理模型的板料成形优化技术进展[J].塑性工程学报,2006,13(2):20-24.

[5] Naceur H,Ben-Elechi S,Batoz J L,et al.Response surface methodology for the rapid design of aluminum sheet metal frming parameters[J].Materials and Design,2008,29(4):781-790.

[6] 穆雪峰,姚卫星,余雄庆,等.多学科设计优化中常用代理模型的研究[J].计算力学学报,2005,22(5):608-612.

[7] Jin R,Chen W,Simpson TW.Comparative studies of metamodeling techniques under multiple mode ling criteria[J].Journal of Structural Optimization,2001,23(1):1-13.

[8] 郑超,刘全坤,胡龙飞,等.基于回弹控制的汽车横梁拉延成形工艺多目标优化研究[J].合肥工业大学学报:自然科学版,2008,31(1):89-92.

[9] 朱东波,马雷,李涤尘,等.复杂形状板料冲压件回弹评价指标研究[J].机械科学与技术,2000,19(6):953-955.

[10] 柳晓燕,冯峰.基于能量优化的NURBS曲面几何特征修改[J].计算机工程与应用,2008,44(26):41-44.

[11] 陈劼实,周贤宾,刘长丽.数值模拟中应用最小厚度准则预测板料成形极限[J].中国机械工程,2006,17(S1):67-70.

[12] Shi Xiaoxiang,Chen Jun,Peng Yinghong,et al.A new app roach of die shape optimization for sheet metal forming processes[J].Journal of Materials Processing Technology,2004,152(1):35-42.