伺服阀主阀芯的建模与仿真
黄 浩,崔润哲,陈奎生
(武汉科技大学机械自动化学院,湖北武汉,430081)
电液伺服阀具有体积小、功率放大率高、直线性好、死区小、响应速度快、运动平稳以及能适应模拟量和数字量调制等优点,在冶金、航空等行业中都得到了广泛的应用[1]。
本文针对某型伺服阀,在主阀芯阀口开口大小一定、压差不同的情况下,对其内部流场进行数值模拟分析,并与理论计算结果进行比较。
1 伺服阀主阀芯流场的模拟仿真
1.1 网格划分
由于油液在伺服阀阀口的流动情况非常复杂,阀口既是压力变化最大的区域,又是结构尺寸最小的区域。因此,根据阀内部流道的几何尺寸,应对阀口区域和流道拐角的网格进行细化。正常情况下,紧靠管道壁面区域流体的速度梯度很大,而管路中心的速度梯度相对较小,因此在网格划分时,应在壁面附近加入一个细化网格的边界层,以增大靠近壁面区域的网格密度,使速度梯度和压力梯度能更清晰地显示,流道中心的网格密度可以适当降低。
某型伺服阀主阀芯直径为30 mm,采用Gambit对其进行三维网格划分[2],如图1所示,图1(a)上端为进口P,下端为出口A;图1(b)为图1(a)中圆圈标示的阀开口处局部放大网格图。
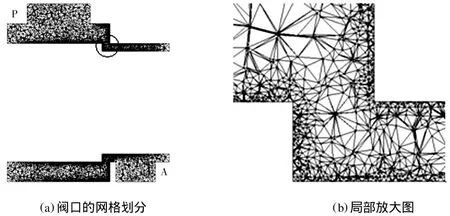
图1 伺服阀主阀芯阀口网格划分图Fig.1 Main spool grid of servo valve
1.2 初始条件与边界条件
在流场分析软件中导入网格模型后,根据实际情况对求解器作如下参数设定:采用非耦合方式、3D轴对称、非定常流、导入能量方程,黏度模型为湍流,流体介质选取32号液压油,初始条件采用全流域初始化[3]。
仿真的边界条件为:进油口P为压力入口边界条件,出油口A为压力出口边界条件,出口压力设定为1 M Pa,进口压力分别设定为1.1、1.5、2.0 M Pa。仿真计算中,流体和流动状态分别设定为单相流和紊流,流体接触的边界为静止壁面。
2 仿真结果与分析
在阀开口为0.5 mm、压差不同的情况下,对模型进行仿真计算。阀口处流体的压力及速度仿真结果如图2~图4所示。流场仿真的相关数据如表1所示。
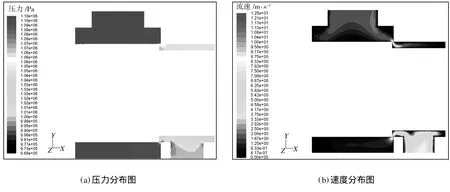
图2 进出口压差为0.1 MPa时阀口流体的压力和速度分布图Fig.2 Pressure and velocity distribution at the pressure difference of 0.1 MPa
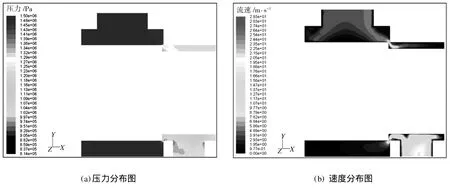
图3 进出口压差为0.5 MPa时阀口流体的压力和速度分布图Fig.3 Pressure and velocity distribution at the pressure difference of 0.5 MPa
从图2~图4中可以看出,主阀芯进口P处的压力和流速分布都比较均匀;而出口A处压力分布比较均匀,流速分布不均匀。整个P腔的压力和流速分布也很均匀,靠近阀口时,流速开始逐渐增大,压力开始逐渐降低,流体的压力水头转换成了速度水头,符合流体运动的流量连续性定理和能量定理。
由于附面层对流速的影响,阀口靠近阀芯壁和阀套壁附近流层的流速非常小。阀口出口区域出现了射流,中心的流速最高。由于阀口的压力损失,出口处的流体压力明显降低。在A腔里,靠近P口端的压力比靠近A口端的压力要高,这是由于油液要通过一个同心圆环状的流动到达A口端,由此造成的压力损失所导致的。在阀口出口附近,形成了一个低压区。从表1中可以看出,当系统具有足够背压时,靠近A口的这个低压区的压力也远高于一个标准大气压,不会造成气穴现象。从图2~图4中的流速仿真图中可以看出,当压差增大时,靠近A口端的流体经过阀口会逐渐形成一个主液流,这也符合液体流动的规律,即流体运动遵循最小流动损失。阀口压差为0.5 M Pa,阀开口为0.5 mm时,阀口压力局部放大仿真图如图5所示。由图5中可以看出,阀口附近会产生一个低压区。
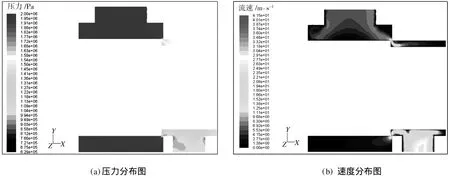
图4 进出口压差为1 MPa时阀口流体的压力和速度分布图Fig.4 Pressure and velocity distribution at the pressure difference of 1 MPa

表1 压差不同时阀口流场的仿真结果Table 1 Parameters of flow field simulation at different pressures

图5 压差为0.5M Pa时阀口处的压力场局部放大仿真图Fig.5 Simulation of pressure distribution of the local amplification at the pressure difference of 0.5 M Pa
3 仿真结果与理论计算值的比较
伺服阀主阀芯阀口的理论压力-流量公式为[4]:

式中:Q为流过阀口的质量流量,kg/s;Cd为流量系数,一般取0.5~0.61;A为阀口面积,mm2;ΔP为阀口前后的压差,Pa;ρ为介质的密度,kg/m3。
对阀开口为0.5 mm、压差分别为0.1~1.0 M Pa时的流场进行仿真,得出阀口流体的质量流量仿真数据,并与式(1)计算所得Cd分别为0.61、0.5时阀口流体的质量流量数据进行比较,结果如图6所示。由图6中可见,仿真结果与理论计算值之间非常接近,表明仿真结果具有准确性。
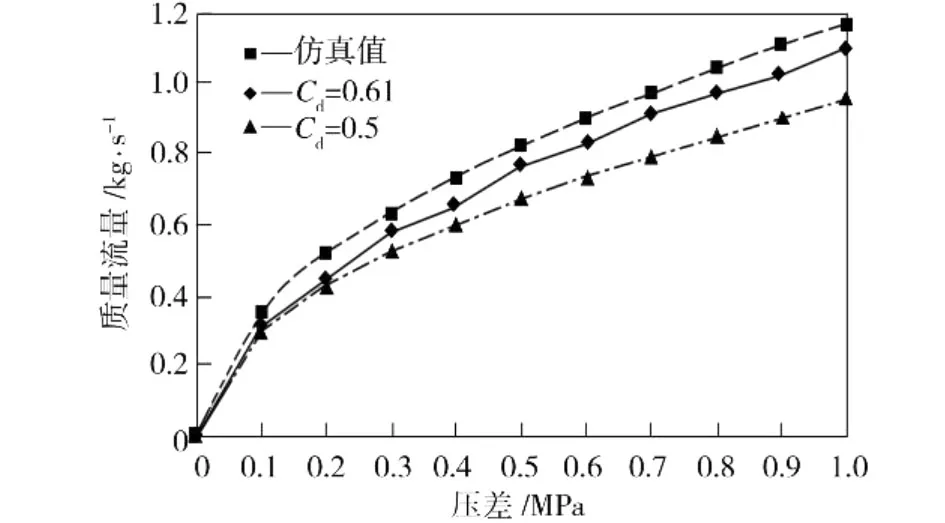
图6 阀开口为0.5 mm时阀口流体的质量流量Fig.6 Fluid mass flow of valve orifice for 0.5 mm aperture
4 结语
对某型伺服阀主阀芯流场进行了仿真分析,仿真数据和理论计算值对比表明,运用流场仿真软件对主阀芯流场的仿真是正确的。通过仿真,可以清楚地观察到阀腔内速度场和压力场的变化,可以迅速、可靠地分析具有复杂管道的伺服阀的特性,为分析和计算各种不同因素如直径和长度、倾斜角度、压力和流量等对阀的流场的影响提供依据,以便对伺服阀进行结构优化设计。
[1] 陈奎生.液压与气压传动[M].武汉:武汉理工大学出版社,2001.
[2] 黄浩,姚笔,金晓宏,等.动圈式伺服阀内部流场的数值模拟[J].武汉科技大学学报,2010,33(2):214-218.
[3] 韩占忠,王敬,兰小平.Fluent流体工程仿真计算与应用[M].北京:北京理工大学出版社,2004.
[4] E·约翰芬纳莫尔,约瑟夫·B·弗朗兹尼.流体力学及其工程应用[M].钱翼稷,周玉文,译.北京:机械工业出版社,2005.

