基于静特性分析的环面节流静压气体球轴承参数设计

郭良斌,彭宝林,王 卓,宣立明

(武汉科技大学机械自动化学院,湖北武汉,430081)

静压气体球轴承是空间飞行器多自由度仿真气浮台的关键部件之一[1-2],其工作原理是依靠压缩空气在球与球窝之间形成气膜,使仿真平台浮起,从而满足近似无摩擦的相对运动条件[3-4]。多自由度仿真气浮台可以用来研究飞行器的编队飞行、轨道机动和空间交会等技术问题[5]。近年来,仿真气浮台多采用环面节流多孔闭式气体球轴承[6],该类轴承具有整体球窝面,球窝中心没有与环境大气相通的排气孔。环面节流多孔闭式气体球轴承具有能够在大范围供气压力下稳定工作的优点[7],是随着国际微小卫星研究兴起而出现的一种静压气体球轴承新结构形式。

针对小孔节流多孔开式气体球轴承的非线性静态有限元气体润滑方程组提出的“比例分割算法”[8],同样适用于闭式静压气体球轴承的静态有限元方程组的求解,且可以获得满意的静特性计算解[9]。环面节流多孔闭式球轴承的几何参数包括球窝外包角、供气孔包角、供气孔数、供气孔直径以及轴承半径共5个参数。几何参数对轴承的性能有着极大的影响,设计合理的几何参数能使轴承具有良好的工作性能。为此,本文按照优先考虑静刚度指标以及兼顾流量、承载力指标的设计原则,采用保角变换有限元法研究环面节流多孔闭式气体球轴承几何参数设计的基本过程,并详细讨论了球窝外包角、供气孔包角、供气孔数和供气孔直径对轴承静特性的影响。

1 数学模型描述

图1为气体球轴承所在的球面坐标系。静压球面气体润滑静态无因次可压缩雷诺润滑方程为

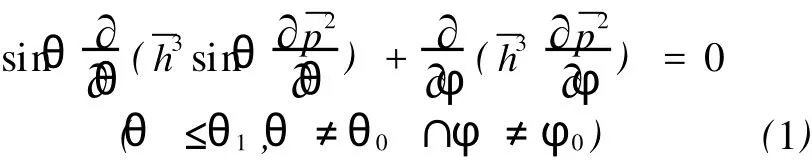
式中:θ、φ为气膜中任一点的球面坐标,θ0、φ0为供气孔所在的球面坐标为气膜中任一点的无因次厚度,=h/e(e为球心的起浮高度,μm);为气膜中任一点的无因次压力,=p/Ps(Ps为轴承供气压力,M Pa)。

设静压气体球轴承的n个供气孔沿圆周均匀分布,且气浮台工作时球体不受水平力的作用,因此球轴承工作时球心只沿铅垂方向运动,轴承对称于过球心的铅垂线。计算时,可取1/2n球窝面(图1阴影部分)为求解域。

为方便求解,对式(1)进行保角变换。变换式通常取α=ln tan(θ/2),dα=dθ/sinθ,引入无因次压力平方,代入式(1)后,将其变换成静态雷诺气体润滑方程:

图1 气体球轴承所在的球面坐标系Fig.1 Spherical coordinates of spherical gas bearing

值得注意的是,当θ=0时,保角变换式不存在。为了解决变换过程中的这一数学难题,引入图1中的无限小半径Ra。当Ra趋于无穷小时,可认为气膜求解域等同于Ra～Rb的球面区域。经保角变换后,该求解域变为标准矩形,如图2所示。通过求得半径为Ra的邻域边界上的压力来近似得到θ=0点的压力[9]。

定义整个研究域的边界为Γ,图2给出了组成Γ的三类边界,其对应的边界条件为:①在大气边界ba上为无因次的大气压;②在供气孔区域Ah及边界bh上为无因次的供气孔出口压力;③在对称边界bs上边界的正法线。有限元离散过程见文献[9]。

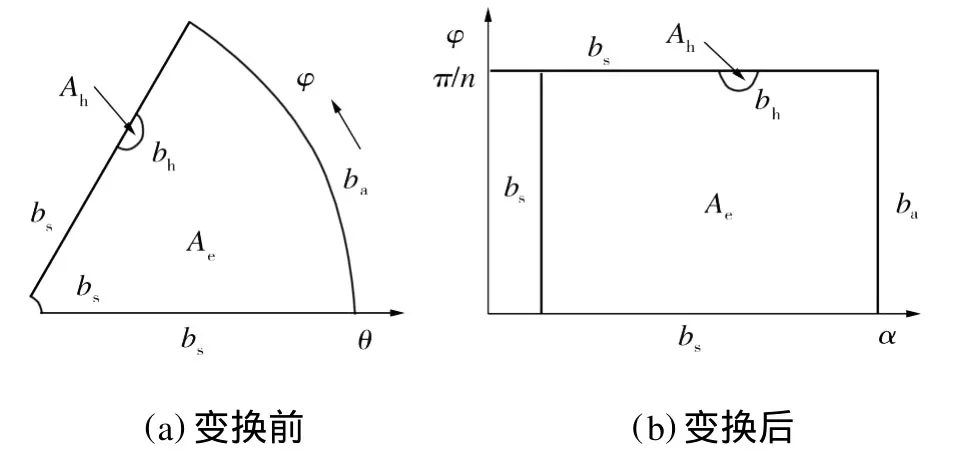
图2 保角变换前后的研究域及边界Fig.2 Calculating domains and borders before and after conformal transformation

2 闭式气体球轴承几何参数设计

将气膜压力的铅垂分量沿球面积分,得到轴承铅垂方向上的承载力[8]:

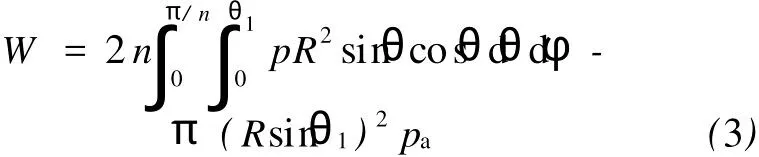
用差分代替微分,得到轴承静刚度的近似值:

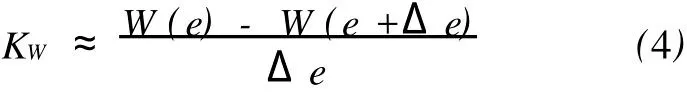
从小孔出流公式中,得到轴承气体质量流量[8](或换算为标准状态下的体积流量):

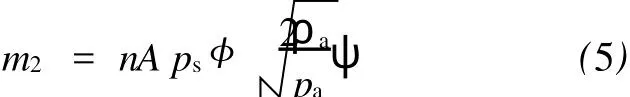
式中:m2为通过供气孔流入气膜间隙的气体质量流量,kg/s;n为供气孔数,个;A为环面节流面积,m2;φ为小孔流量系数;ρa为环境大气密度,kg/m3;ψ为节流压力比(供气孔出口压力pd与供气压力ps的比值)确定的函数。即

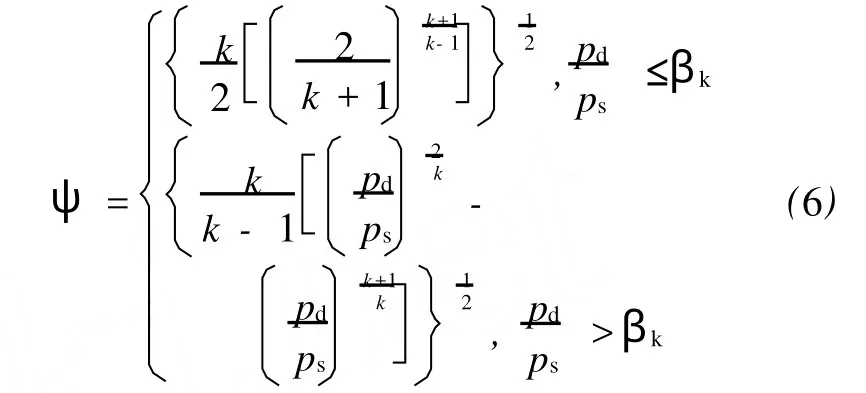
式中:βk为临界压力比,βk=0.528;k为比热比,对于空气,k=1.4。

在轴承的静特性(承载力、流量和静刚度特性)指标中,对于气浮仿真台的使用场合,轴承的静刚度是最重要的指标。轴承的静刚度越大,气浮台在受到外界干扰力作用时球心起浮高度的变化越小,物理仿真结果越稳定,越接近实际空间飞行的状态。另外,设计时应兼顾承载力和流量特性,承载力特性太差,将需要增大轴承设计直径,或者提高轴承的供气压力来弥补,前者将增加精密加工工作量而加大轴承的制造成本,后者则增大气体的耗气量。

2.1 球窝外包角对轴承静特性的影响

表1为闭式气体球轴承的几何和工作参数。保持其他几何参数不变,可计算球窝外包角为25°～75°时的轴承静特性,如图3所示。计算时球心的起浮高度从5μm一直计算到供气孔壅塞,并将质量流量转化为标准状态下的体积流量。由图3(a)可看出,增加球窝的外包角能够明显地增大轴承的承载能力;在相同的球心起浮高度时,不同的球窝外包角产生的承载力差异极大,因此球窝的外包角是决定轴承承载力性能的一个关键参数。由图3(b)可看出,随着球窝的外包角增大,在相同的球心起浮高度时,轴承消耗的气体体积流量减小。一般情况下,气体球轴承工作时,球心起浮高度为5～50μm。由图3(c)可看出,在开始阶段,随着球窝外包角的增加,静刚度曲线整体上移,最大静刚度明显上升;当球窝外包角超过65°时,随着外包角的增加,轴承在工作起浮高度范围内的静刚度反而下降。综上所述,为了使轴承具有较佳的静特性,外包角的设计值选择55°～65°时较为合理,此时轴承具有近似最大的静刚度、可观的承载能力以及相对低的气体耗气量。

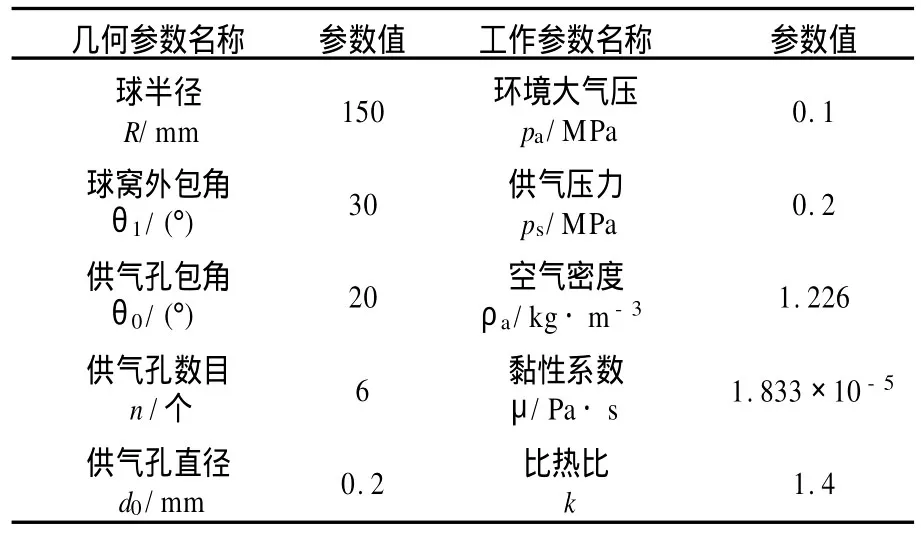
表1 闭式气体球轴承参数Table 1 Parameters of spherical gas bearing

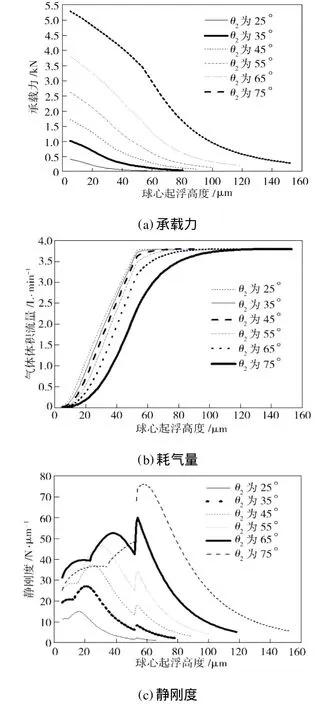
图3 不同球窝外包角下轴承的静特性Fig.3 Static characteristics of gas bearing at different outer wrap angles

2.2 供气孔包角对轴承静特性的影响

按表1中参数更改球窝的外包角为65°,保持其他几何参数不变,可计算供气孔包角为10°～50°时的轴承静特性,如图4所示。由图4(a)可看出,供气孔包角从10°增至40°时,轴承的承载力相差不大;当供气孔包角增至50°时,轴承的承载力略有下降。供气孔包角对承载力的影响远低于球窝外包角对承载力的影响。由图4(b)可看出,在开始阶段,当供气孔包角从10°增至40°时,轴承消耗的体积流量基本不变;当供气孔包角增至50°时,轴承消耗的体积流量略有下降。由图4(c)可看出,当供气孔包角从10°增至40°时,轴承的静刚度曲线整体上移,最大静刚度随之增加至近似最大;当供气孔包角继续增加时,轴承在工作起浮高度范围内的静刚度稍有下降。综上所述,供气孔包角设计值选择40°～50°时较为合理,此时轴承具有近似最大的静刚度、良好的承载力特性以及相对低的气体耗气量。

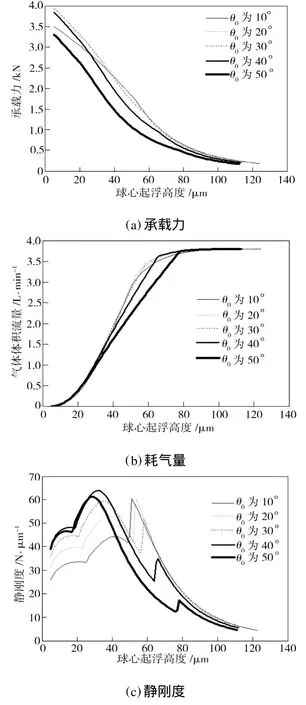
图4 不同供气孔包角下轴承的静特性Fig.4 Static characteristics gas bearing at different wrap angles of orifice

2.3 供气孔数对轴承静特性的影响

按表1中参数更改供气孔包角为40°、球窝外包角为65°,保持其他几何参数不变,可计算供气孔数为3～10时的轴承静特性,如图5所示。由图5(a)可看出,随供气孔数的增加,轴承的承载力相应增加。由图5(b)可看出,随着供气孔数的增加,轴承消耗的气体流量明显增加。由图5(c)可看出,当供气孔数从3增至5时,轴承静刚度的峰值基本保持不变,只是静刚度曲线峰值对应的球心浮起高度稍有不同;随着供气孔数的进一步增加,轴承的最大静刚度反而下降。综上所述,环面节流闭式气体球轴承的供气孔数为5～6时较为合理,此时轴承的承载力和耗气量处于适中的水平,而轴承的最大静刚度近似最大,综合性能较佳。

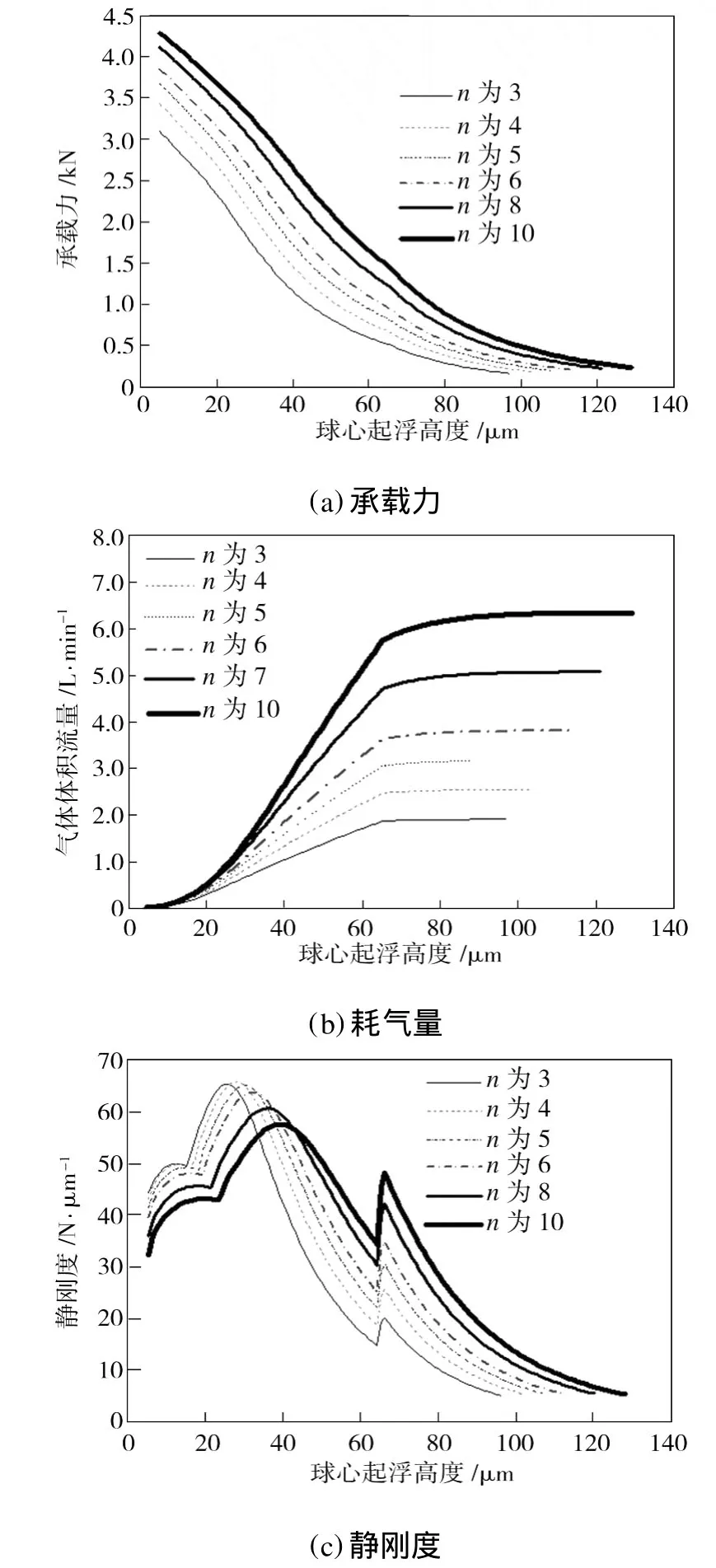
图5 不同供气孔数下轴承的静特性Fig.5 Static characteristics of gas bearing at different orifice numbers

2.4 供气孔直径对轴承静特性的影响

按表1中参数更改供气孔包角为40°、球窝外包角为65°、供气孔数为5,保持其他几何参数不变,可计算供气孔直径为0.2～1.0 mm时的轴承静特性,如图6所示。由图6(a)可看出,供气孔直径对轴承承载力特性影响相对较小,不同供气孔直径的轴承可以实现的最大承载力基本相同;随着球心起浮高度的增加,供气孔直径大的轴承承载力下降较慢,而供气孔直径小的轴承承载力下降较快。由图6(b)可看出,随供气孔直径的增加,轴承消耗的气体体积流量明显增加。由图6(c)可看出,随供气孔直径的增加,在工作起浮高度范围内,轴承的最大静刚度显著下降。综上所述,环面节流闭式气体球轴承的供气孔直径为0.4～0.6 mm时较为合理,此时轴承保持了较好的静刚度以及适中的承载力特性和耗气量。

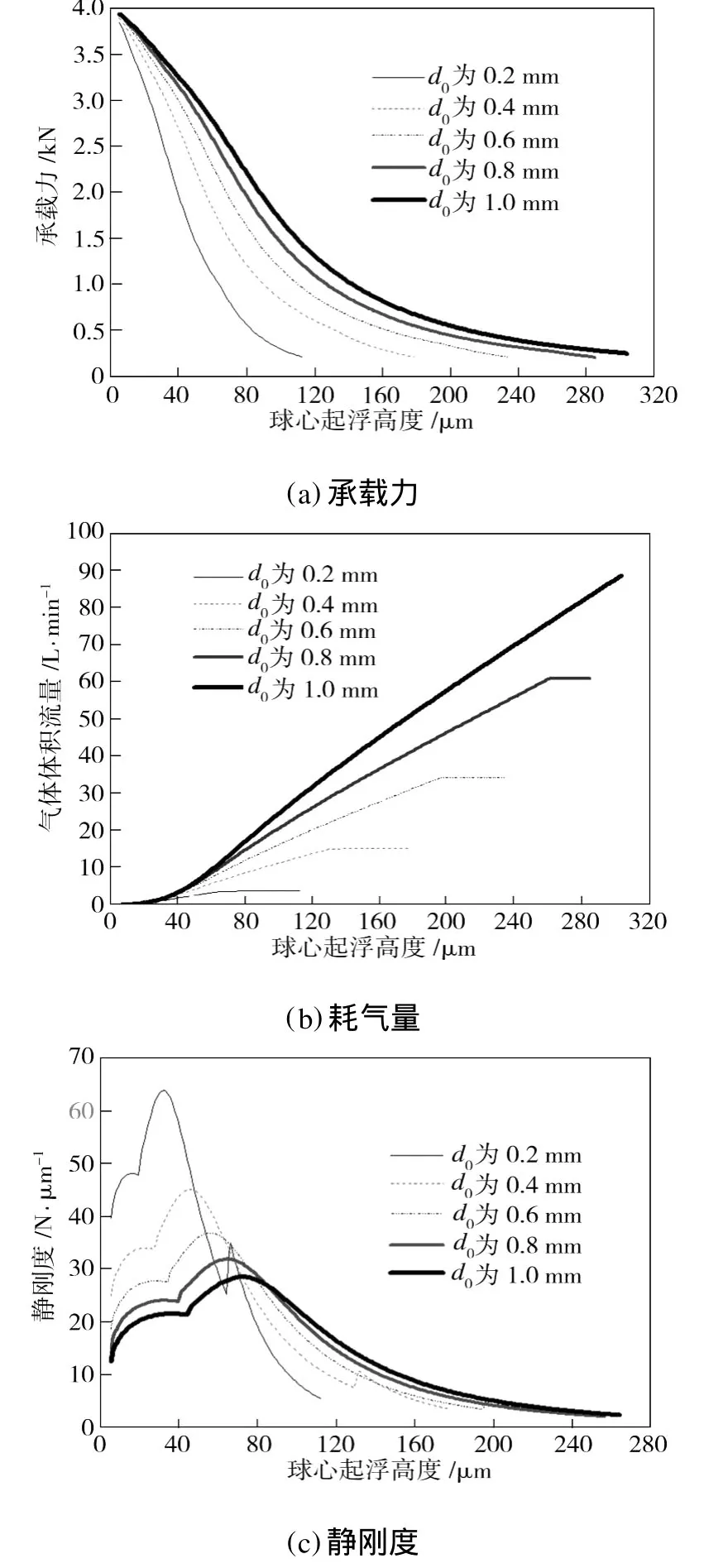
图6 不同供气孔直径下轴承的静特性Fig.6 Static characteristics of gas bearing at different orifice diameters

2.5 闭式球轴承几何参数的推荐取值范围

综合2.1～2.4节的分析,为使轴承具有尽可能好的综合性能,表2为闭式气体球轴承的几何参数推荐取值范围。

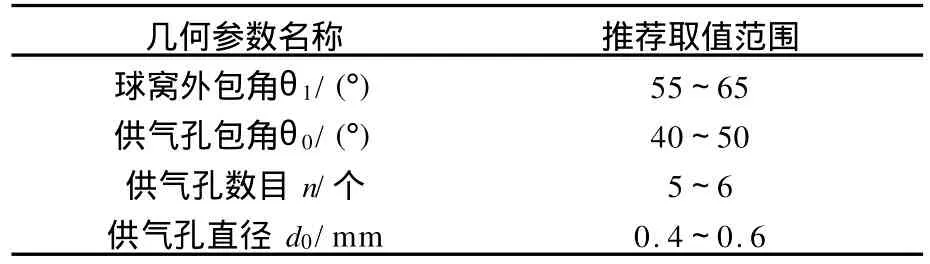
表2 闭式气体球轴承的推荐设计参数Table 2 Recommended parameters of spherical gas bearing

在仅考虑轴承静特性时,几何参数的设计过程如下:除轴承半径外,其他参数在表2推荐范围内选择,承载力、供气压力范围以及气体参数等由工作要求指定,剩下的几何参数(轴承半径)可用试算的方法确定。先指定一个较小的轴承半径,通过编制的程序算出对应的承载力特性,如果承载力特性不符合工作要求,则逐步增加轴承半径直至满足工作要求为止。

3 结论

(1)对轴承承载力特性影响较大的参数是球窝外包角和供气孔数,随着球窝外包角和供气孔数的增加,轴承承载力明显增大。

(2)对流量特性影响较大的参数是供气孔数和供气孔直径,随着供气孔数和供气孔直径的增加,气体耗气量明显增大。

(3)对静刚度影响较大的参数是球窝外包角、供气孔包角以及供气孔直径。当球窝外包角从25°增至65°时,最大静刚度显著上升;当球窝外包角超过65°时,随着外包角的增加,轴承在工作起浮高度5～50μm下的静刚度反而下降。当供气孔包角从10°增至40°时,轴承的最大静刚度随之增加至近似最大,当供气孔包角继续增加时,轴承的静刚度反而下降。随着供气孔直径的增加,工作起浮高度范围内轴承的静刚度明显下降。

(4)在仅考虑轴承静特性的情况下,为使轴承具有尽可能好的综合性能,推荐环面节流闭式气体球轴承的几何参数的取值范围为:球窝外包角55°～65°,供气孔包角40°～50°,供气孔数5～6,供气孔直径0.4～0.6 mm。

[1] 林来兴.卫星姿态控制系统半物理仿真实验和多转台仿真方法[J].航天控制,1993,11(4):73-80.

[2] 李季苏,牟小刚,张锦江.卫星控制系统全物理仿真[J].航天控制,2004,22(2):20-26.

[3] 查世红,梅涛.6自由度模拟卫星静压气浮轴承数值计算方法[J].机器人,2009,31(6):561-567.

[4] 解鹏,金光,张雷,等.小孔节流方式对静压气体球轴承工作特性的影响[J].润滑与密封,2010,35(3):77-80.

[5] 许剑,杨庆俊,包钢,等.多自由度气浮仿真试验台的研究与发展[J].航天控制,2009,27(6):96-101.

[6] 王祖温,郭良斌,包钢,等.单节流孔静压球面气体轴承动态特性的有限元分析[J].摩擦学学报,2003,23(5):416-420.

[7] 任迪,杨庆俊,王祖温,等.静压气体球轴承承载力的三维计算方法[J].大连海事大学学报,2008,34(2):79-82.

[8] 刘暾,刘育华,陈世杰.静压气体润滑[M].哈尔滨:哈尔滨工业大学出版社,1990:100-103.

[9] 郭良斌,王祖温,包钢,等.新型环面节流静压气体球轴承压力分布的有限元计算[J].摩擦学学报,2004,24(6):531-535.