矩阵方程组中心对称最小二乘解的迭代算法
(福建工程学院 软件学院,福建 福州 350003)
0 引言与引理

定义1 若矩阵X=(xij)n×n∈Rn×n的元素满足xij=xn+1-i,n+1-j(i,j=1,2,…,n),则称X为中心对称矩阵.全体n阶中心对称矩阵的集合记为CSRn×n.
本文讨论矩阵方程组
AiXBi+CiXDi=Fi(i=1,2)
(1)
的下列问题:
问题I 给定Ai,Bi,Ci,Di,Fi∈Rn×n(i=1,2),求X∈CSRn×n,使得
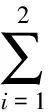


矩阵方程组特殊解的求解问题在光子光谱学、结构动力学和自动控制理论等领域都有重要应用.线性矩阵方程组的求解问题是数值代数方面的重要部分,比较成熟的算法[1-6]多种多样.本文借鉴共轭梯度法的思想,建立了一种变形共轭梯度法.解决了方程组(1)的中心对称最小二乘解及最佳逼近矩阵的计算问题.当方程组(1)有中心对称解时,求其中心对称最小二乘解等同于求中心对称解.
引理1 设A∈Rn×n,则A∈CSRn×n的充分必要条件是SAS=A.
引进记号:gi(X)=AiXBi+CiXDi(i=1,2).
定理1 求解问题I等价于求矩阵方程
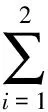
(2)
的中心对称解,且矩阵方程(2)一定有中心对称解,其中
证当X∈CSRn×n时,由引理1知X=SXS.因此,求X∈CSRn×n使得
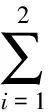
等价于求X∈CSRn×n使得
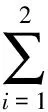
(3)
下面证明求解极小值问题(3)等价于求解矩阵方程(2).考虑矩阵方程组
{A1XB1+C1XD1=F1,A1SXSB1+C1SXSD1=F1
A2XB2+C2XD2=F2,A2SXSB2+C2SXSD2=F2
(4)
将矩阵方程组(4)按行拉直可得线性方程组
(5)
易见,求线性方程组(5)的最小二乘解等价于求矩阵方程组(4)的最小二乘解,即求极小值问题(3)的解.线性方程组(5)的正规方程组为
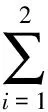
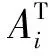
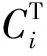
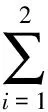
(6)
将线性方程组(6)还原即得矩阵方程(2).

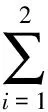
(7)
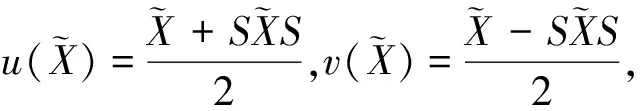
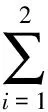
1 求解问题I的迭代算法
为了讨论方便,引进记号
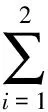
下面建立求矩阵方程(2)的中心对称解,即求解问题I的迭代算法(算法1).
第1步: 任取初始矩阵X0∈CSRn×n,计算
R0=H-f(X0),P0=f(R0).输值k:=0
第2步: 如果Rk=O,停止;否则,输值k:=k+1;

第4步: 转向第2步.
根据引理1,采用数学归纳法可以证明,当初始矩阵X0∈CSRn×n时,由算法1得到的矩阵Xk∈CSRn×n(k=1,2,3,…).由矩阵内积运算的交换律,容易证明下面结论.
引理2 设矩阵X,Y∈Rn×n,则[f(X),Y]=[X,f(Y)].
定理2 如果X*是问题I的解,那么对任意初始矩阵X0∈CSRn×n,由算法1得到的矩阵Xi,Ri和Pi满足
[Pi,X*-Xi]=‖Ri‖2(i=0,1,2,…)
(8)
证采用数学归纳法.对于i=0,由引理2可得
[P0,X*-X0]=[f(R0),X*-X0]=
[R0,f(X*-X0)]=[R0,H-f(X0)]=‖R0‖2.
假定i=s时(8)式成立,则当i=s+1时,有
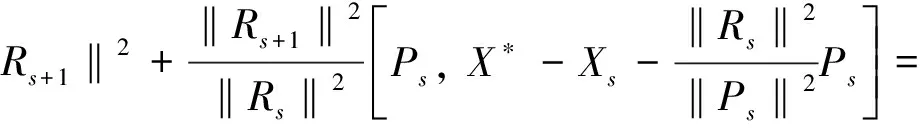

即(8)式也成立.由数学归纳法原理知,结论成立.证毕
推论1 若Ri≠O,则Pi≠O(i=0,1,2,…),从而算法1不会中断.
定理3 若存在正整数k,使得Ri≠O(i=0,1,…,k),则由算法1得到的Ri和Pi满足
[Ri,Rj]=0,[Pi,Pj]=0 (i≠j;i,j=0,1,…,k)
(9)
证根据矩阵内积运算的交换律,只需对0≤i 第1步: 证明[Ri,Ri+1]=0,[Pi,Pi+1]=0 (i=0,1,…,k-1).采用数学归纳法.当i=0时,有 假定对i 根据数学归纳法原理,对i=0,1,…,k-1,都有[Ri,Ri+1]=0,[Pi,Pi+1]=0. 第2步: 假定0≤i 根据数学归纳法原理,(9)式成立.证毕 推论2 对任意初始矩阵X0∈CSRn×n,问题I的解可在有限步迭代计算后得到. 事实上,在有限维矩阵空间Rn×n中,矩阵组R0,R1,R2,…两两正交,必定存在正整数k≤n2,使得Rk=0.但是,由于计算过程中舍入误差的影响,算法1不一定能够在有限步迭代计算后得到问题I的精确解,因此只能把它作为迭代算法使用. 引理3 设矩阵A∈Rm×n,列向量b∈Rm,线性方程组Ax=b有解,则极小范数解x*=A+b∈R(AT),且R(AT)中只有Ax=b的一个解.这里A+表示A的Moore-Penrose逆. 定义2 对于列向量x∈Rnm,定义n×m矩阵 mat(x)=[x(1:m),x(m+1:2m),…,x((n-1)m+1:nm)]T 其中x(i:j)表示向量x中第i个分量到第j个分量构成的列向量. 若取初始矩阵X0=f(Y0)(任意Y0∈CSRn×n),可以验证,由算法1得到的矩阵Xk,Rk,Pk∈CSRn×n(k=0,1,2,…),由算法1中Xk的表达式可导出 Xk=f(Yk)(Yk∈CSRn×n) (10) 记 将矩阵方程(2)按行拉直得到线性方程组 (11) (12) 综上所述,可得下面的结论. 定理4 问题I的解存在,不考虑舍入误差时,对任意的初始矩阵X0∈CSRn×n,由算法1经有限步迭代计算可得到问题I的解;若取初始矩阵X0=f(W)(任意W∈CSRn×n)由算法1得到的解X*是问题I的极小范数解,其表达式由(12)式给出. 因为上述等式右端两个矩阵的内积为零,所以 当X∈SE时,改写矩阵方程(2)为 令 例1 用算法1求问题I的极小范数解和问题II的解,其中 1)选取初始矩阵X0=O,终止准则‖Rk‖<10-9,求得 [‖A1X2B1+C1X2D1-F1‖2+‖A2X2B2+C2X2D2-F2‖2]1/2=29.5041. 易见,矩阵方程组AiXBi+CiXDi=Fi(i=1,2)无中心对称解,矩阵X2是其极小范数中心对称最小二乘解. 例2 用算法1求(1)的极小范数中心对称解,其中矩阵Ai,Bi,Ci,Di同例1,而 选取初始矩阵X0=O,求得 [‖A1X3B1+C1X3D1-F1‖2+‖A2X3B2+C2X3D2-F2‖2]1/2=3.0611×10-13. 易见,矩阵方程组AiXBi+CiXDi=Fi(i=1,2)有中心对称解,矩阵X3是其极小范数中心对称解. [1]姚健康.求解相容的矩阵方程组A1XB1=D1,A2XB2=D2的一种迭代法[J].南京师范大学学报:自然科学版,2001,24(1): 6-10. [2]彭卓华,胡锡炎,张磊.矩阵方程A1X1B1+A2X2B2+…+AlXlBl=C的中心对称解及其最佳逼近[J].数学物理学报,2009,29A(1):193-207. [3]张新东,张知难.矩阵方程AX=B的双反对称最佳逼近解[J].应用数学学报,2009,32(5):810-818. [4]盛兴平,苏友峰,陈果良.矩阵ATXB+BTXTA=D的极小范数最小二乘解的迭代解法[J].高等学校计算数学学报,2008,30(4):352-361. [5]戴华.对称正交对称矩阵反问题的最小二乘解[J].计算数学,2003,25(1):59-66. [6]袁飞,张凯院.矩阵方程AXB+CXTD=F自反最小二乘解的迭代算法[J].数值计算与计算机应用,2009,30(3):195-201.
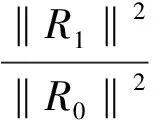



2 问题II的解
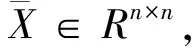



3 数值算例