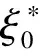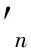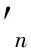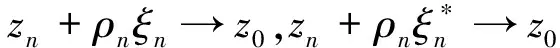分担值与正规族

,

(1.江苏省盱眙中学 数学组,江苏 淮安 211700;2.电子科技大学 数学学院,四川 成都 610054)

0 引言

1969年,Drasin D[1]证明了如下结果:

定理A[1]设F为区域D上的一族解析函数,a≠0,b为常数,n≥3为一正整数,如果对任意的f∈F,f′(z)-afn(z)≠b则F在D上正规.

上述定理是由Hayman W K[2]在1959年所提出的著名猜想.1991年,陈怀惠和方明亮[3]证明了定理A在n=2的时候也成立,对于亚纯函数,陈怀惠和方明亮[4]证明了如下定理:

定理B 设F为区域D上的一族亚纯函数,a≠0,b为常数,n≥3为一正整数,如果对任意的f∈F,f′(z)-afn(z)≠b则F在D上正规.

对于定理B,在n=2的时候并不成立,如

问题1.相应于定理B,在n=2的时候,我们是否可以从分担值的角度重新考虑呢?

相应于问题1,从分担值的角度出发,本文证明了

定理1 设F为区域D上的一族亚纯函数,a(z)≠0为D上的一解析函数,b为常数.如果对F中的任意两个函数f(z)和g(z),在D上f′(z)-a(z)f2(z)和g′(z)-a(z)g2(z)都以b为公共值,且f(z)和g(z)的所有极点重级≥3,则F在D上正规.

1 引理

为证明本文的定理,我们需要以下引理 .

引理1[5](Zalcman-Pang引理)设F为区域D⊂C上的一族亚纯函数,k为一个正整数,如果对任意的f∈F,f的零点重级≥k,那么对于任意的-1≤α

(a)点列{zn},zn∈D,zn→z0;

(b)函数列{fn},fn∈F;

其中收敛是按球面距离内闭一致收敛,且g(ξ)为复平面上的非常数亚纯函数,满足g*(ξ)≤g*(0)=kA+1.

注1 1)以色列数学家Zalcman[6]证明了α=0 的情形;1988年,庞学诚[7]证明了-1<α<1 的情形,这两种情况对零点不用作任何要求.1995年,庞学诚、Zalcman[8]又证明了-1<α≤k的情形.

2)当f(z)为复平面上的亚纯函数(整函数),如果f(z)的球面导数有界,则它的极至多为2(多为1).

引理2[9]设g(z)为复平面上的有限极超越亚纯函数,p为不恒为零的多项式.如果g(z)的所有零点重级≥k+1,则g(k)(z)-p有无穷多零点.

其中b≠0,c为常数,且若g(z)所有零点重级≥k+1,则

其中r,δ,α,β是常数满足αr≠0,|β|+|δ|≠0.

引理4 设g(z)为复平面上的有理函数,b≠0为一常数.如果g(z)所有零点重级≥3,则g′(z)=b至少有一解.

证明假设在复平面上g′(z)≠b,下面分两种情况讨论

1)g(z)是一个多项式,则g′(z)=b+c其中c≠0是一常数.因此

g(z)=(b+c)z+d

其中d≠0是一常数,这与g(z)零点重级≥3矛盾.

2)g(z)为一个非多项式的有理函数,则根据引理3由g′(z)≠b有

(1)

其中d≠0,c是常数.假设g(z0)=0.因为g(z)零点重级≥3,我们有

(2)

(3)

即有

这与d≠0,c≠0矛盾.

2 定理1的证明

(4)

按球面距离内闭一致收敛,且g(ξ)是复平面上的非常数的亚纯函数,g(ξ)的极≤2,g(ξ)的零点重数≥3.

由(4)我们有

按球面距离内闭一致收敛.

其中

由Hurwitze定理可知存在

使得对于充分大的n有

由题设对于F中的任意两个函数f(z)和g(z),在D上f′(z)-a(z)f2(z)和g′(z)-a(z)g2(z)都以b为公共值,则对任意的正整数m有

因此

以下证明没有这样的有理函数的存在,分两种情况讨论.

1)g(ξ)为一多项式.则-g′(ξ)-a(z0)=A(ξ-ξ0)l其中A为非零常数,l≥2为一个正整数.这时g”(ξ)=-Al(ξ-ξ0)l-1只有唯一零点ξ0,注意到g(ξ)零点重级≥3得到g(ξ0)=0;g′(ξ0)=0.这与-g′(ξ0)-a(z0)=0矛盾.

2)g(ξ)为非多项式的有理函数.g(ξ)无重级级点,则我们可以设

(5)

其中A≠0为常数,s≥1,t≥1为正整数,记m=m1+m2+…ms.由(5)知

其中

h(ξ)=(m-t)ξs+t-1+as+t-2ξs+t-2+…a0,

p1(ξ)=A(ξ-ξ1)m1-1(ξ-ξ2)m2-1…(ξ-ξs)ms-1h(ξ),

q1(ξ)=(ξ-η1)2…(ξ-η2)2(ξ-ηt)2,

是多项式.这与-g′(ξ)-a(z0)只有一唯一的零点矛盾.

[1]Drasin D.Normal families and nevanlinna theory[J].Acta Mathematic scientia,1969,122:231-263.

[2]Hayman W K.Research problem in function theory[M].Athlone press of university of London.1967:122-128.

[3]Chen H H,Fang M L.On a theorem of Drasin[J].Advance in Mathematics,1991,201:504-541.

[4]Chen H H,Fang M L.On the value distribution of fnf′[J].Sci China 1995,A(38):789-798.

[5]Yang L.Value distribution theory[M].Science Press,Berlin,1993:203-208.

[6]Zalcman L.A heuristic principle in complex function theory[J].Amer Math Monthly,1975,82:813-817.

[7]Pang X C.Normality conditions for differential polynomials[J].Kexue Tongbao,1988,33(22):1690-1693.

[8]Pang X C,Zalcman L.Normal families and shared values[J].Bull London Math.Soc,1995,18:437-450.

[9]Huang X J,Gu Y X.Normal families of meromorphic functions with multiple zeros and poles[J].Journal of Mathematical Analysis and Applications,2004,29(5):611-619.

[10]Wang Y F,Fang M L.Picard values and normal families of meromorphic function with multiple zeros[J].Acta Mathematica Scientia,1998,14(5):17-26.