生长曲线的拟合方法及营养评价界值点的选择

宗心南 李 辉

生长曲线是研究生长发育的一个重要内容，是儿童生长及营养评价的重要工具，是加强和巩固生长监测地位，促进和保障生长评价规范化、标准化及制度化的关键。现场调查获得的数据年龄分组较粗，百分位曲线图不够平滑，使用不够方便、准确，于是研究人员对百分位曲线进行修匀平滑，并在方法学上取得较大进步，诸如JPA2模型、Count模型、Kernel法、Lowess法、分段多项式及三次样条函数等[1～4]。但由于体重等偏态分布数据不易获得准确的标准差单位(SDS或Z分)曲线图，为此，美国和荷兰等[5,6]采用分别计算上半部和下半部标准差的方法。近年来，将偏态数据正态转换后再行曲线拟合的方法逐渐被接受，如Box-Cox正态性、Box-Cox幂指数、Box-Coxt和Johnson's SU等分布转换[1,4]，并逐渐形成以LMS法为基础的规范化的曲线拟合方法。在借助生长曲线进行生长与营养评价、临床医学诊断时，选择抑或制定一个合理的界值点(cut-off point)也是十分重要的技术环节。

1 生长曲线拟合方法

平滑技术和分布转换是生长曲线拟合的两大理论问题。三次样条函数和分段多项式是目前最常用的曲线平滑技术。鉴于偏态分布资料无法直接获得准确的标准差单位曲线，美国国家健康统计中心(NCHS)采用分别计算上半部和下半部标准差的方法[5]，而分布转换却能解决上述问题，将原始数据正态转换后再做平滑处理不仅可以获得合理的Z分曲线，极端(或边际)曲线估计亦更为精确[7]，目前常用的转换有Box-Cox正态转换和Box-Cox 幂指数转换。

1.1 LMS法 LMS法[8，9]是用中位数(M)，变异系数(S)及将资料转换成对称分布(接近正态)所需的度量偏度的Box-Cox转换幂(L)描述资料在年龄(或身高)上的分布，采用三次样条函数对L、M和S 3条曲线进行拟合，通过惩罚似然法对其选择并使其达到光滑。该法融合了Box-Cox正态转换和三次样条平滑技术，强调曲线的形状由L、M和S 3个参数决定，可根据式1计算任意百分位或Z分曲线值。

C100α(t)=M(t)[1+L(t)S(t)zα]1/L(t)(式1)

其中C100α(t)是年龄为t时的第100α百分位曲线的对应值，zα是尾部面积为1-α时的正态离差(如α=0.97对应于P97，zα=1.88)，L(t)，M(t)和S(t)是年龄为t时所对应的每条曲线的值。

LMS法不仅可处理资料偏态分布问题，估计边际百分位数也优于简单的“排序和计数”法[7]，而且利用L、M和S亦能计算个体测量值的Z分值(式2)。

其中Measurement 是儿童体格测量值(如身高和体重等)，L(t)，M(t)和S(t)是年龄为t时平滑曲线的对应值。当样本量较小时， L值受“极端值”影响较大[8]。实际应用LMS法拟合数据时，年龄是否分组主要由研究设计决定，LMS法并不排斥年龄分组，只是分组节点的选择是人为的，理论上会对结果产生影响[9]。

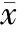
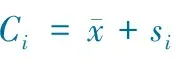
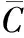
当λ≠0时，Ci=[Hi/H-1]/λ

当λ=0时，Ci=log(Hi/H) (式4)

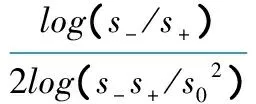
1.3 LMSP法 Box-Cox 幂指数分布(BCPE)是将非正态资料转换成正态分布的一种数学模型，除了涉及前述修正LMS法提到的μ、σ(CV)和λ 3个参数又增加了τ(与峰度相关的幂指数)参数[13]。当λ=1，τ=2时模型简化为正态分布；当λ≠1，τ=2时简化为Box-Cox正态转换(即LMS法的分布)[1]。以衡量模型拟合优度标准的最小Akaike信息准则(AIC)和GAIC(generalized AIC)选择数据转换所需的参数自由度，以虫行图[14]和Q检验[15]评价模型优劣。采用三次样条函数(或其他方法)对上述4个参数平滑处理，以最大似然法选择光滑参数[13]。将上述采用BCPE转换和三次样条函数进行曲线拟合的方法称为LMSP法。WHO统计咨询组建议当BCPE转换比Box-Cox正态转换对生长曲线精度估计有显著提高时应使用前者[4]。LMSP法是在LMS法基础上增加了与峰度有关的τ参数，进一步解决了数据峰态分布问题，扩大了模型的应用范围，但是由于峰度较偏度对数据分布影响小[9,12]，两者拟合结果非常近似，所以两者都是目前构建生长曲线最常用的方法。

1.4 其他方法

1.4.1 补偿返还 婴幼儿因站立困难无法准确测量立位身高而测量卧位身长。中国儿童体格测量习惯采取<3岁测量身长，≥3岁测量身高。美国则采用<2岁测量身长，≥2岁测量身高。WHO新标准在制定中采用<2岁测量身长，≥2岁测量身高，2～3岁同时测量身长和身高，由此证实卧位身长比立位身高测量数据多0.7 cm。既往制定生长曲线时是将身长与身高视为等同变量，但考虑到两者测量属性并不相同，若直接合并，则平滑后的曲线在接口处(如2或3岁)会出现较大偏差。近年来在建立年龄的身高模型时，为了在整个年龄段用单一模型拟合连续的生长曲线，常采用偏量(0.7或0.8 cm)补偿返还[1，12，16]。步骤如下：将身高加0.7 cm后与身长合并，然后在整个年龄范围构建单一模型，结果产生后将>2或>3岁的身长中位数减0.7 cm 转换成身高，CV亦作相应转换，最后根据式1重新计算任意百分位或Z分曲线数值，婴幼儿期身长模型拟合数据不变。但在构建身长或身高的体重时，补偿返还过程与前述不尽相同，将身高加0.7 cm与身长合并，在整个身长范围用单一模型拟合身长的体重，由于该模型中身长为自变量，故数据拟合后，可直接截取45～105 cm为身长的体重，将拟合后身长减去0.7 cm可转换为身高，然后截取身高的体重为65～125 cm(对应的身长为65.7～125.7 cm)。

1.4.2 补偿独立 BMI是反映儿童营养状况的重要指标，其与身高的平方成反比，因此拟合BMI曲线时不能采取简单的补偿返还法[1，16]，取而代之的是补偿独立法[1，17]，即采取身长BMI 和身高BMI分别独立拟合的方法：将身高加0.7 cm计算身长BMI，然后在整个年龄段拟合身长BMI，曲线拟合后可根据需要截取0～2岁或0～3岁BMI；类似方法，将身长减0.7 cm计算身高BMI，亦在整个年龄段拟合身高BMI，模型产生后可按要求截取2～18岁或3～18岁BMI为参照标准。选择分别独立拟合以及在整个年龄段建立模型，是由研究设计及BMI自身特征决定，同时更大程度地减少了边缘效应[1，4]。

1.4.3 边缘效应 边缘效应是指在生长曲线模型构建时靠近年龄边缘(或两端)部分，其估计精度会降低。效应大小与曲线形状、光滑参数、年龄分组及样本量等有关。WHO通过模拟试验发现增大初生组样本量(如原样本的4倍)及适当的年龄扩展会缩小边缘效应。以WHO新标准为例，该标准截取为0～60个月，但曲线拟合时采用了所有收集的0～71个月数据以减少右边缘效应。为使左边缘效应最小化，在设计时增加年龄下限的样本量来增强曲线稳定性[4]。

1.4.4 年龄扩展 通常在使用三次样条函数之前，对生长模型接近零年龄处进行年龄幂转换来扩展年龄[1，4]，目的是提高拟合优度，降低左边缘效应。构建模型时，增加足够的自由度可以使婴儿期生长曲线拟合得很好，但却使较大年龄曲线不够光滑，解决的办法是当生长速率较大时采用幂转换扩展年龄，当速率较小时压缩年龄。因此，曲线拟合时通常先选择一个简单模型(自由度固定)，根据全局偏差改变量来确定合适的幂指数，可在0.05～1以每0.05单位试验。年龄扩展对拟合BMI曲线非常重要，但对身高和体重等可不进行幂转换。

1.4.5 拟合优度 拟合效果评价是生长曲线研究中的重要环节。

其一：分性别、年龄组比较拟合值与实测值在经验百分位之间差值，该指标从专业实践的角度来判断、认识研究的合理性和可接受程度。

其二：通过构造χ2统计量[7，16]，从统计概率角度考察数据拟合后的理论分布与实际分布是否一致，具体如下：首先利用式2将每年龄组原始数据转换成Z分，然后计算个体Z分落在P3、P10、P25、P50、P75、P90和P97(对应的Z分依次为-1.88，-1.28，-0.67，0，0.67，1.28和1.88)百分位曲线区间的比例，从而能比较期望比例与实际比例的差异是否具有统计学意义。

2 界值点选择方法

界值点是指机体由一种状态转化为另一种状态的关键条件，包括诊断界值点和筛查界值点。诊断界值点与“疾病”相联系，获取该界值点有两个假设[18]：①有病者给予治疗，无病者不予治疗；②治疗与不治疗由试验结果确定。筛查界值点与“异常”相联系，获取该界点也有两个假设：①根据试验结果确定对象是否被重点关注；②“异常”并不一定有病，临床确诊应结合其他指标。身高和体重是两项最简单的、能用于评估居民营养状况的人体测量指标，WHO将身高和体重及其相关指标作为实施营养干预计划及评估干预效果的依据[19]。近年来，随着对人体测量学的深入研究，这些指标应用范围不断扩大，各个国家或地区结合实际已制定或选用了儿童生长参照标准，并根据生长及营养状况确定了适宜的界值点。目前，儿童体格生长指标界值点多是以人群为基础的统计界值，更多地是从营养监测、卫生经济学和公共卫生理论角度考虑，这种筛查界值点并不是一个独立的诊断标准，临床应用时要与其他指标及临床症状或体征相结合。

2.1 百分位法或评分标准差(SDS)法 百分位法或SDS法是指男、女儿童均采用相同的百分位数或SDS作为界值点对生长或营养状况进行分类，该法适用于多种指标，有较强的公共卫生理论基础。美国[12，20]将P5和P95分别作为儿童生长监测的界值点，该界值点并没有直接考虑其与生化指标或疾病发生或死亡的关系，而是将重点放在从儿童保健和公共卫生角度加强生长监测和保障儿童健康成长。多数欧洲国家将P3和P97作为筛查和评估儿童生长水平的界值点[21，22]。英国学者Cole[23]和Wright等[24]建议用一套9线百分位曲线图替代传统的7线图更有利于监测儿童生长与营养状况，该9线曲线将-2.67s～2.67s以0.67s等距划分，分别对应于P0.4、P2、P9、P25、P50、P75、P91、P98和P99.6，认为儿童身高低于P0.4(4/1 000)应给予及时治疗，在P0.4～P2应重点观察，高于P2可能无严重问题[7，23]。WHO推荐将低于-2s或高于2s作为儿童营养不良或肥胖的分类界值点[19，25，26]，随着LMS法被广泛应用，SDS法将会越来越受到重视。

2.2 与成人界值点接轨法 与成人界值点接轨法是将男、女儿童BMI曲线在18岁时通过成人低体重、超重和肥胖界值点所对应的百分位曲线定义为适宜界值点，目前该法仅适于BMI指标。由于BMI性别差异明显，当BMI曲线通过成人界值点时对应的百分位曲线可能是不同的。1997年，国际肥胖工作组(IOTF)在都柏林会议上，接受将BMI作为成人及儿童肥胖评价指标，并正式提出将18岁时通过25和30 kg·m-2两点的相应BMI百分位曲线作为不同性别-年龄别超重和肥胖界值点[27]。Cole等[28，29]汇集6个国家和地区(巴西、英国、中国香港、荷兰、新加坡和美国)横断面调查生长数据，采用LMS法建立BMI参照曲线，按照IOTF的建议，将18岁时BMI值通过成人低体重、超重及肥胖的诊断界值点，提出国际上统一的儿童营养分类BMI参照标准。2007年，WHO推出了以美国调查数据为蓝本、采用LMSP法建立的5～19岁BMI参照值，该参照值在19岁时，男、女儿童BMI值+1s时分别为25.4和25.0 kg·m-2，+2s时均为29.7 kg·m-2，被建议作为儿童超重和肥胖筛查界值点[25]。

2.3 中位数百分比法 中位数百分比法是以某指标中位数为基础，按一定的百分比上下浮动得到不同的生长或营养分类标准，最常用于身长(身高)的体重，也见于身高和体重等。该法源于将欧美等国家的参照值做适当修改可用于监测发展中国家儿童营养状况，关键在于首先要选择适宜参照值中位数并将其定义为100%，然后探索可接受的浮动百分比。20世纪80年代，WHO采用该法建立了身高的体重营养分类标准提供给有关国家或地区使用，制定过程为：将NCHS/WHO身高的体重中位数定义为100%，以中位数(100%)±10%为正常范围，低于90%中位数为低体重，低于80%为营养不良，高于110%为超重，高于120%为肥胖。该法基于各民族间某些指标中位数差异较小，制定过程简易，易于实施，可进行等级评价，有较好的区分度。但从专业角度看，该法与生长规律并不十分吻合，尤其是进入青春期，这种线性模式并不能充分反映人群变异度，随着各个国家或地区自己民族的生长参照值的建立，其应用会受到挑战。

2.4 ROC曲线法 接受者工作特征(ROC)曲线法是目前选择界值点最可靠的方法，前提是必需有“金指标”，在儿童生长领域由于获取“金指标”难度大，致使该法只在小样本调查中应用或辅助验证预先选定的界值点的灵敏度和特异度。Lusted于1971年率先将该法用于医学决策，克服既往灵敏度、特异度及其相关指标的缺陷，此后，该法成为最有价值的描述与比较诊断试验的工具[30]。最简单的界值点选择方法是取ROC曲线“左上方”[31]或“距离最短”[32]对应的截断点，但在确定界值点过程中，还应综合考虑疾病或健康状态的特征、诊断或筛检目的和卫生经济学效果。儿童生长是一个复杂动态变化的过程，身体测量及其他生理生化指标变动较大，儿童期营养相关性疾病比成人少或还没呈现显性病变，不易获得“金指标”，给确定界值点带来很大挑战。Alonzo等[33]利用儿童BMIZ分预测成人肥胖的纵向研究或许能为选择界值点提供另一条途径。

2.5 人群验证法 人群验证法是将已选定的某个(或若干)界值点用于某人群营养评价，强调结果的现实性和可接受性，是一种辅助选择界值点的方法，不具有独立意义。交叉验证和回代验证是常用的两条途径，前者选用参照样本以外的人群，对部分生理和生化指标进行交叉验证，以衡量界值点的灵敏度和特异度；后者是将已选定的界值点回代入参照样本或以外的不同人群中，衡量不同人群的适用性。儿童青少年是全人群中相对最健康的一个群体，不像婴幼儿或成人那样，以死亡率、相关疾病患病率或危险因素等作为前瞻性的验证指标，所以对生长标准[34]或界值点[35，36]进行人群验证就显得尤为重要，也为其进一步推广应用提供科学依据。

[1]WHO Multicenter Growth Reference Study Group.WHO child growth standards: length/height-for-age, weight-for-age, weight-for-length, weight-for-height and body mass index-for-age: Methods and development.Geneva: World Health Organization, 2006.http://www.who.int/childgrowth/standards/en/

[2]Li H, Leung SS, Lam PK, et al.Height and weight percentile curves of Beijing children and adolescents 0-18 years, 1995.Ann Hum Biol, 1999, 26(5):457- 471

[3]Chen CS(陈长生),Xu YY,Xia JL,et al.中国香港地区0-7岁儿童生长曲线的非参数模型构建.Chin J Prev Med(中华预防医学杂志), 2000, 34(1): 47-49

[4]Borghi E, de Onis M, Garza C, et al.Construction of the World Health Organization child growth standards: selection of methods for attained growth curves.Stat Med, 2006, 25(2): 247-265

[5]Dibley MJ, Goldsby JB, Staehling NW,et al.Development of normalized curves for the international growth reference: historical and technical considerations.Am J Clin Nutr,1987, 46(5): 736-748

[6]Gerver WJM, de Bruin R.Paediatric morphometrics: a reference manual.Utrecht, The Netherlands: Wetenschappelijke Uitgeverij Bunge, 1996: 61-63

[7]Freeman JV, Cole TJ, Chinn S, et al.Cross sectional stature and weight reference curves for the UK, 1990.Arch Dis Child , 1995, 73(1): 17-24

[8]Cole TJ.Fitting smoothed centile curves to reference data.J Roy Statist Soc Ser A,1988, 151: 385-418

[9]Cole TJ, Green PJ.Smoothing reference centile curves: the LMS method and penalized likelihood.Stat Med, 1992, 11(10): 1305-1319

[10]Cole TJ.Using the LMS method to measure skewness in the NCHS and Dutch National height standards.Ann Hum Biol, 1989, 16(5): 407-419

[11]Cole TJ.The British, American NCHS, and Dutch weight standards compared using the LMS method.Am J Hum Biol, 1989, 1: 397-408

[12]Kuczmarski RJ, Ogden CL, Guo SS, et al.2000 CDC Growth Charts for the United States: methods and development.Vital Health Stat, 2002,(246):1-190

[13]Rigby RA, Stasinopoulos DM.Smooth centile curves for skew and kurtotic data modelled using the Box-Cox power exponential distribution.Stat Med, 2004, 23(19): 3053-3076

[14]van Buuren S, Fredriks M.Worm plot: a simple diagnostic device for modelling growth reference curves.Stat Med, 2001, 20(8):1259-1277

[15]Royston P, Wright EM.Goodness-of-fit statistics for age-speci-fic reference intervals.Stat Med, 2000, 19(21):2943-2962

[16]Capital Institute of Pediatrics(首都儿科研究所)，Coordinating Study Group of Nine Cities on the Physical Growth and Development of Children.Growth standardized values and curves based on weight, length/height and head circumference for Chinese children under 7 years of age.Chin J Pediatr(中华儿科杂志),2009, 47(3): 173-178

[17]Capital Institute of Pediatrics(首都儿科研究所)，Coordinating Study Group of Nine Cities on the Physical Growth and Development of Children.Growth standardized values and curves based on weight for length/height,body mass index for Chinese children under 7 years of age.Chin J Pediatr(中华儿科杂志),2009, 47(4): 281-285

[18]Dwyer AJ.In pursuit of a piece of the ROC.Radiology, 1996, 201(3): 621-625

[19]世界卫生组织, 编.吴熙增, 译.营养状况变化的测定.北京: 人民卫生出版社, 1986.8-29

[20]Must A, Dallal GE, Dietz WH.Reference data for obesity: 85th and 95th percentiles of body mass index (wt/ht2) and triceps skinfold thickness.Am J Clin Nutr, 1991, 53(4): 839-846

[21]Tanner J, Whitehouse R.Clinical longitudinal standards for height, weight, height velocity and weight velocity and stages of puberty.Arch Dis Child, 1976, 51(3): 170-179

[22]Gerver WJM, De Bruin R.Paediatric Morphometrics: a reference manual.Utrecht, Netherlands: Bunge, 1996.1-20

[23]Cole TJ.Do growth chart centiles need a face lift? BMJ, 1994, 308(6929):641-642

[24]Wright CM, Booth IW, Buckler JMH, et al.Growth reference charts for use in the United Kingdom.Arch Dis Child, 2002, 86(1): 11-14

[25]de Onis M, Onyango AW, Borghi E, et al.Development of a WHO growth reference for school-aged children and adolescents.Geneva: World Health Organization,2007.http://www.who.int/zh

[26]de Onis M, Onyango AW, Borghi E, et al.Comparison of the World Health Organization (WHO) child growth standards and the National Center for Health Statistics/WHO international growth reference: implications for child health programmes.Public Health Nutr, 2006, 9(7): 942-947

[27]Bellizzi MC, Dietz WH.Workshop on childhood obesity: summary of the discussion.Am J Clin Nutr, 1999, 70(1):173-175

[28]Cole TJ, Bellizzi MC, Flegal KM, et al.Establishing a standard definition for child overweight and obesity worldwide: international survey.BMJ, 2000, 320(7244): 1240-1243

[29]Cole TJ, Flegal KM, Nicholls D, et al.Body mass index cut offs to define thinness in children and adolescents: international survey.BMJ, 2007, 335(7612): 194

[30]Zhou XH, Obuchowski NA, McClish DK, 主编.宇传华, 译.诊断医学统计学.北京: 人民卫生出版社,2005.13-24

[31]金丕焕, 主编.医用统计方法.第2版.上海: 复旦大学出版社, 2003.428-431

[32]Zhou BF(周北凡),Wu YF,Li Y,et al.The cut-off point of waist circumference for identifying metabolic syndrome in Chinese adults.Chin J Cardiol(中华心血管病杂志),2005, 33(1): 81-85

[33]Alonzo TA, Pepe MS.Distribution-free ROC analysis using binary regression techniques.Biostatistics, 2002, 3(3): 421-432

[34]Onyango AW, de Onis M, Caroli M, et al.Field-testing the WHO child growth standards in four countries.J Nutr, 2007, 137(1):149-152

[35]Mei Z, Grummer-Strawn LM, Pietrobelli A, et al.Validity of body mass index compared with other body-composition screening indexes for the assessment of body fatness in children and adolescents.Am J Clin Nutr, 2002,75(6): 978-985

[36]Group of China Obesity Task Force(中国肥胖问题工作组).Body mass index reference norm for screening overweight and obesity in Chinese children and adolescents.Chin J Epidemiol(中华流行病学杂志),2004,25(2):97-102