高等数学中定积分应用部分的教学研究

齐 秀 丽

(绥化学院 数学与信息科学学院，黑龙江 绥化 152061)

1 引言

积分理论是高等数学教学中的重点部分，而整个积分理论(包括一元函数的定积分，多元函数的重积分、曲线积分、曲面积分)用于解决实际问题时所使用的思想方法均来自于微元法。因而，微元法成为积分理论应用部分的教学重点。

2 微元法分析

2.1 微元法思想下的定积分应用

对于曲边梯形面积的计算、变速直线运动路程的计算、变力做功的计算等问题，从数学角度来看，解决这些问题的方法、结果是相同的。抛开这些问题的实际背景，抽取出共同的数学过程，形成了定积分的概念。下面以“变速直线运动的路程”为例进行分析。

如果某个要求的量A依赖于定义在区间[a,b]上的函数f(x)，而且具有区间可加性，可以考虑利用定积分进行计算，如距离、功、面积、体积、质量等。不管是求曲边梯形的面积，还是求变速运动的物体经过的路程，总的思路都是先将所求问题从数量的角度进行划分，然后对细小的部分量进行近似求解，作出有限项的和，最后求极限。

用微元法的思想，通过定积分求A的步骤：

(1)由具体问题，选取积分变量x，并确定它的取值区间为[a,b]。

(2)在[a,b]上任取一个小区间，记为[x,x+dx]，并记在该区间上A的部分量为ΔA。如果ΔA能近似地表示为一个连续函数f(x)在x处的值与dx的乘积，即ΔA≈f(x)dx,记dA=f(x)dx,且ΔA-dA是一个比Δx高阶的无穷小量，则称dA为对应于所求量A的微元。

问题中，微元dA=f(x)dx的含义如下表所示。

f(x)表示的量dx表示的量f(x)dx表示的量∫baf(x)dx表示的量直线运动的速度时间间隔位移位移力距离功功电流强度时间间隔电量电量线密度长度质量质量面积长度体积体积……………………

2.2 三个重要公式的原理分析

2.2.1 直角坐标系下平面图形面积公式

设平面上四边形由两条曲线y=f1(x)、y=f2(x)，其中f1,f2为定义在[a,b]上的连续函数，且f2(x)≥f1(x),x∈[a,b]及直线x=b,x=a所围成，求其面积A。

分析：把四边形向x轴做投影，得到了x轴上的区间[a,b]。要求的四边形面积可以看做是分布在[a,b]上的整体量。该整体量满足微元法的两个条件。取x为积分变量，它的变化区间为[a,b]。设想把[a,b]分成若干个小区间，并把其中的代表性小区间记作[x,x+dx]，与这个小区间相对应的窄四边形的面积ΔA近似等于高为|f2(x)-f1(x)|dx，底为dx的窄矩形的面积|f2(x)-f1(x)|dx，从而得到面积元素dA，即dA=[f2(x)-f1(x)]dx，于是得到所求平面图形的面积为

2.2.2 极坐标系下平面图形面积公式

设曲线ρ=ρ(φ)(ρ(φ)∈c[α,β])与射线φ=α,φ=β围成一图形(称为曲边扇形，0≤ρ≤ρ(φ),α≤φ≤β以下简称曲边扇形)，求其面积A。

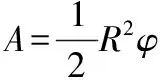
2.2.3 旋转体的体积

设旋转体是由平面上的曲边梯形0≤y≤f(x),a≤x≤b绕x轴旋转而成。

3 例题详解

3.1 定积分在求变力做功中的应用

从物理学知识知道，如果物体在受到恒力F(大小和方向均不变)的作用而作直线运动的过程中，当物体移动了距离S时，恒力F对物体相应的所做的功是W=FS。但如果其所受力F是变化的，则可以利用微元法的思想用定积分求变力所作的功。

例1：如图1所示，在地面下挖一圆柱形水池，底半径为5m，高为20m，其中灌满了水。求把所有的水抽到地面所作的功。

解：由于池中的水是被连续不断地抽到地面，被抽出的水可以被分割成不同的水层。而不同的水层与地面的距离不等，因而它们被抽出所作的功也不相等。将每一小薄层被抽出时需要的功定义为功微元，该问题符合微元法的条件。

在液面处取原点，竖直向下做x轴。从池内抽水时，池内液面逐渐降低，当由x处下降dx时，因dx很小，可近似地认为这“一层水”统统都提升了x，因而对这距离原点长度为x、厚度为dx的“水层”所作的功微元dW有近似计算公式

dW≈25πxdx(J)

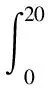
把水抽完时，池内的液面从0m降到20m，从而所求的功为

3.2 定积分在求液体静压力的应用

在这类问题中，总假设液体是静止的。物理学中关于压力的几个基本原理如下：

(1)面积为s的平板水平放置在液体中，在液面下深为h，则平板一侧所受液体的静压力为F=ρghs。

(2)密度均匀的薄板的一侧受液体的静压力，其受压部分的面积为s，受压部分的重心位于液体中的深度为h，则薄该侧所受液体静力为F=ρghs。

(3)密度均匀的物体的外侧受液体的静压力，其受压力部分的表面积为s，受压力部分的重心位于液体中的深度为h，则物体外所受液体的静压力为F=ρghs。

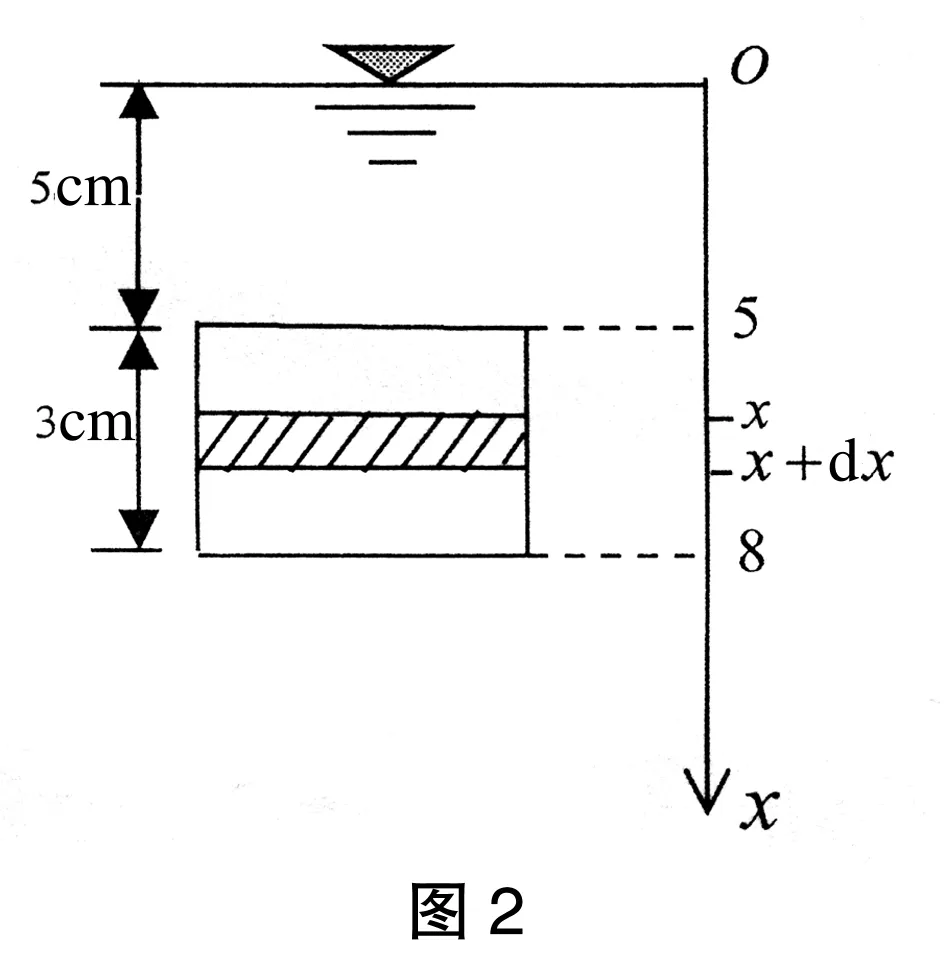
例2：如图2所示，一形状规则水下闸门的宽为4m，高为3m，其顶在水下5m，它垂直于水面放置。求它所受的水压力。

解：如图2建立坐标系。如果将闸门分成许多平行于液面的小条，闸门上所受的压力等于各窄条上所受压力的总和。当每一横条很窄，窄条上各点的深度变化不大，因而其各点处的压强，可用上方横线上的压强来近似计算，任取一窄条(图中阴影部分)，其压强可近似为1·x=x，小窄条的面积为ΔA=4dx，所以ΔP≈x·4dx。从而

另外公式中所用的函数f(x)均指相应区间上的单值连续函数。

[1]华东师范大学数学系.数学分析(上册)[M].北京：高等教育出版社,2001.

[2]李凯,周学君.关于两类定积分的求解方法[J].太原师范学院学报：自然科学版,2008，(4).

[3]同济大学应用数学系.高等数学(上册)[M].北京：高等教育出版社,2001.