矩阵秩的不同定义及其比较

王玉富

(郑州测绘学校，河南 郑州 450015)

传统的代数学中有两种定义矩阵的秩的方法. 一种是利用向量组的线性相关性来定义，即用矩阵的行向量(或列向量)组中极大无关组中向量的个数定义为矩阵的秩(第一定义)[1-6].由于许多管理类专业对向量组线性相关性的内容要求不高或根本不做要求，因而可以改用矩阵中不为零的子式的最高阶数来定义矩阵的秩(第二定义)[7-11].

这两个定义是完全等价的，把一个作为定义后另一个就可以作为定理使用. 第二定义貌似简单，绕开了向量的线性相关性，但却把问题复杂化了：从定义上无法理解“秩”是什么，利用定义来求矩阵的秩也是不现实的；即使算出来，也只是个抽象的数字，要想解释清楚“秩”，还必须再回头利用向量组(矩阵的行向量)的相关性来解释，或者通过初等变换变成阶梯型矩阵来计算.

本文将对该定义的方法及应用作进一步的探讨，并比较三种定义的优劣.

1 矩阵的初等变换与初等方阵

1.1 矩阵的初等变换

定义1 下面三种矩阵间的变换称为矩阵的初等行变换：

1)对调两行；

2)以非零常数乘某一行的所有元素；

3)把某一行所有元素的某一倍数加到另一行对应元素上去；

矩阵的初等行变换与线性方程组的等价变换相对应.

将定义1中的“行”换成“列”，就得到矩阵的初等列变换的定义. 初等行变换和初等列变换这3类(6种)矩阵间的变换统称为矩阵的初等变换.

定义2 如果矩阵A经过若干次初等变换变成矩阵B,则称矩阵A与B等价,记为A～B.

等价是矩阵间的一种关系，满足：

1)A～A(自身性)；

2)A～B,则B～A(对称性)

3) A～B, B～C则A～C(传递性).

结合行列式的性质，对于方阵，有：

定理1 如果一个方阵为奇异方阵(行列式的值为0)，则对其进行初等变换后仍然为奇异方阵；对非奇异方阵，无论进行什么样的(有限次)初等变换，都不能将其变成奇异方阵.

换句话说，等价方阵的行列式的值同时为0或同时不为0.

1.2 初等方阵

定义3 对单位矩阵E进行一次初等变换所得到的矩阵称为初等方阵.

1)对调单位矩阵E的第i行与第j行(或第i列与第j列)，得到的初等方阵记为P(i,j);

2)以非零常数k乘单位矩阵E的第i行(或第i行列)，得到的初等方阵记为P(i(k));

3) 单位矩阵E的第i行的每一个元素加上第j行相应元素的k倍(或第j列的每一个元素加上第i列相应元素的k倍，得到的初等方阵记为P(i,j(k)).

命题1 对矩阵A进行一次初等行变换，相当于用一个相应的初等方阵左乘矩阵A；对矩阵A进行一次初等列变换，相当于用一个相应的初等方阵右乘矩阵A.

命题2 初等方阵都是可逆的，其逆矩阵仍然是同类初等方阵：

P-1(i,j)=P(i,j)；P-1(i(k))=P(i(1/k));

P-1(i,j(k))=P(i,j(-k)).

1.3 阶梯型矩阵与矩阵的标准型

定义4 如果矩阵J的第s行的第一个非零元素为ast,对该矩阵的任一元素aij,当i>s且j≤t时，都有aij=0，则称J为阶梯型矩阵，如：

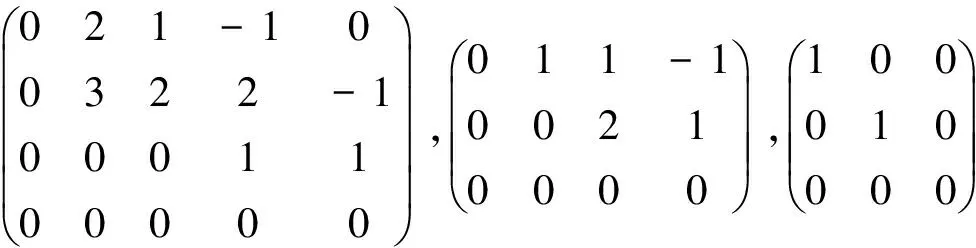
等，都是阶梯型矩阵. 零矩阵(元素全部为0的矩阵)也可以看作特殊的阶梯型矩阵.

命题3 任何一个矩阵总可以经过一系列初等变换变成一个阶梯型矩阵. 即任何一个矩阵A都等价于某一个阶梯型矩阵J.

显然，采用不同的初等变换所得到的阶梯型矩阵可能不相同,不过它们都可以通过进一步的初等变换变成“标准型”的形式.

定义5 如果矩阵A经过一系列初等变换变成:

的形式，其中左上角为一个r阶单位子块，其余元素全部为0,则称I为A的标准型.

定理2 两矩阵等价的充分必要条件是它们具有相同的标准型.

证明如果矩阵A和矩阵B具有相同的标准型I,且A～I,B～I,从而A～B，充分性得证.

如果矩阵A的标准型为I1,B的标准型为I2,而且I1≠I2,下面证明A不可能等价与B.

假设A～B，则存在一系列的初等变换能将A变成B，即存在一系列的初等方阵Pt,…,P2,P1和Qs,…,Q2,Q1使得:

B=Pt…P2P1AQ1Q2…Qs，

又由于A～I1,假设存在一系列的初等方阵Rk,…,R2,R1和Si,…,S2,S1使得:

A=Rk…R2R1I1Si…S2S1，

这样B=Pt…P2P1Rk…R2R1I1Si…S2S1Q1Q2…Qs

即B～I1；

同样A～I2

所以I1～I2

进而I1=I2

这与I1≠I2,矛盾，故当I1≠I2,时，A不等价于B.

推论1 一个矩阵的标准型是唯一的.

推论2 一个矩阵经初等变换化成阶梯型后非零行的个数是一个确定的数，等于其标准型中非零元素的个数.

2 矩阵的秩

2.1 矩阵的秩的定义(第三定义)

定义6 矩阵A经过初等变换所化成的阶梯型中非零行的个数称为矩阵A的秩.矩阵A的秩为r, 记为R(A)=r.特别，零矩阵O的秩R(O)=0.

该定义不仅便于理解，用该定义计算矩阵的秩也十分方便. 只要对矩阵进行初等变换变成阶梯型就能直接看出其秩了.

命题4 将矩阵A划去若干行得到矩阵B,则R(B)≤R(A).

2.2 矩阵的秩与子式的关系

定义7 在矩阵A中任取k行k列，位于这k行k列交叉处的k×k个元素按照它们原来的次序构成一个k阶行列式，称为矩阵A的一个k阶子式.

定理3 若矩阵A中有一个k阶子式不等于0,则R(A)≥k;若A的所有l阶子式都等于0,则R(A)

证明如果A中有一个k阶子式不等于零，则将这个子式所在的行对调到前k行,并对这k行进行初等行变换，可以变成一个阶梯型子块，该子块中不可能有一行全部为零，否则与原k阶子式不等于0矛盾，根据命题4,R(A)≥k；若A的所有l阶子式都等于0,则将A等价变成阶梯型后非零行的个数不可能大于或等于l,否则A中应至少有一个l阶子式不为零，所以R(A)

与定理3等价的说法是：

命题5 矩阵A的秩R(A)=r的充分必要条件是：A中至少有一个r阶子式不等于0,而所有r+1阶子式全部为0.

由此可见，矩阵A的秩就是A中不为零的子式的最高阶数(第二定义).

2.3 关于矩阵的秩为r的进一步解释

设A为m行n列矩阵，将A写成分块矩阵的形式：

这里A1=(a11,a12,…,a1n),A2=(a21,a22,…,a2n), …，Am=(am1,am2,…,amn), 都是1行n列的行向量.

1)若R(A)=m, 则无论对A进行什么样的初等行变换，都不可能将A的某一行变成O=(0,0,…,0)，亦即不可能存在一组不全为零的实数k1,k2…km,使:

k1A1+k2A2+…+kmAm=0.

我们说，当R(A)=m时，矩阵A的m行是独立的，或曰线性无关的.

2)若R(A)=m-1,可以利用初等行变换将A的某一行变成0,即存在一组不全为零的实数λ1,λ2,…,λm,使:

λ1A1+λ2A2+…+λmAm=0.

成立.这时，矩阵A的m行是不独立的或曰线性相关的， 矩阵A的某一行可以由其他行经线性运算得到. 但是，去掉某一个能用其他行线性运算得到的行后，剩余的m-1就独立(线性无关)了.

3)一般地，设R(A)=r

考虑矩阵A的转置矩阵AT，A中每一个子式都以转置的形式出现在AT中，故R(A)=R(AT)，亦AT中也有r行线性无关，但AT的行就是A的列.因而有下述命题：

命题6 矩阵A的秩等于其行向量(或列向量)组中独立的(线性无关的)向量的最大个数(第一定义).

至此证明了矩阵的秩的三个定义是完全等价的.

3 应用举例

几乎所有能够用相关性来证明关于矩阵秩的命题，利用第三定义都可以得到证明，例如一个重要命题:

R(AB)≤min{R(A),R(B)}

用第三定义结合初等变换来证明非常简单：

证明设R(A)=r，A的标准型为I. 这样存在一系列的初等方阵Pt,…,P2,P1和Qs,…,Q2,Q1使得:

A=Pt…P2P1IQ1Q2…Qs,

从而AB=Pt…P2P1IQ1Q2…QsB.

令Q1Q2…QsB=B1,

则B1～B,R(B1)=R(B) .

这样AB=Pt…P2P1(IB1),

故AB～IB1,R(AB)=R(IB1)，

其中I为A的标准型，其左上角有一个r阶单位子块，其余元素全部为0,I与B1相乘的结果是取矩阵B1的前r行，其余行全部为零，因而根据命题4有:

R(IB1)≤R(B1)=R(B) .

从而R(AB) ≤R(B).

同样R(AB) ≤R(A).

而这类命题用第二定义来证明却是十分困难.

[1] 王萼芳,石生明.高等代数[M].3版.北京:人民教育出版社，2003:117-136.

[2] 邱森.高等代数[M].武汉:武汉大学出版社，2008:77-105.

[3] 刘丁酉.矩阵分析[M].武汉:武汉测绘科技大学出版社，1998:21-28.

[4] Jim Hefferon. Linear Algebra [M].USA: CreateSpace. 2008: 124-205.

[5] 同济大学数学教研室.线性代数[M].北京:人民教育出版社，1982:46-75.

[6] 薛有才,罗敏霞.线性代数(理工类) [M].北京:机械工业出版社，2010:50-71.

[7] 吴赣昌.线性代数(经管类)[M].北京:中国人民大学出版社，2007:72-75.

[8] 高克权.线性代数(高职高专规划教材) [M].北京:北京师范大学出版社，2009:26-45.

[9] 同济大学应用数学系.线性代数[M].4版.北京:高等教育出版社，2003:57-71.

[10] 齐民友,蔡德祺,刘丁酉.线性代数[M].武汉:武汉大学出版社,2003:72-81.

[11] 魏献祝.高等代数[M].上海:华东师范大学出版社,1997:82-89.