外部环境干扰下的非线性渔业资源种群动力模型及分析

顾恩国，范致鉴，梁 艳，廖容云

(中南民族大学 数学与统计学学院，武汉 430074)

随着全球人口数量的增加，渔业资源消耗也越来越多，近年来，渔业资源的可持续发展问题随着人口的增长和社会经济的快速发展日益突出，渔业资源的过度捕捞已经影响了资源种群的可再生能力和可持续利用[1].而渔场资源区域种群的可再生性开发利用使得生态经济模型逐渐受到学者们的关注，尤其是一些海洋渔业资源种群数量的锐减，也渐渐为人们所关注.这不仅关乎着生物圈食物链的完整性，而且也对人类与自然之间的和谐相处有极大的影响.

从人类需求的角度来看，在渔业资源的开发与管理中，捕食者-食饵系统模型在生物数量关系上起着根本的作用，许多学者[2，3]研究了连续的捕食者-食饵动力系统模型，获得了复杂的动力学行为，比如平衡点的稳定性、Bogdanov-Takens分叉、Hopf分叉、有限环等.也有学者[4，5]结合商业化行为添加捕捞力度对其改进，更有学者[6]考虑近年来的环境污染造成的有害物对鱼类种群的影响对模型进行修正.本文在借鉴前人研究的基础上，首先运用Euler方法对捕食者-食饵模型离散化，离散模型能很好地描述种群代与代之间不发生交叉影响的情况，在该模型中，捕食者种群的鱼直接或间接受到来自外部环境的干扰.通过对该离散数学模型的分析，我们丰富和发展了非线性动力学的正不动点、吸引域、吸引域边界结构等相关理论;反过来，这些理论能扩展模型的应用，对渔业资源种群数量的长期性、时效性演化做出合理的预测或预警，从而为渔业资源管理者提供有力的依据支持.

1 模型的建立

在海洋渔业资源中，种群的演化可以用捕食者与食饵(Lotka-Volterra prey-predator)相互作用的连续动力系统：

(1)

来描述，这里x=x(t)表示在t时刻的食饵种群的数量密度;y=y(t)表示在t时刻的捕食者种群的数量密度;r1是食饵种群的最大增长率;r2是在缺少食饵时捕食者的相关死亡率;k是指渔业资源区域食饵种群数量的环境承载能力.

假若渔业资源种群数量的代与代之间不发生交叉重叠，一些学者[7，8]主张用差分方程表示的离散模型要比连续模型更适合一些.应用欧拉(Euler)方法对模型(1)进行离散化，得到差分系统：

(2)

并注意到有学者[9]对一维的Logistic S型增长模型作改进时考虑了外部环境因素的扰动，受此启发对模型(2)考虑添加一外部环境下对捕食者种群的扰动项E来构建一个有关渔业资源两种群数量演化的离散非线性动力模型:

(3)

这里的扰动项E，E>0时认为是外来捕食种群从外部区域的迁入，或者是人类对捕食者种群数量的补充;E<0看作是商业活动下对捕食者种群数量的适时捕捞.

2 正平衡点的存在性和局部稳定性及局部分叉

将(3)式写成映射动力系统的形式：

(4)

求系统(4)的不动点，基于模型本身的意义，不动点应为正值，系统(4)的不动点满足x′=x,y′=y,即系统(4)的均衡点应满足下面的非线性方程组的解:

(5)

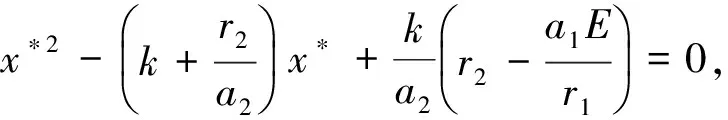
而系统(4)在平衡点的稳定性主要取决于其Jacobian矩阵的特征值，该矩阵在平衡点有如下形式:

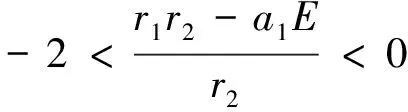
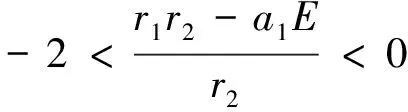
(2)关于正平衡点P2(x*,y*)，我们有：

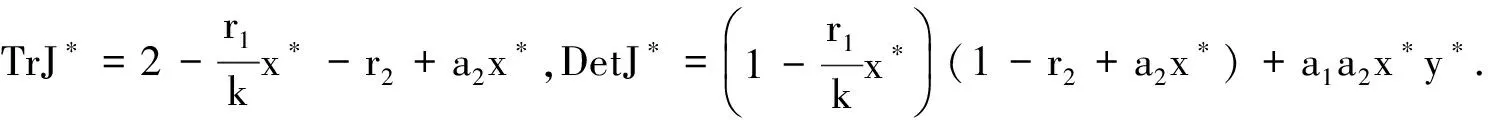
则有P(λ)=λ2-TrJ*λ+DetJ*=0.关于系统(4)在正平衡点P2(x*,y*)的稳定性，我们有下面的定理2.

定理2 (i)当在正平衡点P2处满足Jury条件[10]:

P(1)=1-TrJ*+DetJ*>0,P(-1)=1+TrJ*+DetJ*>0,1-DetJ*>0 时，系统(4)在正平衡点P2(x*,y*)处渐近稳定;

(ii)P(1)=1-TrJ*+DetJ*=0时，系统(4)在正平衡点P2(x*,y*)处将产生fold分叉;

(iii)P(-1)=1+TrJ*+DetJ*=0时系统(4)在正平衡点P2(x*,y*)处将产生flip分叉;

(iv)DetJ*=1时系统(4)在正平衡点P2(x*,y*)处将产生Neimark分叉.

(i)中的3个条件决定着复平面上是否有特征值能逃离单位圆，如果满足P(1)<0,则有一特征值大于1;如果P(-1)<0,则有一特征值小于-1;如果1-DetJ*<0,则有一对在单位圆外部的复特征值.

由于正平衡点的复杂性，在系统中k,r1,r2,a1,a2,E之间又是相互独立的参数，我们通过数值方法确定正平衡点的稳定性，当这些参数分别取k=5,r1=3.96,r2=0.6,a1=0.6,a2=0.3,E=0.18时，有P(1)≈1.4500>0,P(-1)≈2.4243>0,1-DetJ*≈0.0629>0.此时仅有一正平衡点P2(1.8554,4.1508)是稳定的.

为了能很好地研究系统(4)的吸引子结构随参数的变化关系，我们先画出一个关于参数k,E的二维分叉图.取初始值x0=2,y0=3并令r1=3.96,r2=0.6,a1=0.6,a2=0.3.通过像素扫描，我们得到k∈[2.6284,5.7282] 和E∈[-0.8333,1.1003]的二维分叉图(如图1)，能清楚地看到A区域表示系统稳定到正平衡点P2(x*,y*);B区域表示系统稳定到二周期点;如果参数值在C区域取值，系统稳定到周期大于10的吸引子，这种情形下就认为系统稳定到准周期或者是一个混沌吸引子;当参数k,E的值位于D区域时，我们就认为系统(4)是发散的或者是不稳定的.

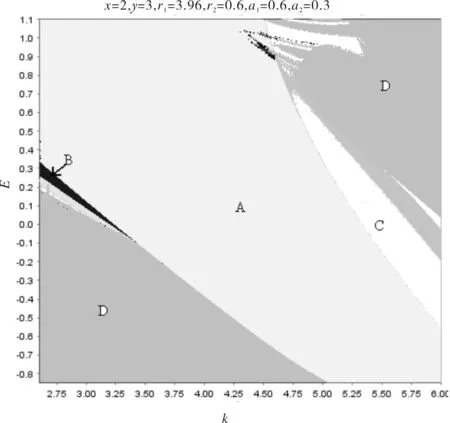
图1 系统(4)关于参数k∈[2.6284,5.7282] 和E∈[-0.8333,1.1003]的二维分叉图

然后通过图2对这个非线性动力系统做进一步分析，初始渔业资源数量取x0=2,y0=3.图2(a)为系统参数取r1=3.96,r2=0.6,a1=0.6,a2=0.3,E=0.18时关于参数k∈[2.6284,5.7282] 的一维分叉图，从图2(a)能清楚地看到包含周期合并、许多周期窗口、明显的倍周期分叉以及Neimark分叉.当r1=3.96,r2=0.6,a1=0.6,a2=0.3,E=0.18在满足k∈[2.8879,5.1480]时系统(4)在正平衡点P2(x*,y*)处将是渐近稳定的；参数在kkc4≈5.7009时，系统(4)稳定到周期大于10的混沌吸引子或者是准周期，使得渔业资源最后达到混沌状态，即资源在一定范围内出现周期波动.同样图2(b)中若取定k=5,r1=3.96,r2=0.6,a1=0.6,a2=0.3，获得一个关于E∈[-0.8333,1.1003]的分叉图，能够观察到在E∈[-0.8333,0.3378]时系统(4)在正平衡点P2(x*,y*)处渐近稳定，表明渔业资源稳定在一个正值(正平衡点)，并且它随着E的增加而减小；当E越过Ec1≈0.3379时，正平衡点P2(x*,y*)失去稳定产生Neimark分叉；当E越过Ec2≈0.5458时，系统(4)的不变闭曲线破裂产生五周期点；然而在区间E∈[0.5976,0.9610]内，出现了吸引子发散到无穷的奇怪现象，意味着渔业资源种群演化为爆炸危机，出现种群灭绝；而在E∈[0.9611,1.1003]时，又出现新的不变闭曲线，随着E的继续增加，不变闭曲线破裂使得系统(4)稳定到新的周期点或者演化为混沌吸引子.

图2 系统(4)关于承载能力k和扰动项E的一维分叉图

3 正平衡态的全局分析

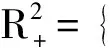
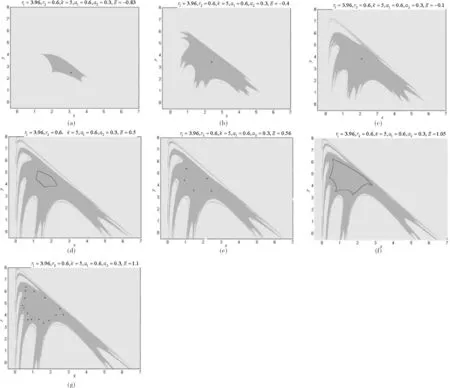
图3 系统(4)关于参数k=5,r1=3.96,r2=0.6,a1=0.6,a2=0.3随着E变化时的可行域和最终分叉

4 结语

本文构建了一离散的渔业资源两种群数量在外部环境干扰下的非线性渔业资源种群模型，并对模型进行了分析，得到正平衡点存在性和稳定性的条件范围，以及用数值模拟出可行吸引域、吸引子的变化，进而分析了渔业资源的捕食者种群数量在扰动项E干扰下资源枯竭的参数变化范围，也表明人类对渔业资源的过度干扰会使得资源更加容易枯竭，这对于资源管理决策者有效监控海洋渔业资源区域种群数量的稳定性和可持续利用有一定的参考意义.

[1] Garcia,Grainger J R.Gloom and doom? The future of marine capture fisheries[J].Philosophical Tanscations of the Royal Society ,2005,B360:21-24.

[2] Kar T K,Pahari U K.Modeling and analysis of a prey-predator system with stage-structure and harvesting[J].Nonlinear Anal RWA,2007,8(2): 601-609.

[3] Xiao D M,Li W X,Han M A.Dynamics in ratio-dependent predator-prey model with predator harvesting[J].Math Anal Appl,2006,324(1):14-29.

[4] Kumar S,Srivastava S K,Chingakham P.Hopf bifurcation and stability analysis in a harvested one-predator-two-prey model[J].Appl Math Comput,2002,129(1): 107-118.

[5] Kar T K,Matsuda H.Global dynamics and controllability of a harvested prey-predator system with Holling type III functional response[J].Nonlinear Analysis HS,2007,1(1): 59-67.

[6] Gakkhar S,Singh B.The dynamics of a food web consisting of two preys and a harvesting predator[J].Chaos Solitions and Fractal ,2007,34(4): 1346-1356.

[7] Murry J D.Mathematical biology[M].New York:Springer-Verlag,1989.

[8] Freedman H I.Deterministic mathematical models in population ecology[M].New York:Marcel Dekker,1980.

[9] Gu Enguo.The feasible domains and their bifurcations in an extended Logistic model with an external interference[J].Int J of Bifurcation and Chaos,2007,17(3):877-889.

[10] Gu Enguo.Global analysis of an ecological populational model with an external interference[J].Chaos solitions and Fractal ,2007,32 : 224-233.

[11] Gu Enguo,Rung J.On some global bifurcations of domains of feasible trajections:analysis of recurrence equations[J].Int J of Bifurcation and Chaos,2005,14(5): 1625-1639.

[12] Gu Enguo.Global bifurcations of domains of feasible trajectories:analysis of a predator-prey model[J].Int J of Bifurcation and Chaos,2006,16(8): 2601-2613.