一种多项指标全提升的多目标优化演化算法

宋中山，陈建国，郑波尽

(中南民族大学 计算机科学学院，武汉 430074)

演化算法是建立在自然选择和遗传变异理论之上的一种随机搜索技术[1].虽然用演化算法来解决最优化问题有较长的历史，但是多目标优化演化算法(MOEAs)的历史并不是很长，近年来，关于MOEAs的研究正在不断地升温.

目前，在MOEAs的研究中，基于Pareto和精英策略的演化算法占据了主流位置，其基本模式为：个体生成器策略+文档策略.在个体生成器策略中本文采用粒子群优化算法(PSO)，PSO没有使用遗传算法中的交叉及变异操作，而是粒子根据自己和同伴的历史行为来动态的调整自己的搜索位置.具有简单，容易实现；需要调整的参数少；收敛快速等优点.但是其收敛速度快，又容易出现早熟现象.在文档策略中本文采用快速文档处理算法----几何Pareto选择算法(GPS)[2]，大部分的文档算法都存在Pareto前沿点个数和算法时间复杂度之间的冲突问题，这样很难在有限时间内取得足够多的近似Pareto前沿点，而采用GPS的MOEAs具有以下优点：能以概率1收敛到射线Pareto前沿[3]；前沿点分布均匀；前沿点个数足够；时间复杂度仅为O(M)(M为目标数).鉴于以上两个算法的优越性，本文将PSO和GPS相结合来解决多目标优化问题，并且将针对多目标优化问题中的难点对PSO进行改进.

1 演化算法的特点

1.1 粒子群优化算法

PSO是一种基于群智能的演化计算技术，该算法于1995年由Eberhart博士和kennedy博士提出[4].

算法的基本思想：初始化一群随机解作为随机粒子，然后通过迭代找到最优解.在每一次迭代中，粒子通过跟踪两个“极值”来更新自己，第一个是粒子本身所找到的最优解，称为个体极值pBest，另一个极值是整个种群目前找到的最优解，称为全局极值gBest.

PSO每次迭代过程中只根据gBest和pBest来生成新的粒子，这是一个单向流动的过程，即整个的搜索更新过程是跟随当前最优解的过程，而遗传算法是通过染色体互相共享信息，使整个种群均匀地向最优区域移动.

1.2 几何Pareto选择算法

GPS算法是一种基于采样模式的文档算法[5].用文档来保存最优解，即获得了Pareto前沿点的采样，GPS算法是目前最先进的保存最优解的算法.

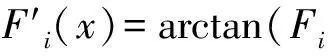
在GPS算法中，对于M维目标问题算法的总体时间复杂度为O(GMN)+O(MA2)，对于很多的MOEAs算法的时间复杂度，Jensen在文献[6]中都进行了讨论，对于NSGA2算法改进后的时间复杂度为O(GNlogM-1N)，SPEA2在处理二目标问题时为O((N+A)3/2log(N+A))，所以采用GPS的MOEAs具有较高的速度.在空间复杂度上，GPS算法的空间复杂度为O(NM-1)，在二维目标问题时并不比SPEA2和NSGA2等算法高.

2 多目标优化PSGPS算法

2.1 算法的基本思想

1)对于M维目标问题，将整个种群划分为M+1个子种群，前M个子种群中，每个子种群处理一个目标，而第M+1个用于获取折中解.

2)每个子种群的粒子采用PSO及一定概率的变异和杂交来生成新的粒子.

3)采用GPS来保存目前最优粒子.

4)通过迭代2)、3)来获得最终的近似Pareto前沿.

2.2 算法的难点及其解决方法

在本文中使用3种策略分别处理MOEAs中的极限点的获取、折中点的获取和文档算法.

1)极限点获取.所谓极限点，就是在某一个目标值上为最优，且该极限点为真实Pareto前沿上的点.极限点的获取对MOEAs非常重要，在于这些极限点刻画了真实Pareto前沿的边界，而且其周围的点常常也是真实Pareto前沿上的折中点.为了解决极限点的问题，本文在PSO算法中加入变异操作，确保从理论上PSO算法能够找到极限点.

2)折中点的获取.当PSO算法寻找极限点的时候，由于演化算法在局部最优点或者全局最优点附近常常会有重复的搜索，而这些点，很可能就是折中点，因此，算法不需要特意去寻找极限点附近的折中点.该假设成立的前提是：PSO所优化的各个目标比较复杂.当比较简单的时候，PSO可能直接就找到最优点，而不会在最优点附近做密集搜索.在PSO中，加入变异算子，也可以达到在目标值简单的情形下，获得较多折中解的目的.此外，为了获得更好的折中解，算法中加入一个跨子种群的仿射杂交算子.这一算子由于在各个极限点之间进行仿射杂交，因此，多数情况下，都能得到极限点中间的点，即折中解.在算法中，PSO除搜索M个目标外，还需要搜索一个折中的目标以发现更好的折中解.

3)文档算法.以上2个问题都属于搜索问题.文档算法则属于解的保存问题.本文使用GPS算法进行处理.

2.3 算法中各算子的介绍

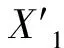
(1)

2) 变异算子.使用Delta变异算子，假设父体为X1=(x11,x12…,x1n)，随机选择一个基因x1j，β为一个小常数，令：

(2)

种群的划分策略.本算法中将种群划分为M+1个子种群，M为目标函数的个数.每个目标函数优化1个子种群，自定义第M+1个目标优化函数，用其来优化所有目标的平均值，并将这个函数取名为折中函数.用公式(3)表示：

Gi(x)=Fi(x),
Gi+1(x)=(F1(x)+F2(x)+…+Fi(x))/M.

(3)

better()函数用来比较2个个体的优劣.在优化最小化问题时，同一个种群中的个体在同一个目标函数下，如果新个体比旧个体在的函数值小，则返回true；如果函数值相同则使用比较两个点的占优关系以防止取得错误的极限点；如果优化目标为第M+1个目标，则根据折中函数进行比较，如果新个体的折中函数值小于旧个体的折中函数值，则返回true.

2.4 算法的总体流程

算法的总体流程如下.

算法PSGPS

初始化种群和文档

While (! Terminate ())

For i=1 to PopSize

采用PSO生成策略生成新的个体tmp

试着采用GPS算法将个体tmp加入到文档中

If Better (tmp,Indiv[i])then Indiv[i]:=tmp

else以概率为0.5的变异操作生成新的个体tmp2

试着采用GPS算法将个体tmp加入到文档中

If Better (tmp2,Indiv[i])then Indiv[i]:=tmp2

else 通过子种群的杂交操作生成新个体tmp3

试着采用GPS算法将个体tmp3加入到文档中

If Better(tmp3,Indiv[i])then Indiv[i]:=tmp3

End for

End While

消除文档中被占优的解

输出文档中的非占优解

3 实验及结果分析

为了验证算法的性能，我们选取了ZDT1、ZDT6、SPH2、KURS(KUR有2个函数，这里选择的是其中较难的，为与另一个区分，在本文中改写为KURS)、QV这些测试函数，并将实验数据跟SPEA2、NSGA2、PESA所得的数据进行比较，这些对比的数据可以从Zitzler的网址上下载到.

为了比较算法的优越性，我们引入2个指标S和D来度量超体积的多样性和近似度.超体积即解构成的空间，它是融合了算法解收敛性、均匀性、和解的个数的度量尺度，显然，占优的超体积越大，则算法的性能越好.S为超体积的大小，D用来度量超体积的差异.假设要度量算法A和B，S(A)为算法A所得到的解的超体积，D(A+B)为A算法所得解的超体积占优B算法所得解的超体积的大小，则D(A+B)=S(A+B)-S(B)，如果要比较D(A+B)和D(B+A)的质量则还需要定义一个指标Q，Q用来度量算法A，B所得解之间的占优比率，Q(A)表示A算法得到的解在A,B两个算法共同最优解中的占优比率.

(4)

(5)

下面列出对于各问题PSGPS算法一次运行及对比算法30次运行的结果.

问题1：QV(维数为100)，比较结果如图1所示.

图1 QV的比较图

问题2：ZDT1，比较结果如图2所示.

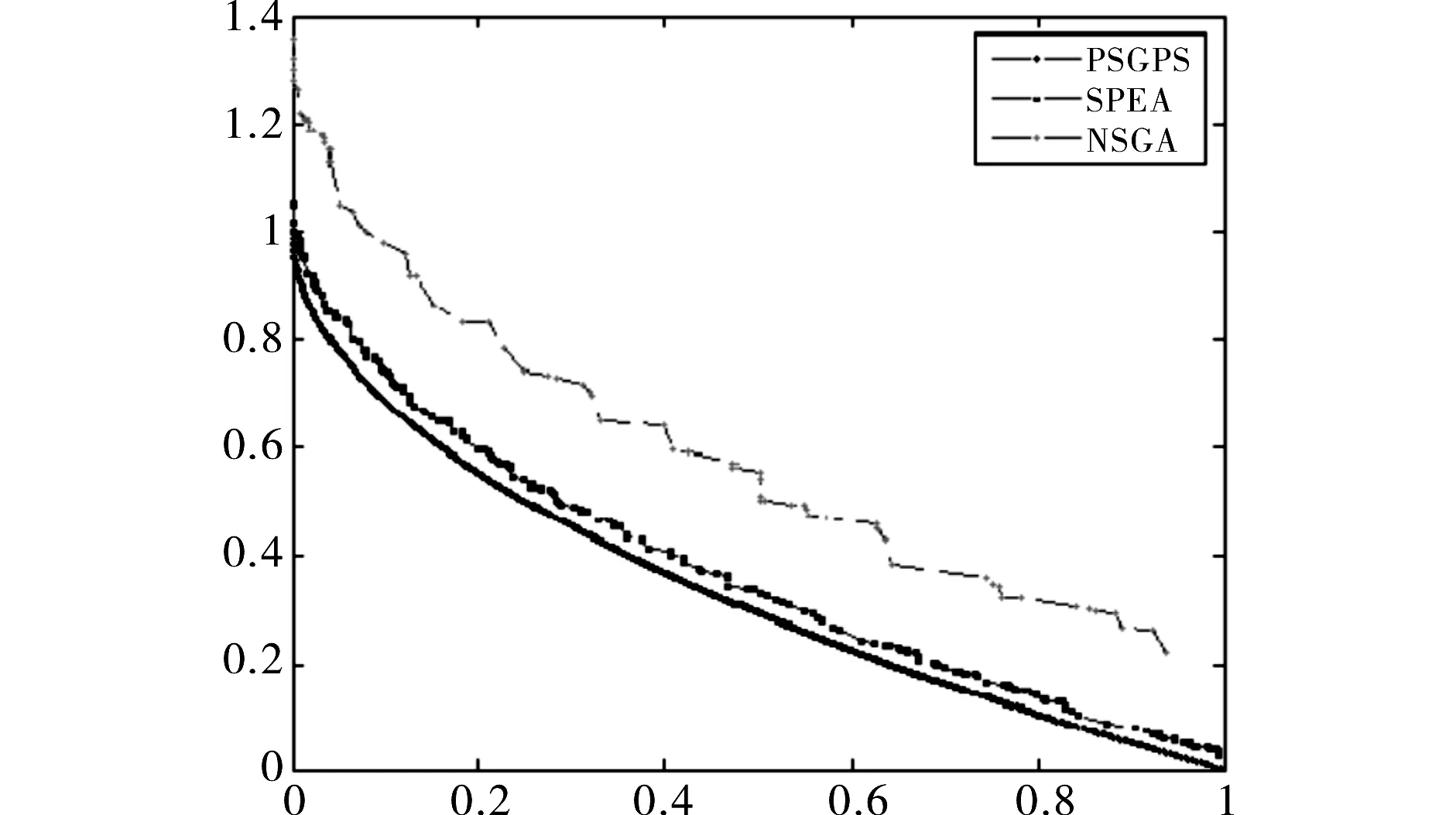
图2 ZDT1的比较图

问题3：ZDT6，比较结果如图3所示.

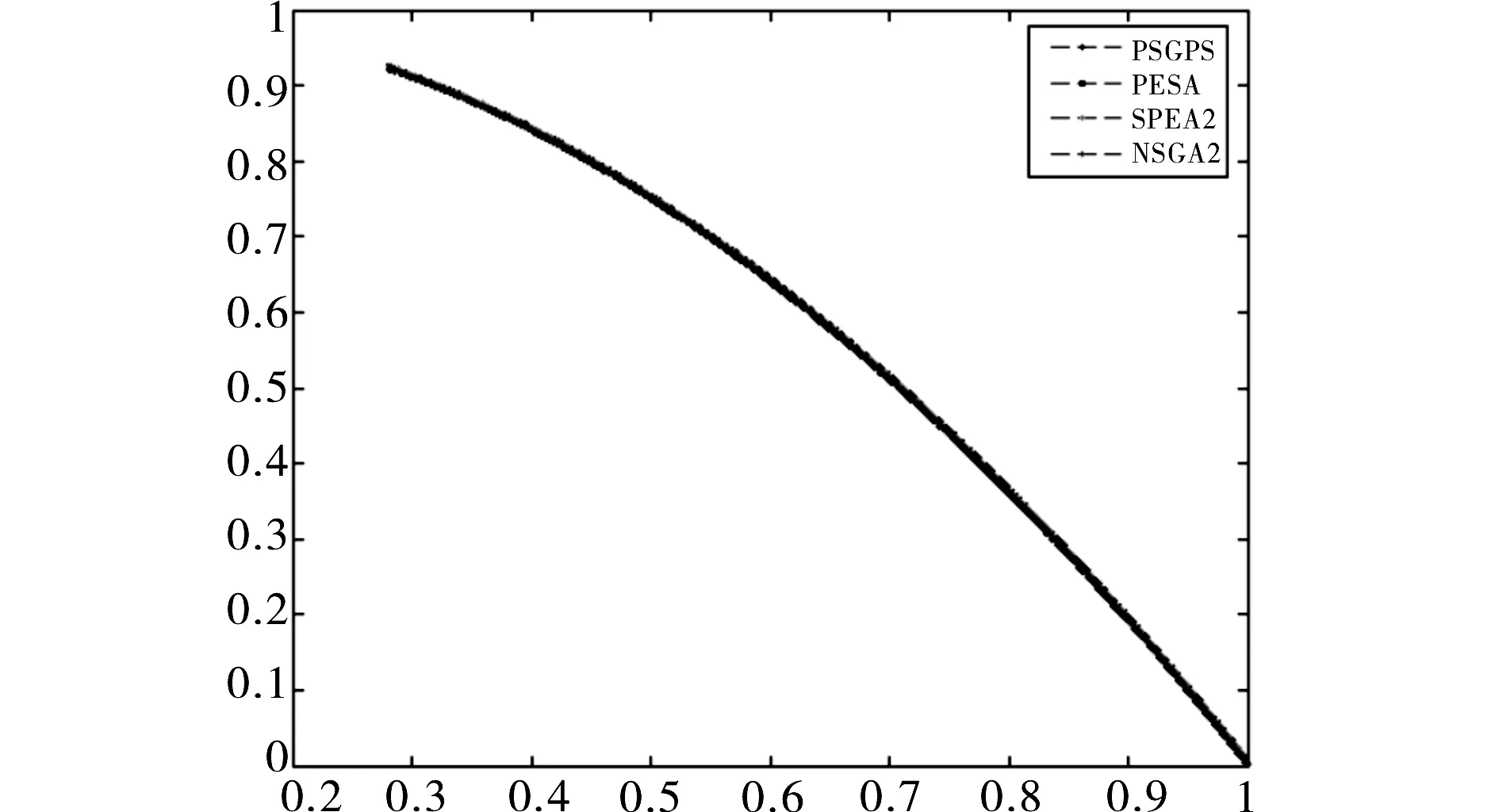
图3 ZDT6的比较图

问题4：SPH2 (维数为100)，比较结果如图4所示.

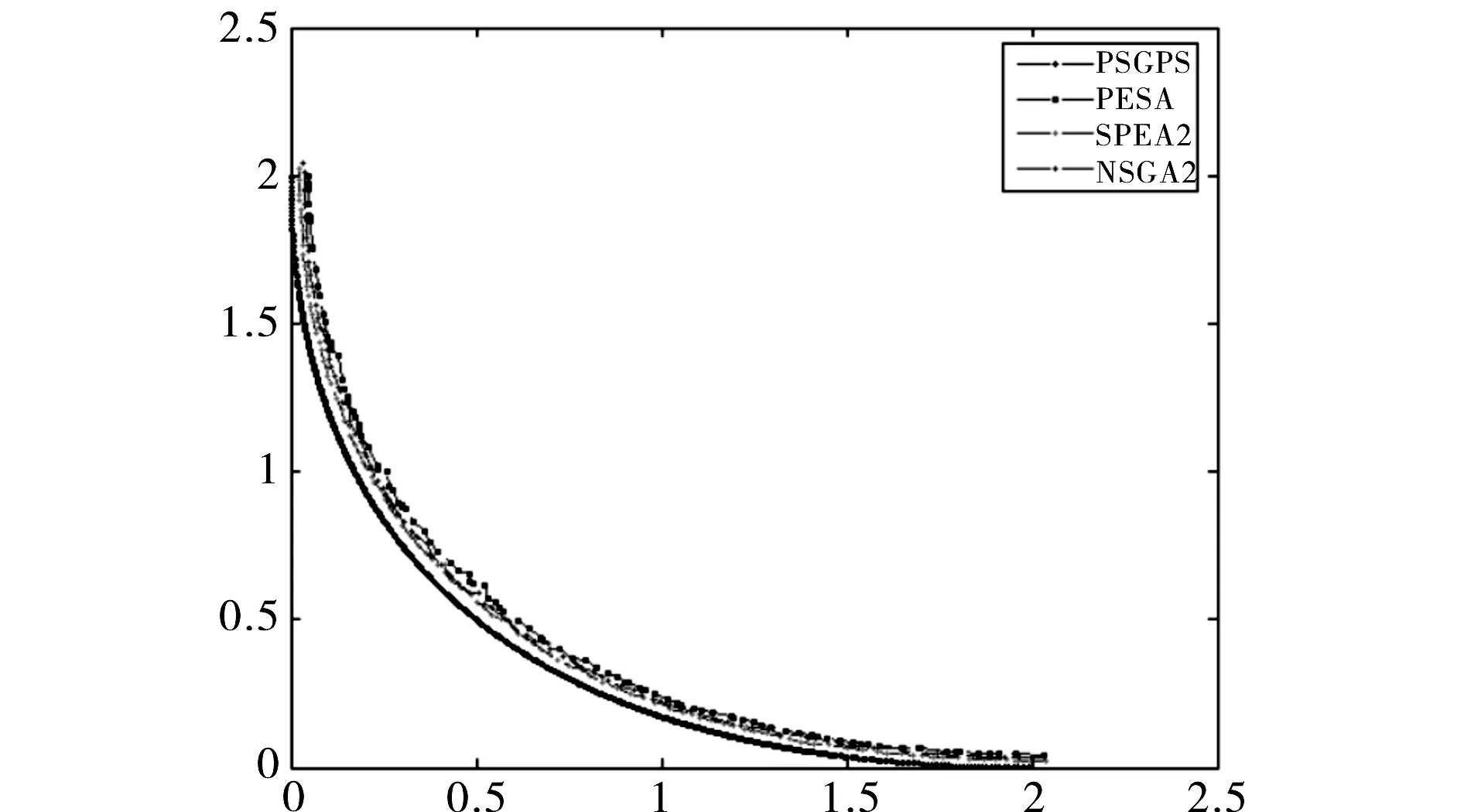
图4 SPH2的比较图

问题5：KURS，比较结果如图5所示.

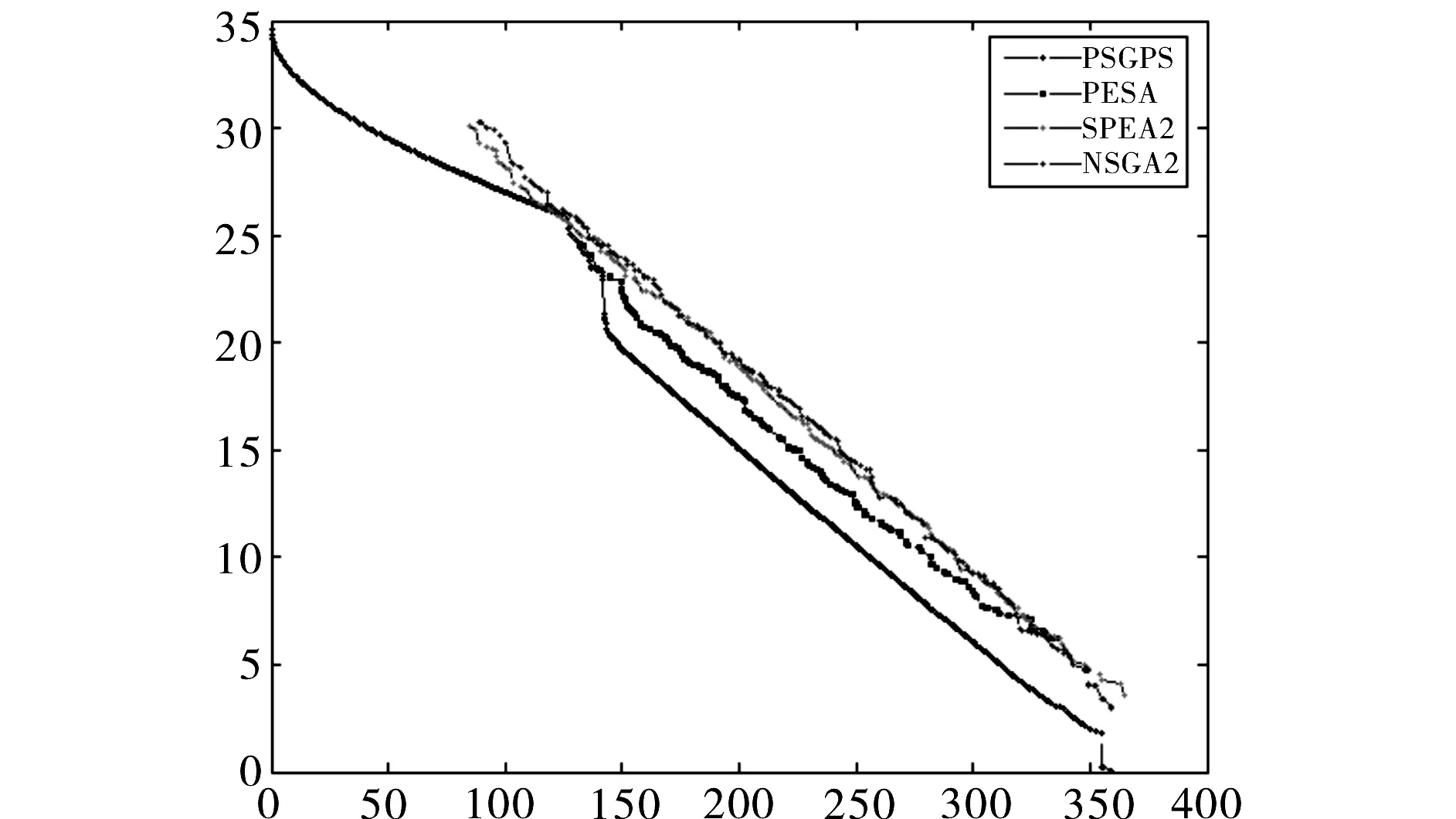
图5 KURS的比较图

从以上各个问题的对比图形可以看出本文算法所得的解非常好.经过统计分析可知，该算法在求解ZDT1、SPH2问题时所得到的解完全占优于其它对比算法的解，即占优比为100%，只在求解KURS、QV和ZDT6问题时不能完全占优.以下将这3个不能够完全占优的问题的各个指标列举出来，分别为表1，表2，表3.P、C分别表示PSGPS算法和对比算法，其中S(P)、S(C)分别表示本算和对比算法的S指标，D(PC)、D(CP)分别表示D(P+C)和D(C+P).

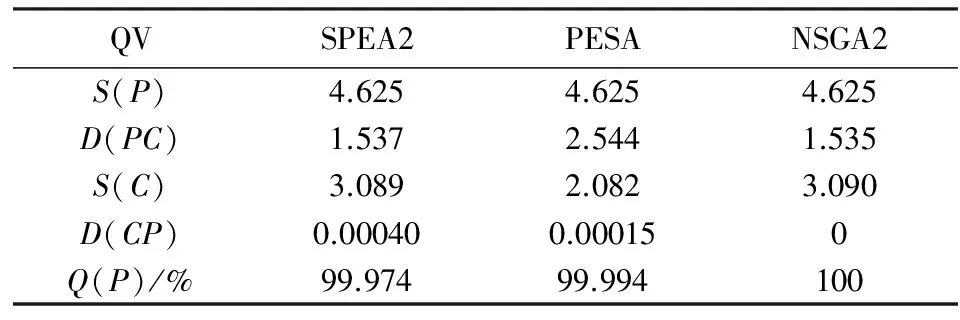
表1 QV问题的各个对比结果

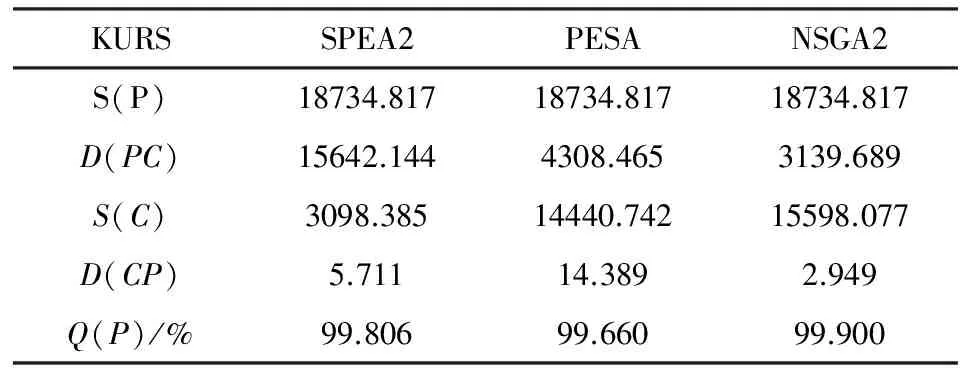
表2 KURS问题的各个对比结果

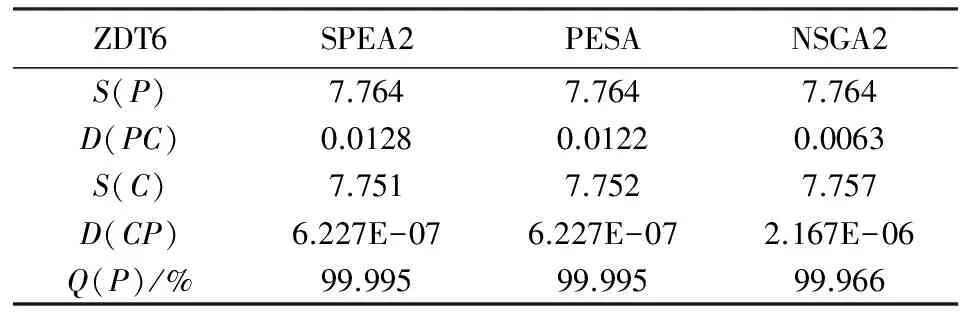
表3 ZDT6问题的各个对比结果

经计算，上述3个问题的占优比(Q测度值)都高于99%.这证明了该算法在结果的近似程度上远优于对比算法.

由于本文算法中的生成策略将种群分为M+1个子种群，自定义了1个目标函数，即折中函数.在二目标下，对于KURS这类简单问题，算法收敛速度过快，粒子很快可以收敛到两个函数极值点和折中函数的极值点.虽说种群更新中引入了一定概率的杂交和变异，仍可能出现两个邻近目标之间的区域不能够充分收敛到Pareto前沿的现象，如图5中横坐标为120～140的区域.经过分析，如果我们在原有的M个目标下引入更多的折中函数，上述现象就会得到解决.

该算法在速度方面也具有良好的性能，在Intel双核处理器主频1.86GHz的机器上以单线程运行，时间单位为ms.各个问题的运行时间如表4.

表4 各个问题的运行时间

4 结语

本文受PSO算法和GPS算法的启发，提出了一种高效的PSGPS算法.选取5个有代表性的多目标问题进行实验，结果表明：这个算法比当前的著名SPEA2，PESA，NSGA2等算法都要优越.在实验中，该算法的一次运行生成的解，无论是在数量上还是在均匀性上，都要比对比算法运行30次生成的解之和要好；在覆盖完整性上，其它算法在处理QV和KURS问题时都无法实现解的完全覆盖，而本算法做到了这一点；此外，本算法在时间复杂度上比其它算法要低.

算法在处理二目标时表现了良好的效果，在以后的工作中将希望实现三目标以上问题的解决；算法中采用的是数组存储精英解，但是当维数增加时，该算法需要更多的存储空间，如果采用其它的一些数据结构来存储精英解，有可能降低存储的空间；算法在处理QV、KURS和ZDT6问题时存在不能占优的解，如何采用更多的折中函数来使所得解能够完全占优，以上这些问题都有待进一步研究.

[1] Michalewicz.Genetic algorithm + Data structure =evolutionary programs [M].3rd rev and extended.Berlin: Springer-Verlag,1997:372-373.

[2] Zheng B.A highly efficient multi-objective optimization evolutionary algorithm [C]//ICNC.Proceedings-Third International Conference on Natural Computation.Jinan: ICNC,2007: 549-554.

[3] 周育人,闵华清.多目标演化算法的收敛性研究[J].计算机学报,2004,27(10): 1415-1421.

[4] Eberhart R ,Kennedy J.A new optimizer using particle swarm theory[C]//ISMMHS.Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Nagoya:ISMMHS,1995: 39-43.

[5] 郑波尽.演化优化方法研究[D].武汉:武汉大学，2006.

[6] Jensen M T.Reducing the run-time complexity of multi-objective EAs: the NSGA-II and other algorithms[J].Evolutionary Computation,2003,7(5): 503-515.