铣削加工薄壁工件的变形仿真

薛 飞

（上海电机学院 机械学院，上海 200245）

铣削加工薄壁工件的变形仿真

薛 飞

（上海电机学院 机械学院，上海 200245）

以平板薄壁工件为研究对象，在Matlab平台实现其铣削加工过程的变形仿真。根据瞬时刚性力学模型将轴向铣刀离散化处理，得到微元的切削力，进而求得整个铣刀切削力，建立了铣削加工过程铣削力模型。利用理论计算和有限元分析方法，推导了平板薄壁工件有限元模型的变形控制方程。模拟了铣削过程中瞬态铣削力和变形量的相互作用，预测了工件在铣削力作用下的变形情况。通过实例验证了该仿真方法的可行性与有效性。

铣削力；薄壁工件；变形仿真

薄壁结构件广泛应用于航空、能源、船舶等加工制造业，特别是追求高强度、轻质量的航空领域尤为突出。但薄壁类工件相对刚度较低，在铣削加工过程中易发生变形，切削力对加工精度的影响较为显著［1-3］。对于薄壁类工件，当工件材料确定后，主要从数控加工工艺角度对零件加工变形进行控制。若要有效控制加工变形，必须首先掌握加工变形的变化规律，即重视加工变形的预测分析研究［4］。目前，常用商业有限元软件进行变形分析，但由于铣削加工的断续性，以及工件进给的同时伴随着刀具旋转的特点，仿真技术还无法解决加工过程中刀具与工件之间的旋转接触问题。本文建立了加工过程中铣刀对工件铣削力的模型，将瞬态切削力作为载荷施加于铣削加工的薄壁工件模型上，通过薄壁工件有限元模型变形控制方程的仿真，实现工件的加工变形仿真。

1 铣削力模型

铣削过程建模研究一直是众多学者的研究热点［5-13］，其建模方法可归纳为经验法、分析法和力学法等几种。其中，应用最为广泛的为力学建模法。虽然力学法建立的切削力模型形式很多，但实质都是将切削力看成切削过程中的几何属性和物理属性的函数。

分析立铣刀的铣削力时，将铣刀沿轴线方向分割成具有一定高度的切削刃微元，从而使得切削齿线在每个切削刃微元上都是直线，如图1所示。

图1 立铣刀切削刃微元示意图Fig.1 Schematic of end milling tool cutting element

第ith个刀齿上高度为Δz的第jth个切削刃微元的加工力取决于这个切削刃微元的瞬态进给量fi、切削深度d和切削速度v，并以式（1）的非线性关系关联：

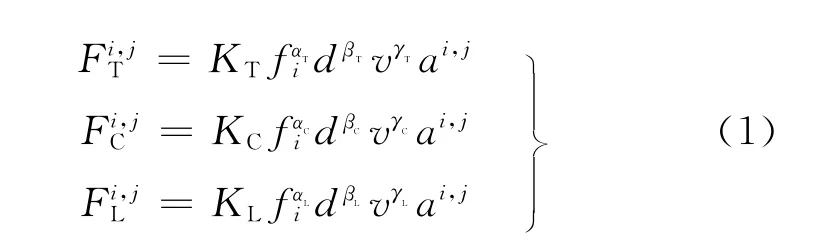
式中，Fi，jT为径向力；Fi，jC为切向力；Fi，jL为侧向力，它们都作用于ith刀槽的jth分层；fi为第ith刀槽的瞬态进给量；ai，j为第ith刀齿、第jth分区的切削面积；其余皆为切削力系数。

切削力的理论公式来源于刀具的径向、切向和侧向3个方向，刀具力的检测通过x，y，z方向得到。一般习惯于以工具的坐标x，y，z方向来表示切削力，故将切削力理论值变换到刀具坐标的x，y，z方向。

由于螺旋角的存在，导致切削刃上的点将比铣刀底刃端点滞后。第ith刀齿上第jth切削刃微元处的瞬时径向接触角可表示为

式中，θj0为第ith刀齿的第1分区角度；j为分区数量；Nf为齿数；β为刀具的螺旋角度；Δz为刀齿所在分区的切削深度；Rt为刀具半径。

每个刀齿每个分区上x，y，z方向的作用力通过对作用在相同刀齿分区的径向、切向和侧向力的坐标变换，由下式得：

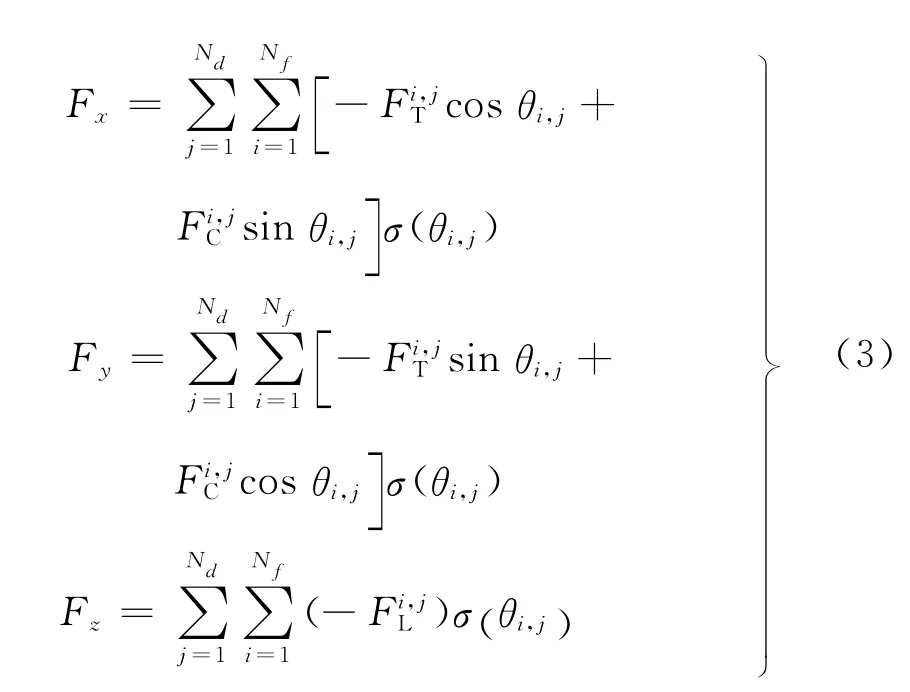
式中，Nd为分层数；σ（θi，j）为判断刀具是否和工件接触的函数，若接触为1，否则为0。

2 工件变形控制方程

本文选择平板结构的薄壁件作为铣削加工分析对象，可将其简化为悬臂梁［14-15］，薄壁平板的受力简化图和微元受力分析如图2所示。

图2 平板节点微元受力分析Fig.2 Force diagram of flat workpiece element node

图2中，x为平板的水平方向；y为平板的变形量；q为均布载荷；Fs为平板内力；M 为平板所受弯矩。各载荷随时间t变化，t和x方向位移2个变量函数根据动量守恒定律，对微元在自然坐标系上建立动力学方程：

式中，mL为单位质量。整理得

由弯矩平衡得

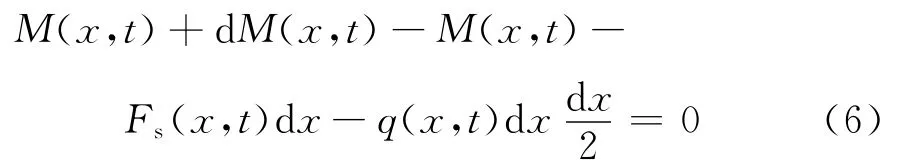
忽略式（6）最后1项高阶项，整理得

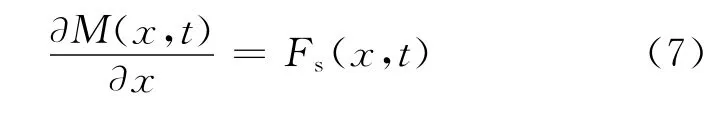
挠度与x点处的弯矩之间的关系式为

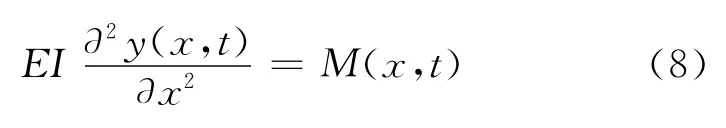
式中，E为弹性模量；I为惯量。假设平板各向同质，mL，E和I均不是关于x的函数，忽略x方向的重力作用。将式（7）和（8）代入式（5），得变形控制方程为

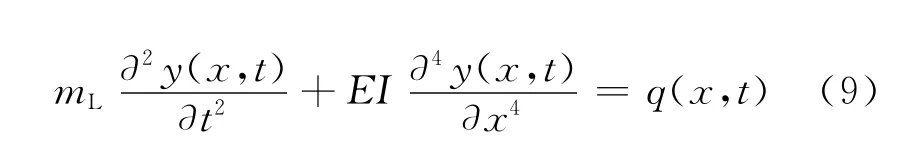
3 基于Matlab的变形预测

金属铣削加工是一个连续的过程，要实现加工过程的仿真需要将这一连续过程离散化，可在Matlab平台实现仿真，具体方法如下。

（1）计算刀齿的旋转角度。计算初始时刻的刀齿角度为

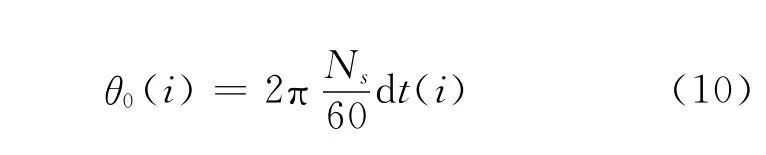
每一瞬时每个刀齿的角度为

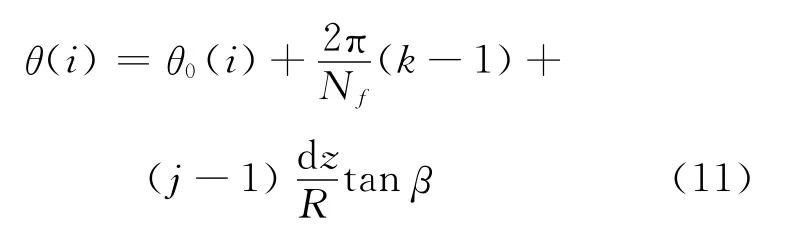
（2）判断刀齿处于有效切削范围。θen为铣刀齿切入角，θex为铣刀齿脱离工件时的切出角，切入角和切出角的大小由铣刀和工件的结构决定。用σ（θ（i））来判断刀齿是否处于切削范围，即

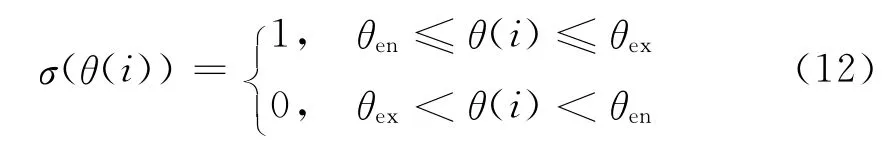
（3）切削载荷施加。在切削仿真过程中，需要建立刀具的切削点与工件有限元模型上的节点对应关系，然后把切削载荷按一定比例关系分配到对应的工件节点上。

式中，a1为切削载荷的作用点坐标值；Vr为进给量；L为平板长度；N为微元总数。

4 仿真实例

薄壁类零件是最容易变形的零件之一。本文以不锈钢工件材料的梁类薄壁零件为对象，结构尺寸为100mm×4mm×2mm。刀具半径为0.5mm，2齿，螺旋角为40°。切削参数中主轴转速为1 000r／min，切削深度为0.2mm，进给速度为100mm／min。工件的边界条件是在端部施加固支约束。工件铣削示意图如图3所示。

对工件施加100N的负载于70mm的位置，阶跃输入时域响应仿真结果如图4所示。工件经过几次振荡，其末端变形量在约80ms时稳定在0.036mm的位置。

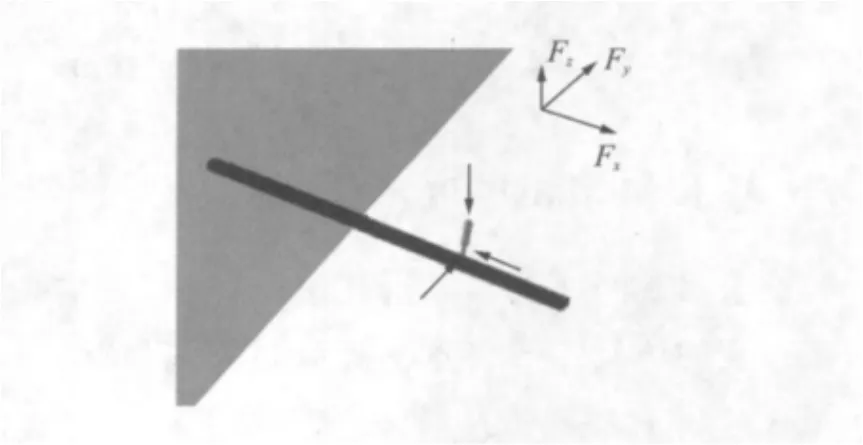
图3 薄壁工件铣削示意图Fig.3 Schematic of machining process for thin－wall workpiece

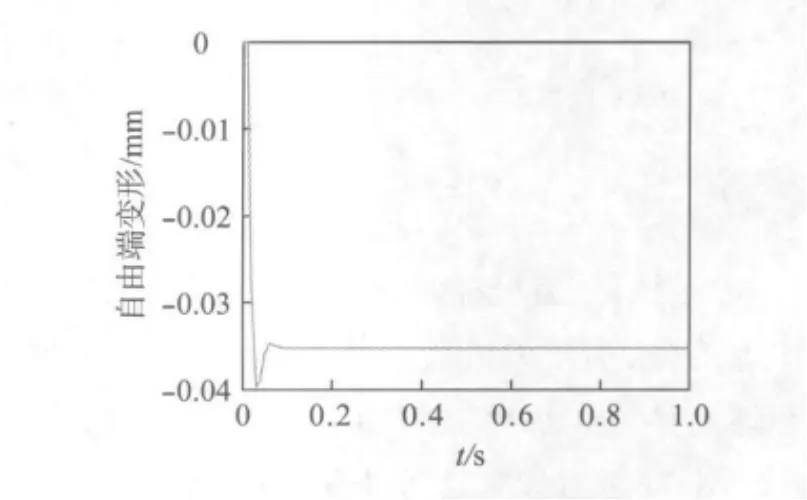
图4 工件阶跃输入时域响应仿真结果Fig.4 Step input response of workpiece

将铣削力系数、刀具参数等代入Matlab软件编制的仿真程序，得到铣削力仿真结果如图5所示。薄壁类工件铣削加工的弹性变形主要是由z方向铣削力Fz的变化引起的，故选取z方向的铣削力进行变形分析。

图5 铣削力仿真结果Fig.5 Simulation result of cutting force

当铣刀沿刀位轨迹以100mm／min的进给速度走刀5s时，薄壁工件在铣削力z方向的整体变形如图6（a）所示。薄壁工件末端端点的位移在铣削力Fz的作用下经过振荡达到平衡，变形量为9.2～6.1μm。由于薄壁工件自身的振荡频率低于铣削力的变化频率，故薄壁工件末端端点的变形振荡频率远低于铣削力的变化频率。离薄壁工件固定端长度x方向越远，薄壁工件的变形就越大。当铣刀以100mm／min的进给速度沿x轴的反方向铣削薄工件，走刀5s时，薄壁工件的变形如图6（b）所示。

图6 薄壁工件变形图Fig.6 Deformation of workpiece

两个工况比较可知，在铣削力的相关切削参数没有变化，Fz的大小方向也未改变时，末端端点位移随时间的变化趋势相同，不同的是变形振荡，负向进给时为6.7～4.3μm。当铣刀正向进给和反向进给铣削加工5s时，Fz的作用位置分别为78mm和61mm，杆件的变形量不同，符合一端固定悬臂梁的变形趋势。

5 结 语

薄壁工件的加工变形预测与精度保障是长期困扰我国制造业的技术难题。以瞬时刚性力学模型为基础，将轴向铣刀离散化处理，得到微元的切削力，进而求出整个铣刀切削力。通过建立铣削加工过程铣削力模型，为工件加工变形仿真提供计算基础。建立了薄壁工件的有限元模型，在Matlab平台上实现工件变形仿真。通过实例仿真分析证明，和商用有限元软件比较，应用该仿真方法有效提高了计算效率，为铣削加工工艺参数的进一步优化选择奠定了基础。同时，薄壁工件的振动变形不仅影响工件的加工精度、粗糙度，其与加工过程中的振动以及动态切削力密切相关，为仿真模型薄壁铣削加工领域的控制、颤振和粗糙度等方面的研究提供了理论基础。

［1］ 董耀跃，柯映林，杨慧香.薄壁板高速铣削加工过程中的让刀误差预测［J］.浙江大学学报：工学版，2006，40（4）：634－637，703.

［2］ 万 敏，张卫红.薄壁件周铣切削力建模与表面误差预测 方 法 研 究 ［J］.航 空 学 报，2005，26（5）：598－603.

［3］ Kim H S，Ehmann K F.A cutting force model for face milling operations［J］.International Journal of Machine Tools and Manufacture，1993，33（5）：651－673.

［4］ 陈秀生，张承瑞，刘日良，等.基于表面粗糙度预测的数控车削加工物理仿真模型的研究［J］.工具技术，2007，41（1）：36－39.

［5］ Landers R G，Ulsoy A G.Model－based machining force control［J］.Department of Mechanical Engineering and Applied Mechanics，2000，122（3）：521－528.

［6］ Kim S I，Landers R G，Ulsoy A G.Robust machining force control with process compensation［J］.Journal of Manufacturing Science and Engineering，2003，125（3）：423－431.

［7］ 李忠群，刘 强.圆角铣削颤振稳定域建模与仿真研究［J］.机械工程学报，2010，46（7）：181－186.

［8］ Budak E.Analytical models for high performance milling.Part II：Process dynamics and stability［J］.International Journal of Machine Tools and Manufacture，2006，46（12／13）：1489－1499.

［9］ Li Zhongqun，Liu Qiang.Solution and analysis of chatter stability for end milling in the time－domain［J］.Chinese Journal of Aeronautics，2008，21：169－178.

［10］ 王启东，刘战强，汤爱民，等.球头铣刀瞬态切削力数学模型建立与仿真［J］.农业机械学报，2011，42（8）：200－206.

［11］ Tsai C L，Liao Y S.Prediction of cutting forces in ball－end milling by means of geometric analysis［J］.Journal of Materials Processing Technology，2008，205（1／3）：24－33.

［12］ Kardes N，Altintas Y.Mechanics and dynamics of the circular milling process［J］.Journal of Manufacturing Science and Engineering，2007，129（1）：21－31.

［13］ 康永刚，王仲奇，吴建军，等.立铣切削力分类研究及精确铣削力模型的建立［J］.航空学报，2007，28（2）：481－489.

［14］ 李江涛，王纬波，吴有生.二端连续元件动力学特性的矩阵描述法［J］.振动与冲击，2010，29（9）：142－145.

［15］ Thomson W T.Theory of vibration with applications［M］.New Jersey：Prentice Hall，1988：213－232.

Deformation Simulation for Thin－Walled Workpiece of Milling Process

XUE Fei
（School of Mechanical，Shanghai Dianji University，Shanghai 200245，China）

To study deformation of thin－walled workpiece in milling processes，simulation of the milling process on the MATLAB platform is performed based on a study of thin－wall workpiece.According to the transient cutting force model，the end mill is sliced into disks with small element，the cutting force of each is analyzed and modeled.Consequently，the total cutting force is calculated.It is analyzed and modeled.Consequently，the total cutting force is calculated.Combining the analytical method and the finite element method，agoverning equation of deformation of the numerical model of thin－walled workpiece is derived.With the interaction between the transient cutting force and deformation during the milling process，prediction of the workpiece deformation with milling force is obtained.By analyzing the deformation simulation，feasibility and effectiveness of the proposed simulation approach is verified.

milling force；thin－walled workpiece；deformation simulation

TG 502.15

A

2095－0020（2011）06－0351－05

2011－10－19

上海市教育委员会重点学科建设项目资助（J51902）

薛 飞（1980－），女，副教授，博士，专业方向为机械工程，E－mail：xuef＠sdju.edu.cn