局部插值的H-Bézier曲线分段光顺拟合
张龙飞, 檀结庆
(合肥工业大学 数学学院,安徽 合肥 230009)
局部插值的H-Bézier曲线分段光顺拟合
张龙飞, 檀结庆
(合肥工业大学 数学学院,安徽 合肥 230009)
文章提出了一种基于局部插值的光顺拟合方法,通过对给定的离散数据点进行逐段拟合,可以完整地表现出已知数据点的分布情形;还给出一种改进的光顺准则,针对不同情况确定光顺约束方程之后,通过调整控制顶点及可能存在的曲线控制参数,使曲线的光顺能达到极小,从而得到较为理想的光顺拟合曲线。数值实例说明了该文算法的有效性。
H-Bézier曲线;分段拟合;光顺;能量法;曲率
在计算机辅助几何设计中,常会遇到给定数据点列,要求构造一条(张)部分通过此点列的曲线(面),使得曲线(面)能够较好地反应数据点列所表现的形状,有时候还要求构造光顺的曲线曲面来拟合给定点列,船舶业及航空工业中就经常使用光顺的曲线曲面来拟合给出的数据点,这涉及光顺和拟合的问题。工业设计中,判别曲线光顺与否的标准有很多种[1],较为常见的光顺方法是能量法。三次样条曲线的交互式光顺技术由文献[2-3]提出,并在此后得到了快速的发展,如节点删除插入法[2-4]、Kjellander算法及其改进算法[3-5]等。
近年光顺拟合的研究较多,如文献[6-8]。光顺准则一般采用改进后的光顺方法,比如既考虑到应变能又考虑到应力能等其他因素的光顺准则[6]。拟合时一般是在最小二乘法的基础上使用一条曲线去拟合,但仅用一条曲线拟合给定的数据点所得到的曲线并不能够很好地反映出数据点的整体情况,分段拟合可以更为准确地反映出数据点整体分布状况,局部插值可以在需要的地方增进对数据点的逼近程度,将分段拟合与光顺处理相结合在工程设计中有较大的用处。综上所述,分段光顺拟合有其研究的必要性。
本文提出了一种逐段光顺拟合的算法,给出了一种改进的光顺模型,其中考虑了光顺前后的控制顶点的偏差以及光顺后曲线与所给定的数据点的偏差,解决了光顺后曲线与原拟合曲线间偏离可能较大的问题,并在光顺拟合的同时实现段与段之间的光滑拼接。大家所熟知的H-Bézier曲线(面)不但保留了Bézier曲线(面)的优点,还可精确表示悬链线(面)、螺旋线(面)等工程中常见的曲线,虽然目前对于H-Bézier曲线的基本理论、分割拼接及形状分析都有学者做了研究[9-11],但关于 H-Bézier曲线(面)光顺的研究成果还比较少。鉴于低次曲线在工程实践中应用范围较广,本文使用三次H-Bézier曲线为例来验证算法的有效性。
1 三次H-Bézier曲线的定义
定义1 设hi∈R2(i=0,1,2,3)为控制顶点,α是大于零的任意实数,则曲线

2 改进的光顺准则
判别一条曲线光顺与否的标准有很多种[1],较为常见的方法是能量法,曲线光顺中的能量法一般是相对于曲线的应变能而言的。所谓应变能是指以应力和应变的形式贮存在物体中的势能,又称变形能,在用能量法光顺曲线p(t)时,人们通常建立的函数是对曲线按弧长取关于曲线曲率的积分,即应变能:
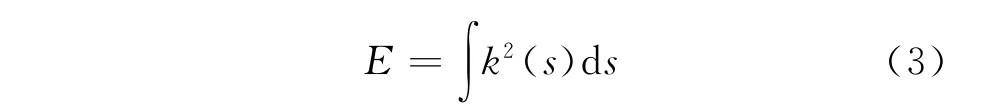
其中,k为曲率;s为弧长。
由于(3)式计算起来较为复杂,通常以其近似形式来逼近,即
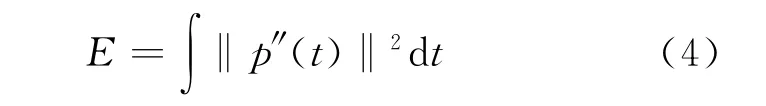
能量法与曲线的绝对曲率相关,能量趋小会使得曲线趋于直线化,但曲线整体的曲率变化却未必均匀。而剪力跃度的平方和与曲线曲率的变化相关,当剪力跃度的平方和较小时,曲线的曲率变化较为均匀。当知道n+1个点处的相对曲率以及它们之间的弦长时,可以得到剪力跃度的平方和[12-14]。令
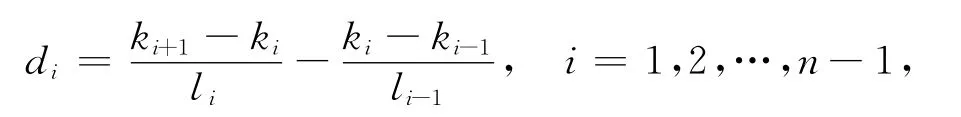
其中,ki为p(ti)点的曲率值;|di|为剪力跃度;li为p(ti-1)到p(ti)的弦长。
将剪力跃度的平方和整合进能量法,可以得到新的能量函数:
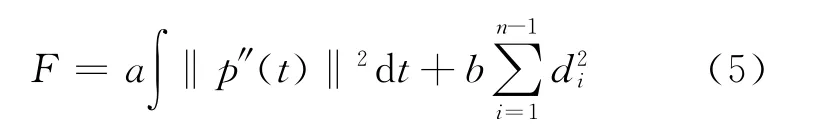
其中,a+b=1,a>0,b>0。在使用以上光顺准则对曲线光顺之后,原曲线与光顺后的曲线之间的偏差可能比较大。
本文针对以上问题将光顺前后的控制顶点的偏差以及光顺后曲线与所给定的数据点{Pi}ni=0的偏差考虑进来。因此,在给定偏差最大值ε1(控制点偏差)及ε2(数据点偏差)时,就应在
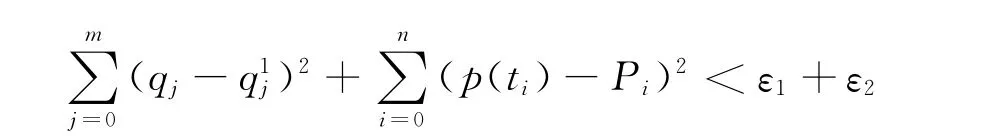
的条件下,使得能量函数F极小。其中,m为拟合出来的曲线次数;qj为原曲线的控制顶点;q1j为光顺后的控制点。由此得到改进后的光顺模型:
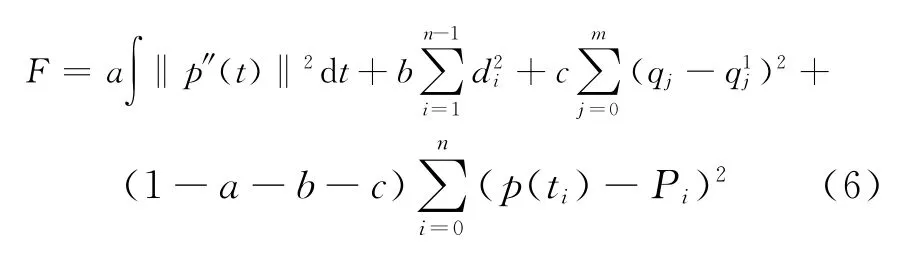
其中a,b,c∈[0,1],0≤a+b+c≤1。对于给定m次曲线c,记其控制顶点为q0,…,qm。
在实验过程中注意到这样一个问题,给定的采样数据点中,有一些数据点与可以精确逼近大部分数据点的最终拟合曲线之间的距离较大,若光顺时将所有数据点的作用看作同等,则光顺后得到的曲线与原拟合曲线间偏差会比较大,减小这类数据点的作用,可以得到与拟合曲线偏差不大且光顺效果较好的光顺曲线。
因此,在确定光顺函数时,应该考虑这一因素,使得拟合后距离拟合曲线较近的数据点起的作用大一些,距离拟合曲线较远的数据点所起的作用小一些。
实际操作时,可以给每一个数据点加上权系数{wi}ni=0。首先计算每一个采样数据点{Pi}ni=0与最终拟合曲线的距离,记为{edi}ni=0。对采样数据点按距离拟合曲线的远近排序,距离曲线最近的为首数据点,距离曲线最远的为末数据点,结果记为{P′i}ni=0,同时将数据点{Pi}ni=0与拟合曲线的距离按从大到小的顺序排序,所得结果记为{ed′i}ni=0。 由 此 得 到 排 序 后 的 每 一 个 数 据 点{P′i}ni=0的权系数{w′i}ni=0,即
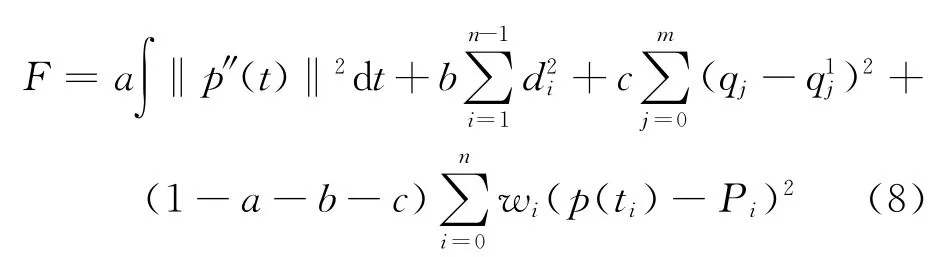
由此得到数据点Pi的权系数wi。将这一权函数加入到光顺函数中有:
令F→min,即可得到光顺后曲线c′的控制顶点q10,…,q1m,即
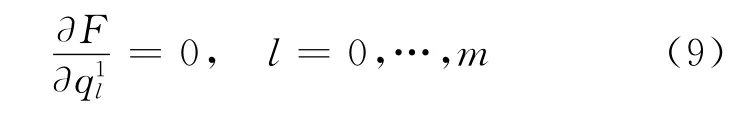
解方程组(9)可求得曲线光顺后的新控制顶点,从而得到光顺后的曲线。当需要光顺后的曲线仍通过首末端点时,有q0=q10,qm=q1m,(9)式转化为:
使用方程组(10)代换方程组(9)即可。
当需要光顺拼接时,则在(7)式的基础上加入拼接条件,以G1拼接为例,记前一段m次曲线为c1,其控制顶点为q1,0,…,q1,m,后一段n次曲线为c2,其控制顶点为q2,0,…,q2,n,记其在光顺后的控制顶点为q12,0,…,q12,n,为使c2在光顺后能与c1达到G1拼接,则应有:
将(11)式作为(9)式的约束条件,得到带有约束条件的光顺模型:
解这一含有约束条件的优化问题,可求得满足条件的解。
3 曲线拟合
本文在做曲线拟合的时候,采用最小二乘法来拟合给定的数据点列。设给定数据点列为拟合出来的曲线为p(t),其控制顶点为q0,…,qm。
局部插值的最小二乘拟合方法如下:
(1)对给定的数据点做累加弦长参数化:
其中,lj=|Pj-Pj-1|是Pj到Pj-1的弦长。
(2)设若希望拟合出来的曲线通过n+1个数据点中的N(N<m+1)个,记这N个点参数化后的点为tN,0,…,tN,N-1(将这 N 个点按顺序表示,仅为方便记)。将tN,0,…,tN,N-1代入p(t),则有p(tN,i)=0,i=0,…,N-1。以上N 个方程,共包含m+1个未知量,将q0,…,qN-1用余下的m+1-N个自由未知量表示出来。再求p(t)对这m+1-N个自由未知量的偏导并使偏导等于零,从而得如下方程组:
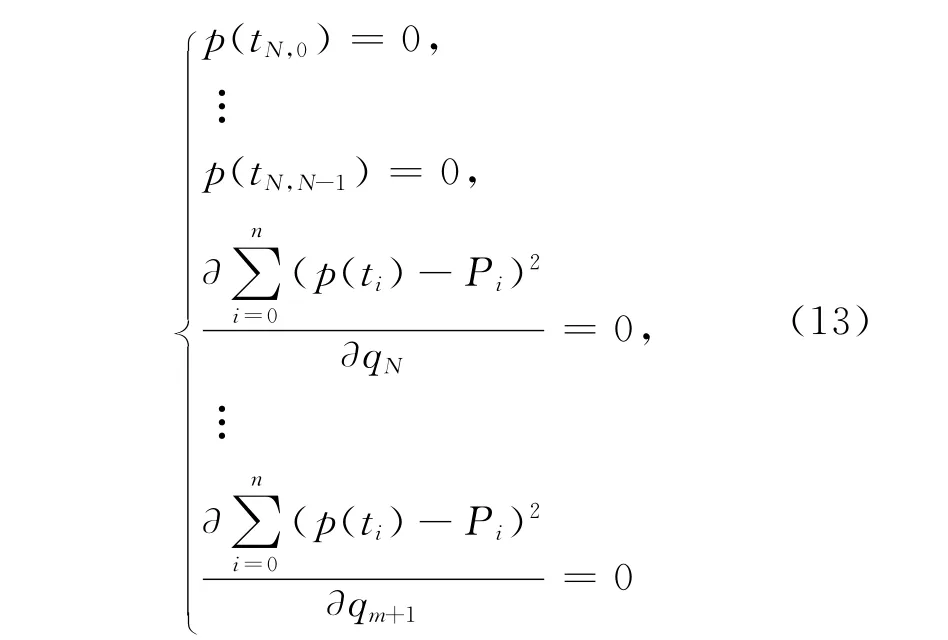
(3)解(13)式可得q0,…,qm,求出m 次拟合曲线。如果希望曲线通过首末数据点则有q0=P0,…,qm=Pn,代入(13)式可简化计算量。
4 分段光顺拟合算法
本文提出的局部插值分段光顺拟合算法,可以逐段拟合光顺,通过上一段的光顺对下一段的光顺做相应调整,使得前后段拟合曲线在连接点处能够达到G1连续。设拼接点的前一段曲线控制顶点为q0,q1,q2,…,qn,后一段曲线的控制顶点为v0,v1,v2,…,vn,qn=v0为拼接点。若要连接处达到G1连续,则需2段曲线的控制顶点满足如下关系:
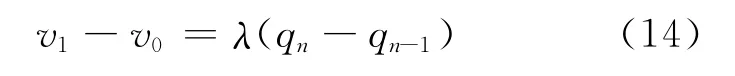
从而保持它们切向连续,可以允许它们模长不相等[14-15]。
如果需要曲线在拼接点处达到G2连续,就需要计算其二阶导数,在拼接点处的二阶导数满足倍数关系。
拼接点处的前后2段曲线sfront(u1)和sback(u2)的一阶导数和二阶导数满足如下关系:将(15)式展开化简并结合其在拼接点处二阶导数满足倍数关系可以得到:
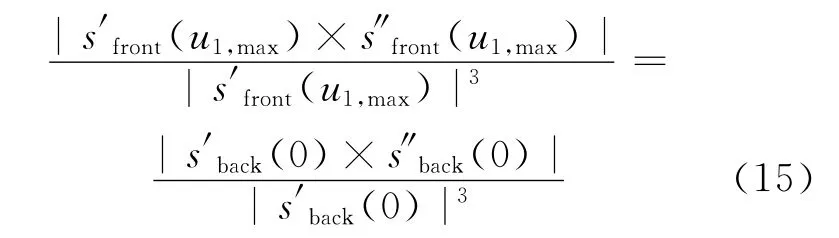
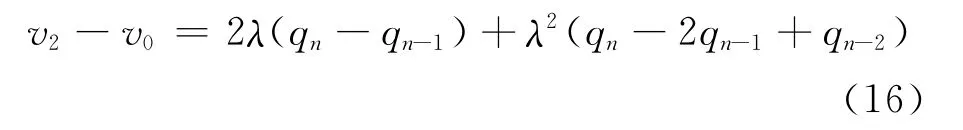
也就是说qn-2、qn-1、qn(=v0)、v1、v25点共面。
分段光顺拟合,首先要考虑的是对给定的点列进行分组,以分段处理。设给定数据点数为n,需拟合为m次曲线(m<n),则每组的数据点数应不少于m+2个,不然将得到一条完全插值于给定点的曲线。首先从数据点列中取出m+2个点作为第1组,并将第1组的最后一个数据点作为下一段的起始点,记第i个数据点分组内的第j个点为pi,j,第i组内的数据点数为si,则j=0,1,…,si。计算分组连接点与前后数据点所构成向量之间的夹角及连接点到其前后数据点所构成的直线段的距离,保证在连接点处不会出现曲线振动较大的情形,如图1所示。给定夹角与距离的范围(本文给定为夹角0°~90°,距离选定为0到前后数据点所构成直线段长度的1/3),夹角与距离均在给定范围则以此点为连接点,否则判断下一点是否符合连接点标准,如图2所示。若剩下的点数小于m+2则并入上一组,若剩下的点数大于等于m+2且小于2m+4,则全部作为第2组。依次类推,对数据点列进行分组。
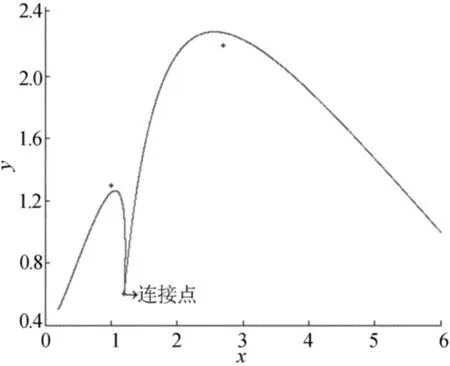
图1 连接点处曲线出现较大振动的情形
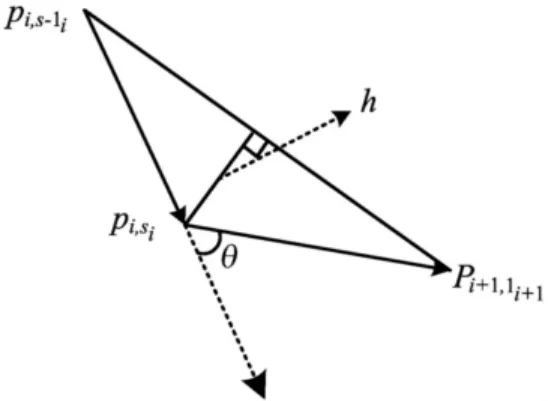
图2 连接点与前后数据点的向量构成
其中,图2中的θ为向量间的夹角;h为连接点到前后数据点所构成直线段的距离。
分段光顺拟合后,拼接点处可达到G1的具体算法如下:
(1)将数据点列按本节所述方法分组,记所分组列为ri(i=1,…,k),k为总组数。
(2)利用介绍的局部插值拟合方法拟合r1内的数据点列,使拟合曲线通过r1的首末数据点及其间所选定的若干(少于m-1个)数据点,得m次曲线c1。使用改进的光顺模型(8)式处理曲线c1,得光顺后的曲线c′1。
(3)拟合ri(i=2,…,k)内的数据点列,使得拟合的曲线通过ri的首末数据点及其间所选定的若干(少于m-1个)数据点,得到m次曲线ci。运用改进的光顺模型(12)式,对曲线ci做光顺处理,得到与前一段已光顺曲线光滑拼接的光顺曲线c′i。重复步骤(3),直到i=k。
按照上述步骤,边拟合边光顺,逐段进行,可以得到一条整体较为光滑且与所给数据点整体走势较为相符的曲线。
5 应用实例
以三次H-Bézier为例,对给定数据点分2段
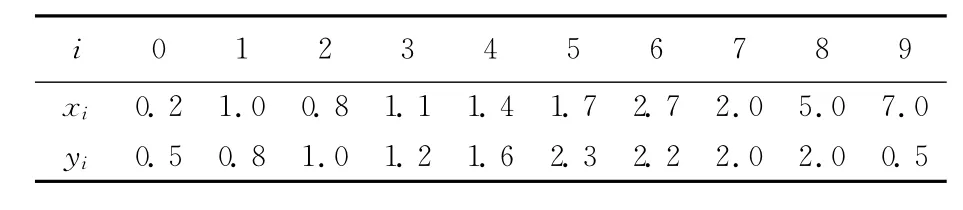
表1 数据点Pi(xi,yi)
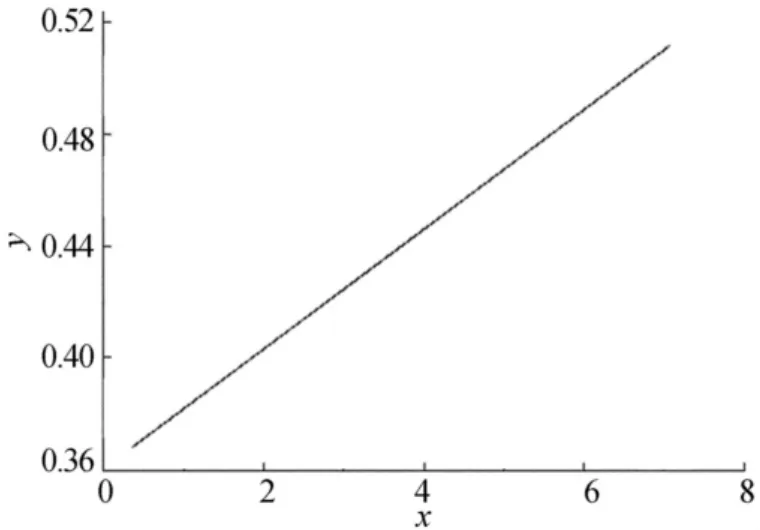
图3 文献[6]方法光顺后的曲线
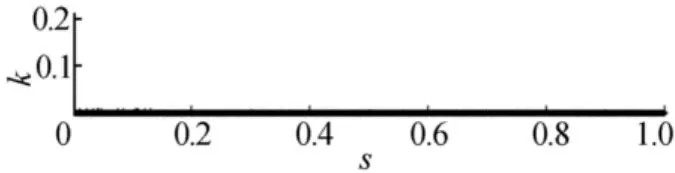
图4 文献[6]方法所得曲线曲率
曲线及曲率如图3~图9所示。处理,简单实现本文所提出的分段光顺拟合方法。光顺方程系数取a=2×10-3,b=3.9×10-1,c=2×10-3,光顺模型(12)式中的λ取1。给定一组数据点Pi(xi,yi),i=0,1,…,9,见表1所列。
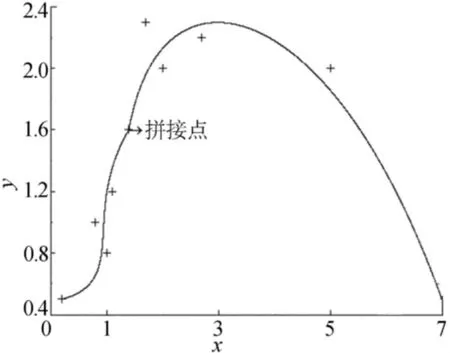
图5 未做处理前的拟合曲线拼接
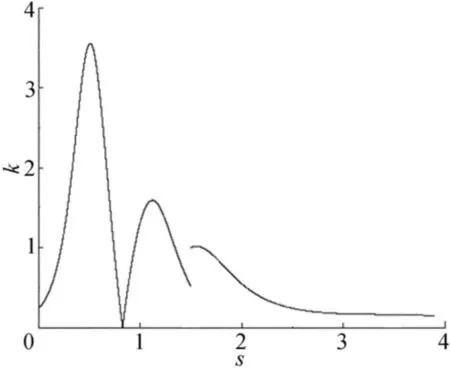
图6 光顺处理前曲线曲率
从图3可以看出,由于文献[6]方法仅与曲线应变能、应力能等有关,使得能量极小时所得曲线为直线。
尽管这时的曲线曲率极小(如图4所示),但所得结果已不再是一条包含形状变化的曲线,失去了应用价值,偏离了光顺的初衷。在文献[6]方法的基础上加入控制顶点变化范围的约束条件可以避免出现曲线直化的问题。在此,使用这种修正的方法与本文方法做对比。
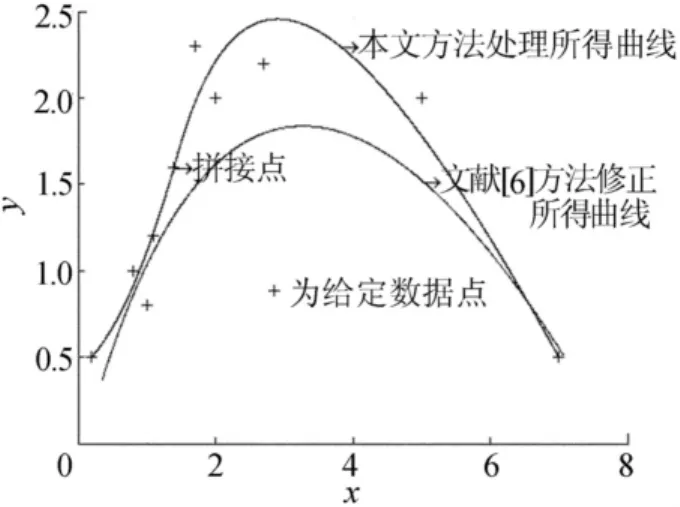
图7 本文所得曲线与文献[6]修正方法所得曲线
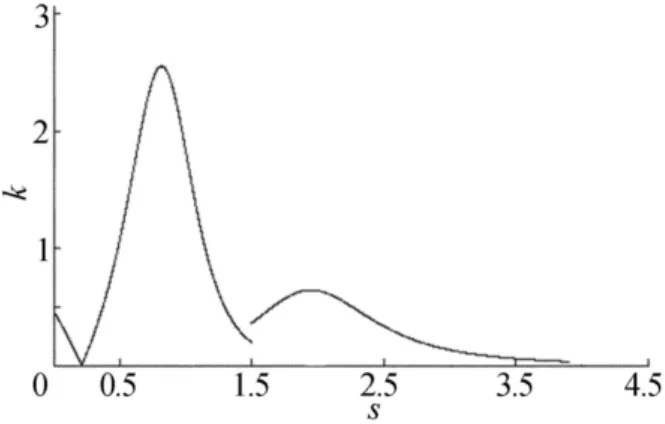
图8 本文方法所得曲线曲率
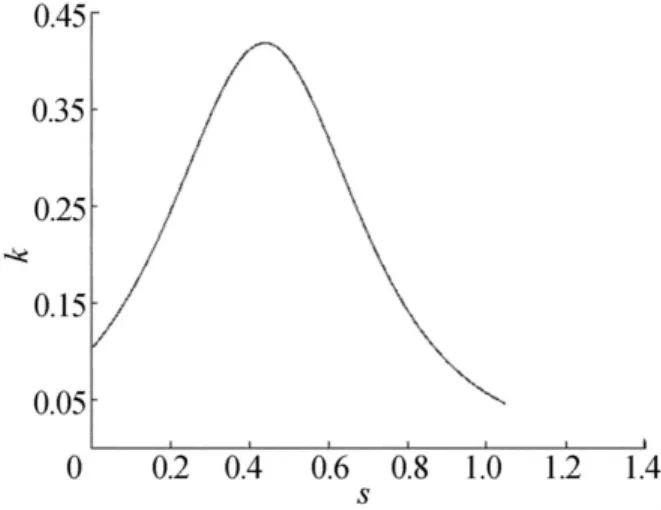
图9 文献[6]修正方法所得曲线曲率
由图5~图9可知,按照本文算法处理后的曲线整体走势与拟合拼接曲线基本相同,但处理后的曲线曲率比未处理曲线的曲率变化更小,曲率分布区间相对光顺处理前较小,达到了光顺的目的。
本文方法相对于修正的文献[6]方法更能准确反映给定数据点的走势,处理之后得到的曲线与给定数据点的偏差远小于文献[6]方法所得的曲线与给定数据点的偏差,见表2所列,且能插值于指定点,更能适应工业上对复杂器件外形设计时的需求。由于文献[6]所采用的光顺准则是能量法准则,光顺能愈小,曲率愈小,曲率变化区间变小,但由此带来曲线变化愈是趋于直线化的结果,失去了设计曲线应有的多样性。修正后的文献[6]方法虽然可以避免曲线直化的问题,但曲线仍不能够更准确地逼近数据点。
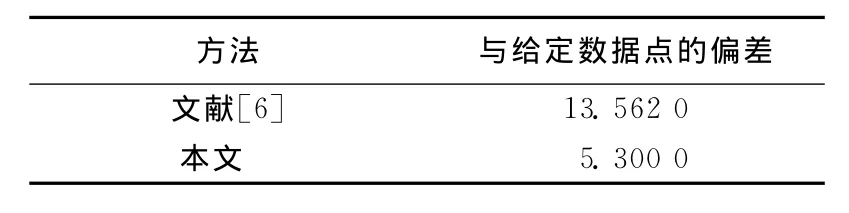
表2 光顺处理后曲线与给定数据点的偏差
注意到本文方法光顺后的曲线曲率图中有间断点,这是经过本文算法处理后,在拼接点处达到了G1连续,虽然这已经可以达到工业设计的要求,满足了人们对设计光滑曲线的需求,但并不能保证在拼接点处达到G2连续,因此会有中间断点的出现,这也是下一步要做的工作。
6 结束语
本文给出了分段光顺拟合给定数据点的算法,并给出了应用实例。通过实例可以看出,本文算法取得了一定效果,提供了一种新的有效的工程设计手段。本文算法在达到光顺效果的情况下尽可能地减小了计算量,且在曲线拼接处达到G1连续,可以满足工程应用的需要。对于要求在拼接处达到G2连续的需求,是下一步的研究方向。
[1]Renz W.Interactive smoothing of digitized point data[J].Computer Aided Geometric Design,1982,14 (5):267-269.
[2]Farin G,Rein G,Spapidis N,et al.Fairing cubic B-spline curves[J].Computer Aided Geometric Design,1987,4(1/2):91-103.
[3]Kjellander J A P.Smoothing of cubic parametric spline[J].Computer-Aided Design,1983,15(3):175-179.
[4]Spapidis N,Farin G.Automatic fairing algorithm for B-spline curves[J].Computer-Aided Design,1990,22(2):121-129.
[5]郑兴国,檀结庆,三次Bézier曲线的光顺[J].合肥工业大学学报:自然科学版,2005,28(1):109-112.
[6]Yang Yadi,Qin Xinqiang,Hu Gang,et al.Fairing and approximation algorithm of C-Bézier curves[J].Journal of Computer Applications,2008,28(12):3132-3134.
[7]沈海鸥,陈淑珍,孙晓安.曲线的二次有理Bézier曲线拟合[J].武汉大学学报:自然科学版,1997,43(1):119-123.
[8]Fl¨ory S,Hofer M.Constrained curve fitting on manifolds[J].Computer Aided Geometric Design,2006,23(1):17-44.
[9]王 媛.H-Bézier曲线的理论及其应用研究[D].西安:西北大学,2006.
[10]吴荣军.平面三次 H-Bézier曲线的形状分析[J].应用数学学报,2007,30(5):813-821.
[11]檀结庆,王 燕,李志明.三次 H-Bézier曲线的分割、拼接及其应用[J].计算机辅助设计与图形学学报,2009,21(5):584-588.
[12]Zhang Caiming,Zhang Pifu,Cheng Fuhua.Fairing spline curves and surfaces by minimizing energy[J].Computer-Aided Design,2001,33(13):913-923.
[13]苏步青,刘鼎元.计算几何[M].上海:上海科学出版社,1981:217-242.
[14]朱心雄.自由曲线曲面造型[M].北京:科学出版社,2000:206-365.
[15]Farin G,Sapidis N.Curvature and the fairness of curves and surfaces[J].Computer Graphics and Applications,1989,9(2):52-57.
Piecewise fairing and fitting of H-Bézier curves by partial interpolations
ZHANG Long-fei, TAN Jie-qing
(School of Mathematics,Hefei University of Technology,Hefei 230009,China)
This paper presents a new method of fairing and fitting based on partial interpolations,which can completely describe the distribution of the given data by piecewise fitting.An improved fairing method is also put forward.Once the fairing constraint equations are determined case by case,the fairing energy can reach the minimum level through adjusting the control points and choosing the suitable control parameters to get an ideal approximation of the given points.Numerical examples are given to show the effectiveness of the presented methods.
H-Bézier curve;piecewise fitting;fairing;energy method;curvature
TP391
A
1003-5060(2011)10-1570-06
10.3969/j.issn.1003-5060.2011.10.029
2011-04-22;
2011-06-20
国家自然科学基金资助项目(61070227;60773043);高等学校博士学科点专项科研基金资助项目(20070359014)
张龙飞(1986-),男,安徽萧县人,合肥工业大学硕士生;
檀结庆(1962-),男,安徽望江人,博士,合肥工业大学教授,博士生导师.
(责任编辑 朱华新)

