木糖醇玻璃焓松弛动力学的现象学研究
崔培培, 高 才, 杨 锁, 叶 斌, 唐景春, 倪宜华
(合肥工业大学 机械与汽车工程学院,安徽 合肥 230009)
玻璃态是热力学上的非平衡态,处于该状态的物质会经历一个自发的向同温度下平衡态趋近的连续过程,称之为结构松弛[1]。该过程中伴有过剩焓的释放,故也称焓松弛,这是一个非常缓慢的过程,有许多实验手段可用于研究这种现象,如DSC法、动态机械分析法(DMA)、介电法和热膨胀测定法等。DSC具有很高的测量精度且重复性好,是研究物质玻璃化转变和焓松弛行为的有力工具[1-7]。文献[1-2,8]结合该方法,采用Tool-Narayanaswamy-Moynihan (TNM ) 或AGV现象学模型对一些物质玻璃转变和焓松弛行为进行了研究。这2种模型均能很好地描述物质玻璃体系的焓松弛现象,但文献[5-8]发现,不同现象学模型对物质焓松弛行为预测效果往往存在差异。一些学者在原有模型的基础上作了改进,针对聚合物玻璃体系分析了不同现象学模型的预测力。文献[3-4]在AG协同松弛理论的基础上引入松弛极限态,建立了GR焓松弛模型,继而运用这2种模型拟合的参数与介电实验分析的结果作了对比[5];文献[6]在AG理论的基础上引入非线性参数xs,建立了H模型,并比较了H模型与TNM和AGV模型预测力大小[8];针对聚合物玻璃形成体系,文献[2]将AGV与改进的TNM多参数模型作了比较,并对GR与H模型的预测力进行了对照分析[7]。目前所有此类对比分析的文献都无一例外地针对聚合物系统,这些模型对除聚合物以外的玻璃形成系的预测能力的差异报道不多。
本文选择木糖醇作为模型系统,拟采用AGV、GR和H3种焓松弛现象学模型,结合DSC技术,比较3种模型描述小分子氢键玻璃形成系焓松弛行为时的预测能力。
1 数学模型
焓松弛是一个非线性和非指数性的过程,其非指数性质由Kohlrausch-Williams-Watts(KWW)延展指数函数描述,即
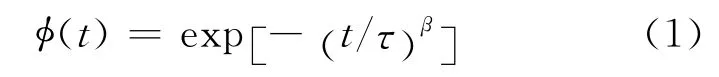
其中,φ(t)为松弛函数;τ为特征松弛时间;β(0<β≤1)为焓松弛过程非指数性质的无量纲量,用于表征松弛时间分布宽度。
焓松弛不仅依赖于温度变化,还与体系结构变化有关,Tool引入Tf作为玻璃化物质的结构参数。Scherer等基于AG理论,给出了AGV模型焓松弛时间的表达式为:

其中,A为指前因子,可看成物质在温度无限高时的松弛时间;B=ScΔμ/k,Sc为最小协同重排域的位形熵,Δμ为阻止单体(链段或分子)协同重排的能量势垒,是一个温度无关的量,k表示Boltzmann常数;R为气体常数;T2为Adam-Gibbs温度,表示位形熵消失时的温度。
文献[3]将位形熵Sc作为结构参数取代Tf,提出位形熵模型,其松弛时间表达式为:文献[4]引入松弛极限态假设,即GR模型。

文献[6]在玻璃化转变过程引入极限情况(即H模型),将玻璃化转变过程假设成2个相互独立的过程:①以玻璃化转变温度为Tf′时的极慢降温过程(xs=0);②以玻璃化转变温度为Tf″时的极快降温过程(xs=1)。通过引入非线性参数xs(0<xs<1),将Sc表示成依赖于热力学温度T和极限假想温度Tf(Tf′与Tf″范围内某一值)2部分,即

2 实验部分
2.1 实验仪器及试剂
采用配备G-M二级制冷系统的DSC仪器(Pyris-Diamond,美国 Perkin-Elmer公司),标称最低温度193K,实测DSC内样品温度最低可达约203K(随室温变化1K左右)。DSC以金属铟(99.999%,Perkin-Elmer)和纯水(实验室自制二次蒸馏去离子水)做两点温度标定,标定范围为210~320K;以冰的融化潜热(333.88kJ/kg)进行单点焓尺度标定,标定速率10K/min。氮气(99.999%)气氛,流量约20mL/min并保持恒定。分析纯结晶态木糖醇(Sigma,上海君创生物科技有限公司进口分装,99%)未经进一步纯化直接使用。取样品8~10mg(精确到±0.01mg),置于标准液体铝皿中央并压盖密封。
2.2 实验过程
先将结晶态样品从室温以10K/min升温至410K充分熔融,然后降温至Tg(247K左右)以下。将玻璃态样品升温至加样温度(室温)后,以0.5K/min的降温速率降低至215K,待热流稳定后按如下温度程序采集数据:① 等温1min;② 以10K/min升温到310K;③ 等温1min。将降温速率由0.5K/min 分别改为1、2、5、10、20K/min,重复以上实验。取与样品皿质量相同的空皿(±0.01mg),骤冷至215K,热流稳定后,按与分析样品相同的温度程序获得基线热流,用于比定压热容计算。为了保证热接触状况的一致性,针对样品的所有分析结束后再获得一条用于计算比定压热容的基线。
2.3 曲线拟合算法
本文对3个模型分别利用曲线拟合技术,采用曲线拟合程序以Matlab(附优化工具箱)语言编制。由于模型中各个参数之间存在很强的关联性,在对AGV模型进行曲线拟合时,不能对模型中4个参数同时进行拟合,故采用嵌套循环搜索,将T2置于外循环固定,搜索其他3个参数(A,B,β)的最优值。对GR和H模型采取同样的方法,将T2置于外循环分别搜索A,B,β,δ和A,B,β,xs。
现象学模型中参数值依赖于DSC扫描时的热历史,玻璃体系经历不同的热历史,模型的各参数值可能会有所不同[2]。但各现象学模型提出的初衷是寻求材料常数,即和玻璃体系所经历的热历史无关[1],模型参数拟合值与实验数据的一致程度是本文讨论模型预测力大小的重要标准之一。
文献[1,3]中用现象学模型对实验数据进行拟合时,只考虑单纯的评估模型参数与玻璃体系所经历的热历史之间的关系,没有考虑模型与实验数据之间拟合的均方差,为了更加精确地比较3种模型对实验数据的预测力,本文针对6次实验数据利用Nedler-Mead搜索方法寻求最优参数,使模型与实验数据之间拟合的均方差σa最小,即

其中,i为实验次数;j为实验扫描时的温度点;w(i)为由峰高确定的权重因子(0<w(i)<1)。
3 结果与讨论
3.1 模型参数
文献[1-9]表明,利用现象学模型对实验数据进行非线性曲线拟合获得模型参数时,模型参数的初值选取尤其重要,不同的初始值可能会导致不同的搜索结果。
本文在对木糖醇实验数据拟合之前,首先取升降温速率为10K/min,根据松弛时间τ≈100s时的玻璃化转变情况来估算指前因子A,采用文献[1]中DSC法测定的木糖醇玻璃化转变温度Tg(取247.5K),AGV与TNM模型参数之间的关系式[1]为:
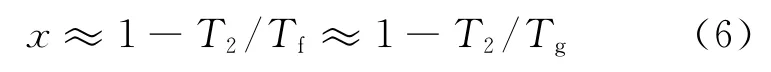
从文献[2]中获得(6)式中非线性参数x值,可估算AGV模型参数T2≈149K。Williams等采用黏弹性实验,结合 WLF方程分析得出大多数玻璃化物质Tg-T2≈50K。结合这2种方法,设定可变参数 T2为127.5 ~197.5K,搜索AGV模型中其他3个参数的值,见表1所列。
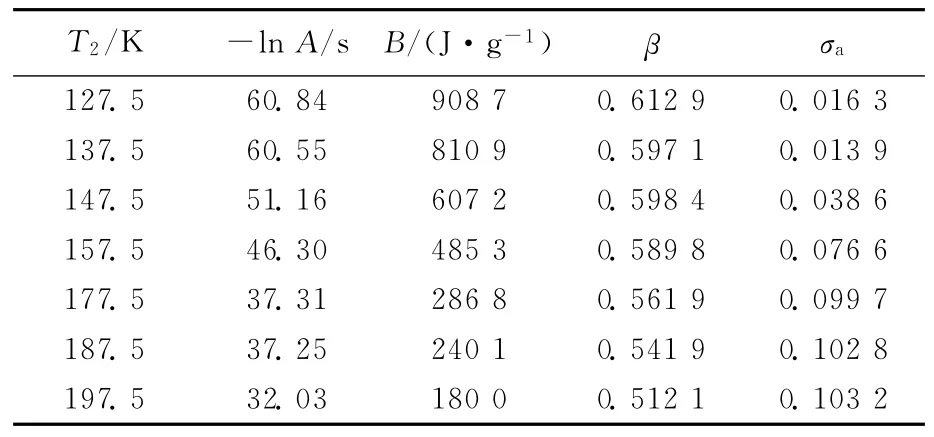
表1 设定不同的T2值AGV模型对木糖醇实验的拟合参数
由表1可以看出,随着T2的增加,指前因子A呈增加趋势,而非指数性质β与B均呈现出总体减小的趋势,和已报道的聚合物[2,6]变化趋势相同,但拟合的非指数性质β值较TNM模型[1]拟合值小。木糖醇在不同降温速率下实验比定压热容(散点)与GR模型拟合(实线)最好时的结果对照(T2=137.5K)如图1所示,模型各参数拟合结果见表2所列。
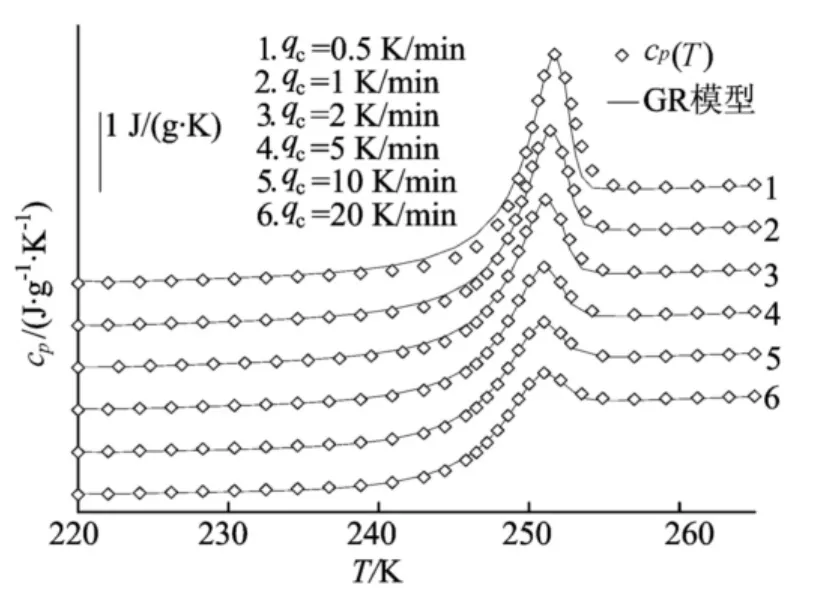
图1 木糖醇实验cp(T)与GR模型拟合结果
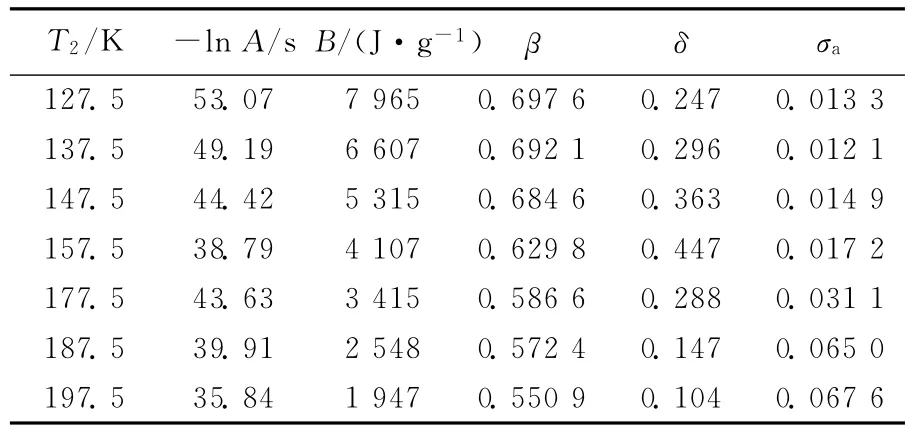
表2 设定不同的T2值GR模型对木糖醇实验的拟合参数
从图1可以看出,GR模型可以很好地重现6种不同降温速率的DSC实验数据。
由表2可以看出,随着T2取值的增加,GR模型加入新参数δ的值并没有呈现规律性变化,而是在一定范围内(0.1~0.44J/(g·K))波动,是木糖醇玻璃化转变过程中比定压热容增量(Δcp(Tg)≈0.96J/(g·K))[1]的10%~45%。δ在木糖醇中所表现的性质与已报道聚合物结果有一定的差异,文献[3-4]发现一些聚合物δ的值是其玻璃化转变过程中比热容增量的45%左右,说明木糖醇玻璃体系存在的假设亚稳极限态比聚合物更加趋近它们各自对应温度下的平衡态。木糖醇在不同降温速率下实验数据无量纲比定压热容(散点)与H模型拟合(实线)最好时的结果对照(T2=157.5K)如图2所示,模型各参数拟合值见表3所列。

图2 木糖醇实验cp(T)与H模型拟合结果

表3 设定不同的T2值H模型对木糖醇实验的拟合参数
H模型对木糖醇实验数据拟合结果显示,随着T2值的增加,新参数xs值增加明显,和聚甲基丙烯酸甲酯[7]xs值表现趋势相同,但木糖醇玻璃体系的xs值(0.035<xs<0.18)变化幅度远大于PAMM中xs值(0.02<xs<0.08)。同时,由TNM模型参数[1]和H模型参数的近似关系式[6]获得xs值为0.03~0.34。
3个模型同时对木糖醇实验数据进行曲线拟合,对比表1~表3发现,随着T2值的增加,3个模型得出的指前因子A均呈增加趋势,而非指数性质β与B均呈现出总体减小的趋势。但GR模型得出的指前因子A值较其他2个模型变化幅度要小,且由GR和H模型拟合的非指数性质β明显高于AGV模型拟合结果,同时也高于TNM模型[1]拟合的β值,这表明GR和H模型对位形熵模型改进时,在模型中引入新参数对其他模型参数有一定的影响。
3.2 均方差σa
由表1~表3可看出,AGV和GR 2种模型拟合的T2值一致表现在137.5K时(Tg-T2≈110K)σa最小,而H模型拟合的T2值在157.5K时(Tg-T2≈90K)σa达到最小,表明模型拟合与实验数据的一致性最好,但这不切实际,与 WLF方程分析得出大多数玻璃化物质Tg-T2≈50K相差甚远,类似的情况在聚合物[1,7-8]的研究中也有显现。
对AGV模型而言,随着T2取值的继续增大,σa呈现明显增大的趋势,对实验数据拟合效果表现不理想。GR和H模型表现出相同的变化趋势,但这2种模型对实验数据拟合的σa与AGV模型相比总体上有所减小,在T2取值较小时,GR模型对AGV模型改善较大,随着T2的增大,H模型对AGV改善效果较GR模型明显。
同时可以看出,3种模型在对实验数据拟合结果最好时,σa值变化不大,3种模型对实验数据的拟合效果相当。如以σa最小时的拟合结果作为模型参数的预测值,H模型预测的T2(T2=157.5K)明显高于前2种模型对T2值(T2=137.5K)的预测,且随着T2的继续增大,H模型对实验数据拟合的σa仍然较前2种模型表现理想。从模型与实验数据拟合的σa总体改善情况讨论模型预测力,H模型对实验数据的预测力较AGV模型和GR模型有了一定提高。
由表3可以发现,T2值从157.5K拟合效果最好结果开始继续增大到187.5K,σa仍然表现理想,以此值作为H模型对T2的预测,可以发现这一结果和介电松弛实验通过Vogel-Tammann-Fulcher(VTF)方程计算得到的木糖醇T2值[9](190±5)K结果一致。
结合介电法测得的结果,选择T2=187.5K,由表1~表3中的σa可知,H模型和GR模型对实验数据的预测力较AGV模型分别提高了约36%和80%。
3.3 Adam-Gibbs温度T2
通过现象学模型对实验数据进行曲线拟合,拟合出不同温度下焓松弛时间,对合理选择贮藏条件及延长货架寿命有一定的理论指导价值。在比较3种现象学模型对实验数据拟合情况时,有必要考虑不同现象学模型在选择相同T2值时,它们对松弛时间计算结果有无影响,3种现象学模型在T2=197.5K时,Tg附近焓松弛时间计算结果如图3所示。
由图3可以看出,在靠近玻璃化转变温度Tg时,3种模型对松弛时间的拟合结果比较一致,随着T相对于Tg偏离距离的增大,3种模型计算出的松弛时间出现一定差异,在T为225K时,H模型计算出的松弛时间是AGV模型和GR模型计算出松弛时间的3倍。另外,在计算过程中发现,对于同一种模型而言,T2选取在一定范围内计算出体系的松弛时间表现出很好的一致性(其他T2值计算结果和图示几乎重合,为清晰起见未在图中标出),和苯乙烯-丙烯腈共聚物表现出的结果类似[5]。所以,在木糖醇玻璃体系中,这3种模型对T2值预测的准确性关系到模型对实验数据预测能力。
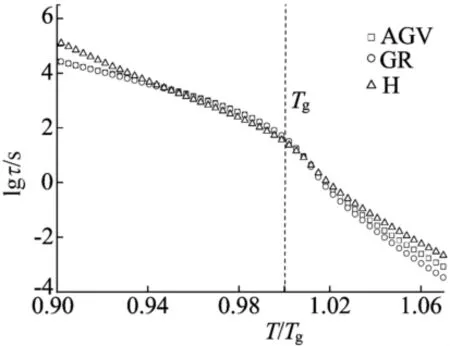
图3 3种模型计算木糖醇的松弛时间
AGV、GR和H模型均为基于AG理论的位形熵焓松弛现象学模型,GR和H模型又同时是对位形熵模型的非线性部分的改进。已有文献[6]表明一些模型对应参数之间具有一定的近似关系,由(6)式发现,T2值的大小和现象学模型的非线性程度有关,即非线性程度越大,T2值反而越小,如以拟合σa最小时结果作为模型参数,则发现3种模型预测的T2普遍小于由其他实验方法(介电松弛法、WLF方程分析等)分析得到的T2,AGV和GR模型拟合的Tg-T2的差值甚至高达110K左右,文献[6-8]在利用AG理论模型对聚合物玻璃体系焓松弛分析时也发现和木糖醇相同的结果。
采用位形熵模型对实验数据进行拟合过程中,Sc不完全取决于影响非线性性质的结构参数Tf[9],为了补偿位形熵理论中的非线性,H模型改进过程中添加更多的表征非线性特征的参数,对木糖醇玻璃系而言,将Tg-T2的差值降至90K,对实验数据拟合有了一定的提高。
用现象学模型对实验数据进行曲线拟合时,比定压热容增量Δcp(T)的处理方式对T2的结果也有一定的影响,Δcp(T)取常数或曲线表达形式时,基于AG理论的现象学模型松弛时间趋近于无穷大得到的T2值和Kauzmann温度(TK)相等[6]。文献[10]对T2和TK之间的关系也作了研究,并通过介电数据和比热频谱TK和T2之间的关系,发现在小分子有机物T2≈TK-20K。以拟合σa最小时结果作为模型的参数,在木糖醇中运用Dixon方法,可将H模型预测的T2值升至177.5K,与其他实验方法分析得到的结果接近。
对木糖醇而言,H模型引入xs将物质的玻璃化过程设想成2种极限过程,从热力学方面看有些不切实际。但物质在降温过程中,玻璃体系在玻璃化转变温度Tg附近会发生一个纯动力学过程,文献[11]发现在玻璃形成体系中有动力学非均质特性存在。另外,Glotzer通过数值分析研究发现在Lennard-Jones系统中快速域和缓慢域是可以共存的。将木糖醇玻璃体系焓松弛过程描述成快速和缓慢2个过程的综合,可使模型对实验数据的预测有一定的提高,表明H模型对木糖醇体系的焓松弛行为的描述更加成功。
4 结 论
运用AGV、GR和H 3种模型,结合DSC实验考察木糖醇玻璃体系的焓松弛行为,进行了模型预测力的分析。结果表明:
(1)3种模型均能很好地重现木糖醇经历不同热历史玻璃体系的升温cp曲线。
(2)3种模型预测的T2值普遍小于其他实验方法分析(如 WLF方程分析、介电松弛等)得到的结果。
(3)从现象学模型对实验数据拟合的均方差和模型对T2预测能力分析发现,H模型对实验数据的预测力优于AGV和GR模型。
[1]高 才,杨 锁,刘向农,等.木糖醇玻璃焓松弛的量热分析[J].物理化学学报,2010,26(1):7-12.
[2]Andreozzi L,Faetti M,Giordano M,et al.Enthalpy relaxation in polymers:a comparison among different multiparameter approaches extending the TNM/AGV model[J].Mac-romolecules,2003,36:7379-7387.
[3]Ribelles G J L,Pradas M M.Structural relaxation of glassforming polymers based on an equation for configurational entropy:1,DSC experiments on polycarbonate[J].Macromolecules,1995,28:5867-5877.
[4]Ribelles G J L,Pradas M M,Vidaurre Garayo A,et al.Structural relaxation of glass-forming polymers based on an equation for configurational entropy:3,on attained at infinite time in the relaxation process results on imide[J].Polymer,1997,38:963-969.
[5]Due˜nas J M M.Structural relaxation of glass-forming polymers based on an equation for configurational entropy:4,structural relaxation in styrene-acrylonitrile copolymer[J].Polymer,1997,35:2201-2217.
[6]Hutchinson J M.Application of the Adam-Gibbs equation to the non-equilibrium glassy state [J].Macromolecules,2000,33:5252-5262.
[7]Andreozzi L,Faetti M,Zulli F,et al.Enthalpy relaxation of polymers:comparing the predictive power of two configura-tional entropy models extending the AGV approach[J].Eur Phys J B,2004,41:383-393.
[8]Hutchinson J M,Montserrat S,Calventus Y,et al.On the application of the Adam-Gibbs equation to the non-equilibrium glassy state [J].Non-Cryst Solids,2002,307(310):412-416.
[9]Wehn R,Lunkenheimer P,Loidl A.Broadband dielectric spectroscopy and aging of glass formers[J].Non-Cryst Solids,2007,353:3862-3870.
[10]Dixon P.Specific-heat spectroscopy and dielectric susceptibility measurements of salol at the glass transition [J].Phys Rev B,1990,42:8179-8186.
[11]Ferguson A,Chakraborty B.Spatially heterogenous dynamics in dense,driven granular flows[J].EPL,2007,78(2):28003.doi:10.1209/0295-5075/78/28003.

