超越对数生产函数的半参数变系数估计模型

章上峰，顾文涛

（浙江工商大学 数量经济研究所，浙江 杭州 310018）

超越对数生产函数的半参数变系数估计模型

章上峰，顾文涛

（浙江工商大学 数量经济研究所，浙江 杭州 310018）

提出超越对数生产函数的半参数变系数模型，利用Profile方法给出产出弹性函数系数的局部加权最小二乘估计，并利用非参数条件自助法对有限样本的近似分布进行模拟，给出相对精确的广义似然比检验。规模报酬约束下中国1953—2008年的实证结果拒绝超越对数生产函数模型假设，产出弹性不可简单线性化而是对数劳均资本的非线性函数，时变资本弹性表现为倒U型变化趋势，时变劳动力弹性表现为U型变化趋势。

超越对数生产函数；半参数变系数模型；局部线性估计；广义似然比检验；自助法

一、引 言

生产函数模型是描述生产过程中投入的生产要素的某种组合与它可能的最大产出之间依存关系的数学表达式：其中Y为产出量，A、K和L分别为技术、资本和劳动力投入要素。美国数学家Charles Cobb和经济学家Paul Douglas导出的Cobb－Douglas（C－D）生产函数由于结构简单、经济意义明显，故应用最为广泛：

C－D生产函数模型具有明确的参数意义，At表示全要素生产率，α和β分别代表资本和劳动力的产出弹性，α＋β代表规模报酬，α＋β＞1表示规模报酬递增，α＋β＝1表示规模报酬不变，α＋β＜1表示规模报酬递减。

但是C－D生产函数模型假定服从中性技术进步，即资本和劳动力的产出弹性α和β是固定常数。但是，真正的常参数模型只存在于假设之中［1］32－37；现实中，由于资本和劳动力的数量和价格是逐期变化的，因而资本和劳动力的产出弹性也应该是时变的［2－3］。同时，C－D生产函数模型不管研究对象、样本区间和样本观测值是什么，要素替代弹性都为1，这是与实际不尽相符的。

根据要素之间替代弹性性质的描述为线索，不变替代弹性生产函数（CES）和可变替代弹性生产函数（VES）不断放宽C－D生产函数模型替代弹性为1的假设条件，超越对数生产函数（Trans－Log）则是一个更具一般性的变替代弹性生产函数模型，即：

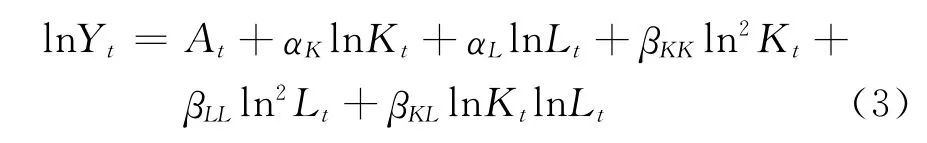
其中At、αK、αL、βKK、βLL、βKL为待定参数。容易证明，C－D生产函数模型和CES生产函数模型等都是超越对数生产函数模型的特例，当βKK＝βLL＝βKL＝0时，超越对数生产函数模型退化为C－D生产函数模型；当βKK＝βLL＝－1／2βKL时，超越对数生产函数模型退化为CES生产函数模型。此外，超越对数生产函数模型估计得到的资本产出弹性和劳动力产出弹性是时变的：

但是由式（3）可知，超越对数生产函数包含5个解释变量，且解释变量之间存在一定的相关性：如果进一步考虑技术水平替代变量，解释变量的个数可能会更多；如果解释变量或者待估参数过多，容易带来自由度不足、多重共线性等统计问题。同时，式（4）和式（5）表明资本和劳动力产出弹性分别是资本和劳动力投入量的对数线性组合函数，这一假设的合理性也有待确认。

非参数方法具有适应面广、可靠性强的特点，对模型的限制很少，特别适用于变量关系不确定的情况。但是，非参数回归模型可能存在样本要求高、外延难、经济意义不明显的问题。半参数模型与介于参数模型与非参数模型之间是一种适应面较广的模型；半参数模型保证模型对于实际产出的描述更接近实际，在提高模型解释能力的同时可解决模型误差较大的问题［4－5］。变系数模型是非参数模型的一种特殊情况，是经典线性回归模型的推广。笔者考虑结合半参数变系数模型的优点，给出如下形式的半参数变系数超越对数生产函数模型：

其中α（lnK t，lnLt）、β（lnK t，lnLt）是lnK t、lnLt的非参数光滑函数。对应资本和劳动力弹性估计值如下：

其中ρ1，ρ2非负，且满足ρ1＋ρ2＝1，则半参数变系数超越对数生产函数就退化为超越对数生产函数，因此它是一个更广泛和更具一般性的模型。

本文提出超越对数生产函数的半参数变系数估计模型，结合中国实例，利用Profile方法给出1953—2008年资本和劳动力产出弹性的局部加权最小二乘估计，并利用非参数条件自助法（bootstrap）对有限样本的近似分布进行模拟，给出相对精确的广义似然比检验结果。

二、模型设定与估计方法

假设技术水平At由一组可控制变量Z的线性组合表示：

其中Zi是衡量技术水平的各种不同指标，γi为未知参数，故有如下形式的生产函数模型：

其中α（lnK t，lnLt）、β（lnK t，lnLt）是lnK t、lnLt的光滑的未知系数函数，εt为随机扰动项。

模型（12）本质上是一种半参数变系数模型，变系数模型的优点之一是避免“维数灾难”，同时可以避免先验模型设定错误。半参数变系数模型常用的估计方法主要包括backfitting和Profile两种方法［6－7］。本文采用Fan和 Huang提出的Profile局部线性估计方法来估计未知参数和函数系数值。

假如｛（Zi，Ki，Li，Y i），i＝1，…，n｝是已经观测到的n个样本，对于给定的线性部分的系数γ，式（12）可以被写成：

这样式（12）就成为经典的变系数模型。

记u＝lnK，v＝lnL，则对于光滑的函数系数α（u，v）和β（u，v），采用局部多项式估计方法，在（u0，v0）处局部线性展开：

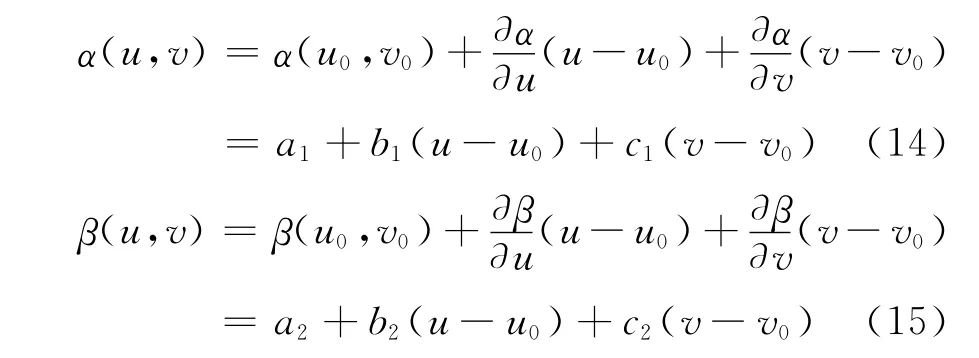
令X t1＝lnK t，X t2＝lnL t，故式（13）的估计问

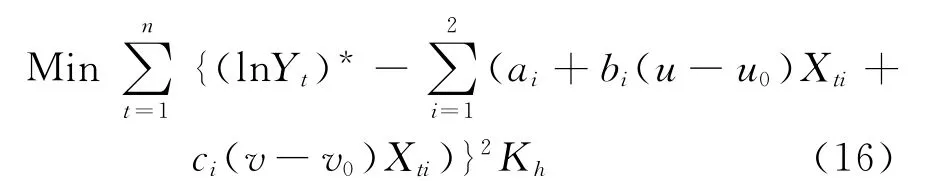
其中K h是个二元核函数乘上二维窗宽行列式的逆，一般可采用核函数比上窗宽的乘积：题就转化为局部加权最小二乘法来最小化：

一个感兴趣的问题是半参数变系数超越对数生产函数模型是否表现为经典的超越对数生产函数形式。由于非参数模型的复杂性，使得传统的基于极大似然估计的似然比（LR）检验无法实行，本文采用广义似然比（GLR）检验方法［8］，并通过条件自助法（conditional bootstrap）来确定统计量的p值。原假设H0为：

H0：经典超越对数生产函数模型成立 （22）

令超越对数生产函数为模型估计所得的残差平方和为RSS0，而半参数变系数超越对数生产函数模型估计所得的残差平方和为RSS1。广义似然比检验统计量为：

为了得到T统计量p值，采用如下算法估计：

第二，由上述的残差样本及下述公式产生相对应的lnY i的样本：

第三，对（（lnY）＊，lnK，lnL）用超越对数生产函数模型进行估计，从而得到T＊。

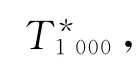
三、实证研究

数据说明如下：

1.国内生产总值Y（单位：亿元）。用以1952年为基期的实际国内生产总值表示。

2.资本存量K（单位：亿元）。1952年基期资本存量为807亿元，经济折旧率取9.6%［9］，法定残值率取4%［10］，以年初（上年年底）资本存量和年末资本存量的简单算术平均作为资本投入量，得到1953—2008年以1952年价格计算的中国固定资本存量投入量。

3.劳动力投入L（单位：万人）。以年初（上年年底）和年底就业人员数的平均值表示。以上数据来自《中国统计年鉴2009》、《中国国内生产总值核算历史资料》和《新中国五十五年统计资料汇编》。

实证研究中假设规模报酬不变，令：

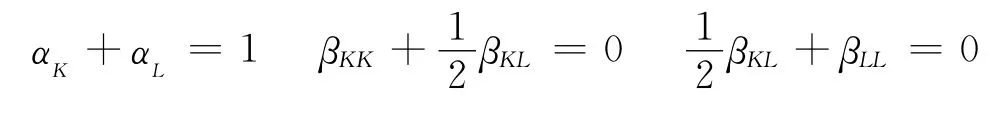
则规模报酬不变假设下的超越对数生产函数为：

其中y＝Y／L，k＝K／L，则资本产出弹性为：

在规模报酬不变假设下超越对数生产函数的半参数变系数模型为：

资本产出弹性为：

根据规模报酬不变假定劳动产出弹性为：

选取高斯核函数，根据交错鉴定法选取窗框，在规模报酬约束下利用Profile局部线性估计得到中国半参数变系数超越对数生产函数资本和劳动力产出弹性的估计结果（见表1）。

表1 半参数变系数超越对数生产函数产出弹性估计结果表

由表1可知资本产出弹性和劳动产出弹性在不同时期是时变的：（1）资本产出弹性从1953年的0.078逐步上升到1991年的0.485，此后呈现不断下降趋势，至2004年下降至0.255，2004年以后略微有所上升，变化范围在0.078～0.485之间，总体上呈现倒U型变化趋势。（2）劳动产出弹性从1953年的0.922逐步下降到1991年的0.515 5，此后呈现不断上升趋势，至2004年上升至0.745，2004年以后略微有所下降，变化范围在0.515～0.922之间，总体上呈现U型变化趋势，这个结果符合U型变化规律［12－13］。

以上研究结果进一步支持了产出弹性时变的研究结论［2－3，14－18］。为了更加直观地刻画资本和劳动力弹性的变化规律，本文给出超越对数生产函数（24）和半参数变系数超越对数生产函数（25）按对数劳均资本的排列趋势图（见图1）。

图1 资本、劳动力弹性按对数劳均资本变化趋势图

由图1可知：按照对数劳均资本排列的资本弹性和劳动力弹性也是可变的，但是不同于超越对数生产函数的简单线性结构（图1a），半参数变系数超越对数生产函数估计结果表明它们呈现和按时间系列相似的非线性变化趋势，即资本弹性表现为倒U型变化趋势、劳动弹性表现为U型变化趋势（图1b）。

广义似然比检验结果进一步确认以上研究结论，模型（24）残差平方和 RSS0为0.193 1，高于模型（26）残差平方和RSS1的0.143 1；广义似然比统计量T＝8.395 1，通过非参数条件自助法（conditional bootstrap）模拟得到统计量T的p值为0.027，从而拒绝原假设H0。因此，半参数变系数超越对数生产函数模型（26）是更为合适的一般化生产函数模型。

四、结 论

模型是对现实的模拟，模型总是建立在一定的假设基础上的，没有假设，就没有模型。而假设与现实之间是有差距的，这个差距越小，说明模型对现实的描述越准确。假设向现实的逼近，导致了模型的不断发展。生产函数模型是对生产活动中产出量与投入要素组合之间关系的模拟。C－D生产函数由于结构简单、经济意义明显而受到广泛应用。

虽然C－D生产函数模型假定服从中性技术进步，即资本和劳动力的产出弹性α和β是固定常数，但是真正的常参数模型只存在于假设之中；现实中由于资本和劳动力的数量和价格是逐期变化的，因而资本和劳动力的产出弹性也应该是时变的。此外，C－D生产函数模型不管研究对象、样本区间和样本观测值是什么，要素替代弹性都为1，这是与实际不尽相符的。根据要素之间替代弹性性质的描述为线索，不变替代弹性生产函数（CES）和可变替代弹性生产函数（VES）不断放宽C－D生产函数模型替代弹性为1的假设条件，超越对数生产函数（Trans－Log）则是一个更具一般性的变替代弹性生产函数模型。

作为一般性的变弹性生产函数模型，超越对数生产函数模型具有易估计和包容性等优点，但同时也存在参数个数过多、将产出弹性视作生产要素投入量的线性组合等问题。本文提出超越对数生产函数的半参数变系数模型，利用Profile局部线性估计方法，给出资本和劳动力产出弹性的局部加权最小二乘估计，并利用非参数条件自助法对有限样本的近似分布进行模拟，给出相对精确的广义似然比检验结果。规模报酬约束下中国1953—2008年的实证结果拒绝经典超越对数生产函数模型，产出弹性不可简单线性化而是对数劳均资本的非线性函数，时变资本弹性表现为倒U型变化趋势，时变劳动力弹性表现为U型变化趋势。

［1］ 李子奈，叶阿忠.高等计量经济学［M］.北京：清华大学出版社，2004.

［2］ 章上峰，许冰.时变弹性生产函数与全要素生产率［J］.经济学季刊，2009，8（2）.

［3］ 章上峰，许冰.初次分配中劳动报酬比重的测算方法研究［J］.统计研究，2010（8）.

［4］ 金剑，蒋萍.生产率增长测算的半参数估计方法：理论综述和相关探讨 ［J］.数量经济技术经济研究，2006（9）.

［5］ 许冰，章上峰.全要素生产率测算的半参数估计方法及其应用［J］.统计与信息论坛，2008（4）.

［6］ 花俊洲，吴冲锋，梅长林.一类半参数可变系数广义线性模型及其拟合［J］.统计研究，2003（12）.

［7］ Fan J，Huang T.Profile Likelihood Inferences on Semiparametric Varying－coefficient Partially Linear Models［J］.Bernoulli，2005，11（6）.

［8］ Fan J，et al.Generalized Likelihood Test Statistic and Wilks Phenomenon［J］.The annals of Statistics，2001（29）.

［9］ 张军，吴桂英，张吉鹏.中国省际物质资本存量估算：1952—2000［J］.经济研究，2004（10）.

［10］黄勇峰，任若恩，刘晓生.中国制造业资本存量永续盘存法估计［J］.经济学季刊，2002（2）.

［11］王小鲁，樊纲，刘鹏.中国经济增长方式转换和增长可持续性［J］.经济研究，2009（1）.

［12］许冰，章上峰.经济增长与收入分配不平等的倒U型多拐点测度研究［J］.数量经济技术经济研究，2010（2）.

［13］李稻葵，刘霖林，王红领.GDP中劳动份额演变的U型规律［J］.经济研究，2009（1）.

［14］Zhang S，Gu W.On Nonparametric Estimation for the Frontier Elasticity of Output with DEA Model［J］.Journal of Management Science ＆ Statistical Decision，2010，7（1）.

［15］许冰.外国直接投资对区域经济的产出效应——基于路径收敛设计的研究［J］.经济研究，2010（2）.

［16］章上峰，许冰，顾文涛.时变弹性生产函数模型统计学与经济学检验［J］.统计研究，2011（6）.

［17］高宇明，齐中英.基于时变参数的中国全要素生产率估计［J］.数量经济技术经济研究，2008（2）.

［18］罗羡华，杨振海，周勇.时变弹性系数生产函数的非参数估计［J］.系统工程理论与实践，2009（4）.

Semi－parametric Varying－Coefficient Estimation of the Trans－log Production Function

ZHANG Shang-feng，GU Wen-tao

（Institute of Quantitative Economics，Zhejiang Gongshang University，Hangzhou 310018，China）

This paper puts forward semi－parametric varying coefficient estimation for the Translog production function model.The function coefficients of output elasticity are estimated by profile least square method with the local polynomial estimates for the nonparametric part.Through the conditional bootstrap method，we use the GLR to test the Tanslog model against the semi－parametric varying coefficient model.Under constant returns to scale constraints，China＇s empirical results on 1953－2008 reject the null hypothesis of the Translog production function model，and the output elasticity is a nonlinear function of log capital per labor rather than a linear one.From our model，the time－varying elasticity of capital shows an inverted U－shape trend，and the time－varying elasticity of labor shows a U－shape trend.

translog production function；semi－parametric varying－coefficient model；local linear estimation；generalized likelihood ratio test；bootstrap

（责任编辑：郭诗梦）

F224.0

A

1007－3116（2011）08－0018－06

2010－12－17；修复日期：2011－05－04

国家社会科学基金青年项目《时变弹性生产函数：理论与应用研究》（09CTJ005）；国家自然科学基金项目《投资改变生产效率的识别与模拟：基于路径收敛设计研究》（70973110）；教育部人文社会科学基金青年项目《技术进步偏向与劳动收入份额变动：理论与中国实证》（10YJC790065）

章上峰，男，浙江温州人，统计学博士，助理研究员，研究方向：数量经济学、增长经济学与发展经济学；

顾文涛，男，浙江杭州人，理学博士，副教授，硕士生导师，研究方向：非参数统计。

【统计理论与方法】