运用增维的方法解决信息屏蔽问题

夏慧异

（1.上海财经大学 统计与管理学院，上海 200433；2.池州学院 数学计算机系，安徽 池州 247000）

运用增维的方法解决信息屏蔽问题

夏慧异1，2

（1.上海财经大学 统计与管理学院，上海 200433；2.池州学院 数学计算机系，安徽 池州 247000）

针对辛普森悖论、美国佛罗里达州的凶杀案分析中存在的矛盾以及基尼系数差异等问题进行了研究，研究认为：出现这些问题的根本原因是信息屏蔽造成的，提出用增加数据维数（简称为“增维”）的办法来解决这些问题中存在的信息屏蔽问题；运用增加维数的办法解释一些社会现象，可以使人们更加科学地看待一些问题，及时发现问题的原因，并找到相应的解决办法，为中国社会的科学发展服务。

数学模型；增维；信息屏蔽

一、引 言

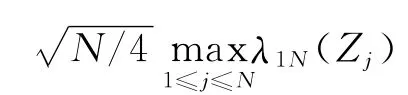
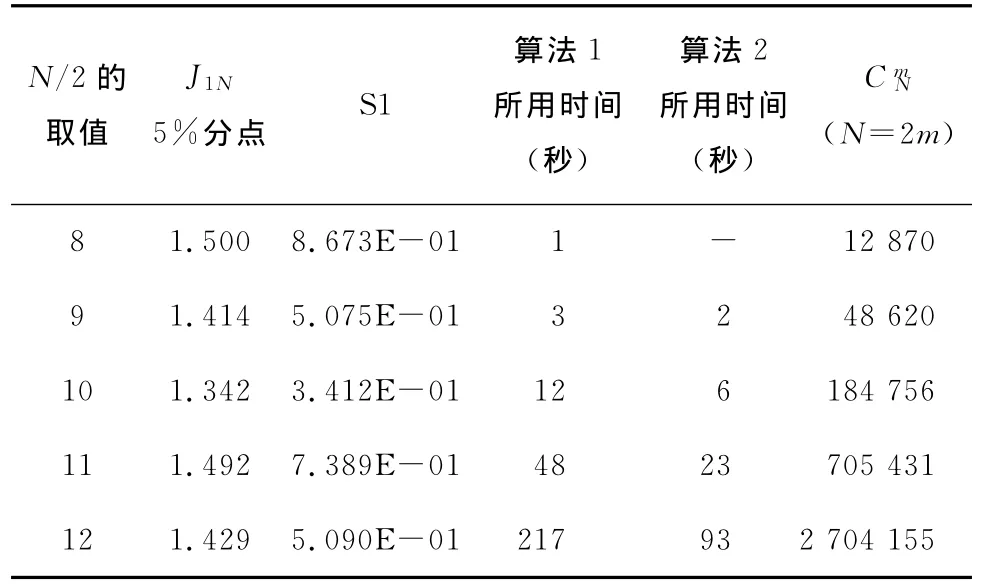
表1 J1N统计量两种算法所用时间的比较表

二、用增维的方法解决信息屏蔽问题

我们看看怎样用增加维数的办法解决美国佛罗里达州的凶杀案中326个死刑判决统计分析中存在的矛盾、辛普森悖论等问题。

美国统计学家对1976—1977年美国佛罗里达州的凶杀案中326个死刑判决案进行了研究［10］238－241，目的是研究美国法官有没有种族歧视倾向。在研究中得到两个数据表（表2和表3），统计学家对表2的数据进行了分析，数据显示美国法官没有种族歧视的倾向。对表3的数据进行了分析，数据显示美国法官有种族歧视的倾向。究竟是什么因素造成这种现象呢？

表2 被告肤色和死刑判决情况的分类表

相关研究很多，笔者从维数的观点对该问题进行了研究，并提出相应的数学模型。为建立数学模型，我们对影响死刑判决的相关因素进行假设，设死刑判决为随机变量X1，被告肤色为随机变量X2，被害人肤色为随机变量X3，在肤色上以0代表黑人，以1代表白人，在判决上以0代表没有被判死刑，以1代表被判死刑。将表2与表3分别变为表4与表5：

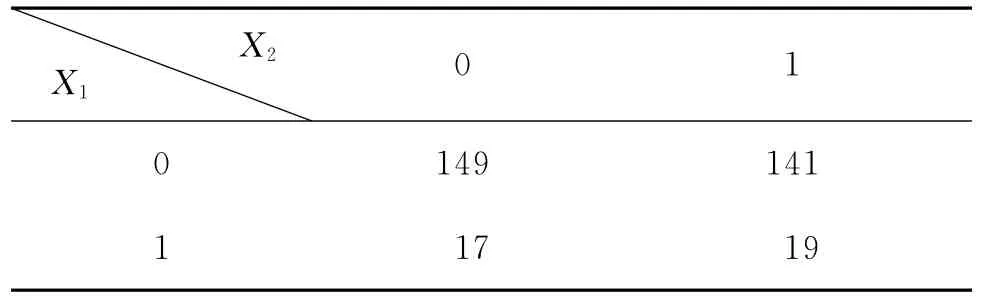
表4 被告肤色和死刑判决情况分类的数学模型表

相应的概率分布为：

表5 被告与被害人的肤色以及死刑判决情况分类的数学模型表

相应的概率分布为：

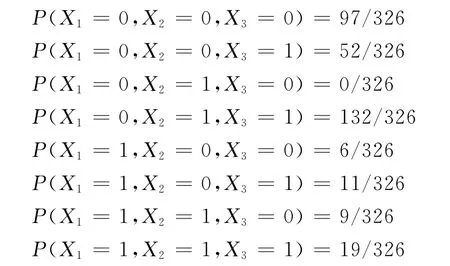
因为P（X1＝1，X2＝0）＝P（X1＝1，X2＝0，X3＝0）＋P（X1＝1，X2＝0，X3＝1），P（X1＝1，X2＝1）＝P（X1＝1，X2＝1，X3＝0）＋P（X1＝1，X2＝1，X3＝1），显然造成误判的原因是因为缺少随机变量X3所致，用二维（X1，X2）变量解释该问题时，所得结论与美国的社会现象不相符，这是缺少X3信息造成的信息屏蔽，我们用三维变量（X1，X2，X3）解释该问题时与社会实际情况相符。通过这个例子我们发现运用增维的方法可以解决这个问题。

当人们对两种变量的相关性进行研究时，有时会分别对其进行分组研究。辛普森悖论就属于这种研究，在某些前提下有时会产生的一种现象。即在分组比较中都占优势的一方，在总体评价中却并不占优势。该现象早在1899年由卡尔·皮尔森提出，但一直到1951年E.H.辛普森在论文中才正式解释了该现象，后来就以他的名字命名该悖论［7］。具体实验如下：为了比较两种药物（以下简称A、B）对某种疾病的治疗效果，临床观察了两批病人，每批40人，第一批中有30人服用A，10人服用B；第二批有10人服用A，30人服用B。疗效观测结果见表6。从表6中可见，第一批和第二批药物A优于药物B，但从二批综合统计上看，药物A劣于药物B，这样我们从相同的数据得到相反的结果，这类现象在统计学中称为辛普森悖论［5］。

表6 两组药物分组疗效和总体疗效表

为解决该问题，我们建立数学模型，设服用药物的人数为随机变量X1，设服用药物有效的人数为随机变量X2，设有效率为X3，显然X3＝X2／X1，我们在服用药物方面用0表示服用药物A，1表示服用药物B，在服用药物有效方面用0表示服用的药物无效，用1表示服用的药物有效，此时以上模型如表7所示：

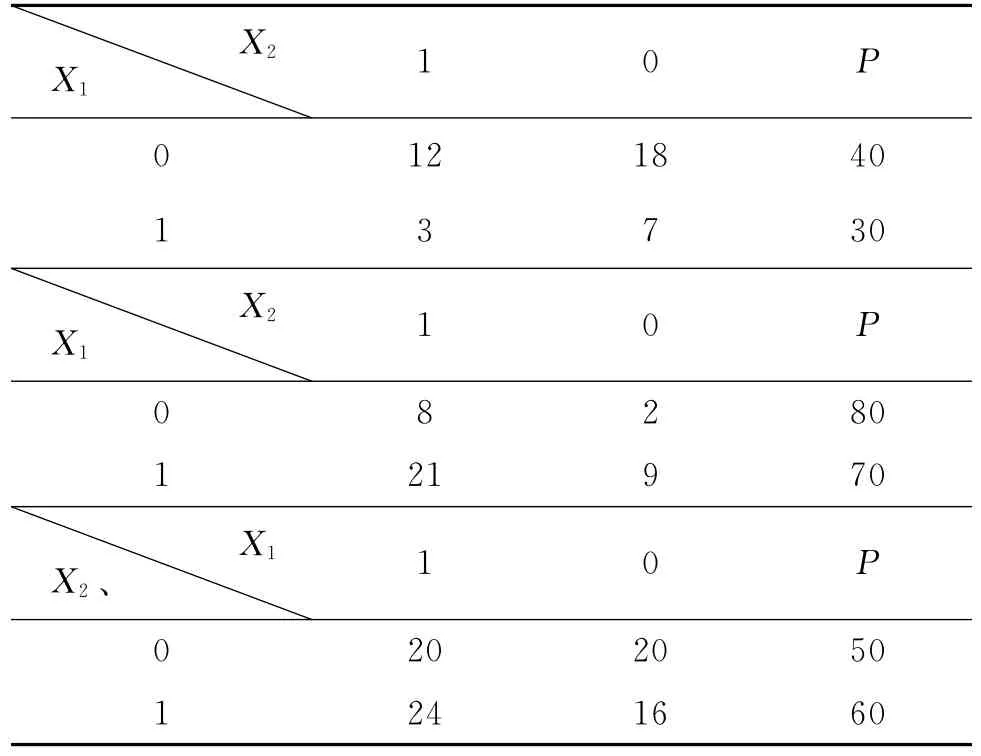
表7 两组药物分组疗效和总体疗效的数学模型表

通过分析我们发现造成误判的根本原因是应该用X1和X2来对问题进行评价，但我们用X3来评价，显然又是信息屏蔽造成的，对此我们可以用增加维数的方法加以解决。

三、现实意义

基尼系数是20世纪初意大利经济学家基尼提出的判断收入不平等的指标，国家统计局承认的2003年中国基尼系数为0.46［7］。联合国有关组织规定：基尼系数为0.4～0.5时表示收入差距较大。如果科学地看待这个问题时，我们发现造成这种差距的原因很多，第一个是区域差距问题。中国东部经济已经赶上发达国家，西部的发展程度和非洲差不多。第二个是历史原因造成的城乡差距。如果我们把这两个原因加进去，中国的收入差距没有基尼系数显示的那么大。中国目前正在进行西部大开发和城市化，这在将来会改变中国目前东、西部和城、乡收入差距过大的情况。运用增加维数的办法解释一些社会现象，可以使我们更加科学地看待一些问题，及时发现问题的原因并找到相应的解决办法，为中国社会的科学发展服务。

［1］ 滕树杰，张乃尧.分层模糊控制器的解析表达式及自适应控制方法［J］.清华大学学报：自然科学版，2002，42（9）.

［2］ 夏慧异，等.一种特殊函数的算法研究［J］.大学数学，2008，24（3）.

［3］ 沈萍.高维数据挖掘技术研究［J］.电脑知识与技术，2009（6）.

［4］ 胡洁.高维数据特征降维研究综述［J］.计算机应用研究，2008（9）.

［5］ 倪加勋.辛普森矛盾现象［J］.数理统计与管理，1992（1）.

［6］ 吴素萍，朱广萍.辛普森悖论（Simpson’s Paradox）和参数估计中的信息综合法［J］.宁夏农学院学报，2000（1）.

［7］ 王健，彭晓娟.辛普森悖论与利他行为的进化［J］.经济经纬，2008（5）.

［8］ 崔学海.基尼系数与中国的收入不平等［J］.重庆工商大学学报：社会科学版，2006（2）.

［9］ 胡志军，龚志民.收入基尼系数的统计推断［J］.统计研究，2010（9）.

［10］茆诗松，等.高等数理统计［M］.北京：高等教育出版社，2004.

Solving the Question of Information Shield by Method of Increasing Dimension

XIA Hui-yi1，2

（1.School of Statistics and Management，Shanghai University of Finance and Economics，Shanghai 200433，China；2.Department of Mathematics and Computer Science，Chizhou University，Chizhou 247000，China）

Simpson＇s paradox，conflict in statistical analysis of death sentences cases to murder in Florida and difference in the Gini coefficient has been studied in this paper.The root cause of these questions that caused by shields of information is pointed，the method of increasing the data dimension（refer to as“increase－dimensional”）is proposed for solving these questions.It may make us better look at some questions that some social phenomena is explained by the method.Allows us to discover the problem，find the appropriate solutions in time.It services to scientific development of our society.

model；increasing dimension；information shielding

（责任编辑：李 勤）

O213

A

1007－3116（2011）08－0015－03

2011－03－22

夏慧异，男，安徽郎溪人，博士生，副教授，研究方向：应用统计。

【统计应用研究】