线性回归模型设定的两个常见错误分析

刘 明

（兰州商学院 统计学院，甘肃 兰州 730020）

线性回归模型设定的两个常见错误分析

刘 明

（兰州商学院 统计学院，甘肃 兰州 730020）

删除截距项和遗漏解释变量是线性回归模型估计中的两个常见错误，删除截距项错误发生的原因是检验过程中发现其不显著而将其剔除，这会造成模型参数估计和假设检验的失真；遗漏解释变量的错误发生原因是人们错误认为只要变量存在相关性且存在因果联系就可以进行回归分析，以至于不考虑其它重要的解释变量，此时建立的模型不能用于经济结构分析和政策评价，最多只能用于预测目的。

设定错误；截距项；解释变量

一、问题的提出

线性回归模型是最基本的计量经济学模型，也是研究经济变量关系最常用的模型，它是经典计量经济学的主体内容，经典计量经济学就是围绕线性回归模型的设定、估计、检验和应用展开的。线性回归模型的参数估计、假设检验（包括统计检验和计量经济学检验）有着一套较为完备的统计学方法体系，只要对这一体系有所把握，在实际应用中就不会出现失误。根据研究对象和研究目的来构造回归模型并加以应用，事实证明，模型是否得到正确的应用往往取决于是否构造了一个良好的、正确的模型。对于线性回归模型的设定，是最容易出现错误、而且是最难以发现错误的环节，模型设定的正确与否，直接关系到建模的成败，一个设定错误，会使整个研究过程和研究结论都变得毫无意义和价值，因此需要仔细的斟酌研究。线性回归模型设定的常见错误主要包括：增加错误的解释变量，错误的模型数学关系式，删除截距项，遗漏重要的解释变量。增加了错误的解释变量可以通过t检验、F检验来诊断并发现该错误的变量，对于变量间数学关系式的选择，可以通过研究分析变量间的散点图来发现它们之间的关系，并通过拟合误差（例如均方误差、平均绝对误差等）来比较分析，选择正确的数学关系式的模型。本文的主要任务就是研究讨论删除截距项、遗漏重要解释变量这两类设定错误，分析它们的发生原因及后果，提出相应的解决办法，并讨论例外的情形。

二、删除截距项的线性回归模型

构建线性回归模型时可能出现这类情况：截距项的显著性t检验未能通过，即截距项的t检验结果支持其等于零的假定。此时截距项因为不显著而可能被删除。线性回归模型中的截距项通常不做经济意义解释，但这并不意味着截距项可有可无。如果在总体回归模型中应该包含截距项，删除后则会产生一系列不良后果。为简单起见，这里以一元线性回归模型为例对删除截距项所产生的后果进行讨论。

设正确的总体线性回归模型为：μi为随机干扰项，其满足高斯假定，设其方差为σ2。未删除截距项的样本回归模型表示为：

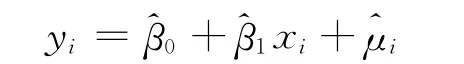
删除截距项的样本回归模型表示为：

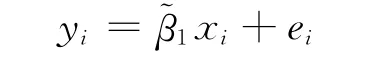
ei为样本模型的残差。设样本容量为n，则运用普通最小二乘法可得模型参数估计量：

首先分析该估计量的无偏性。

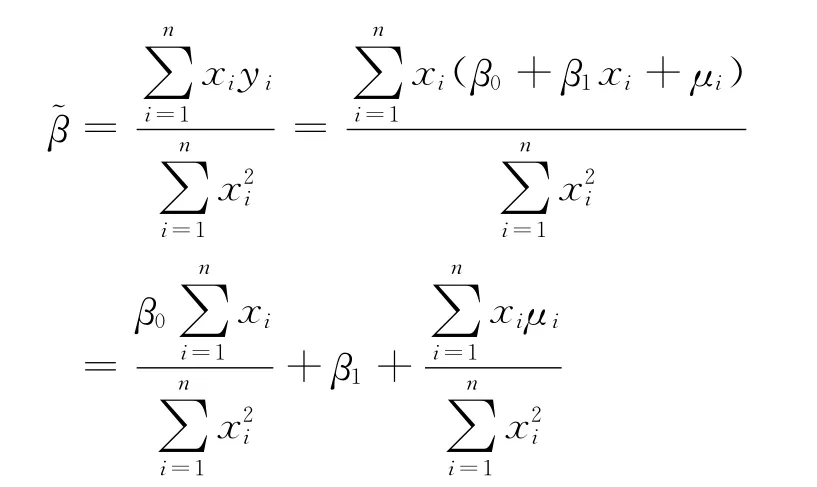
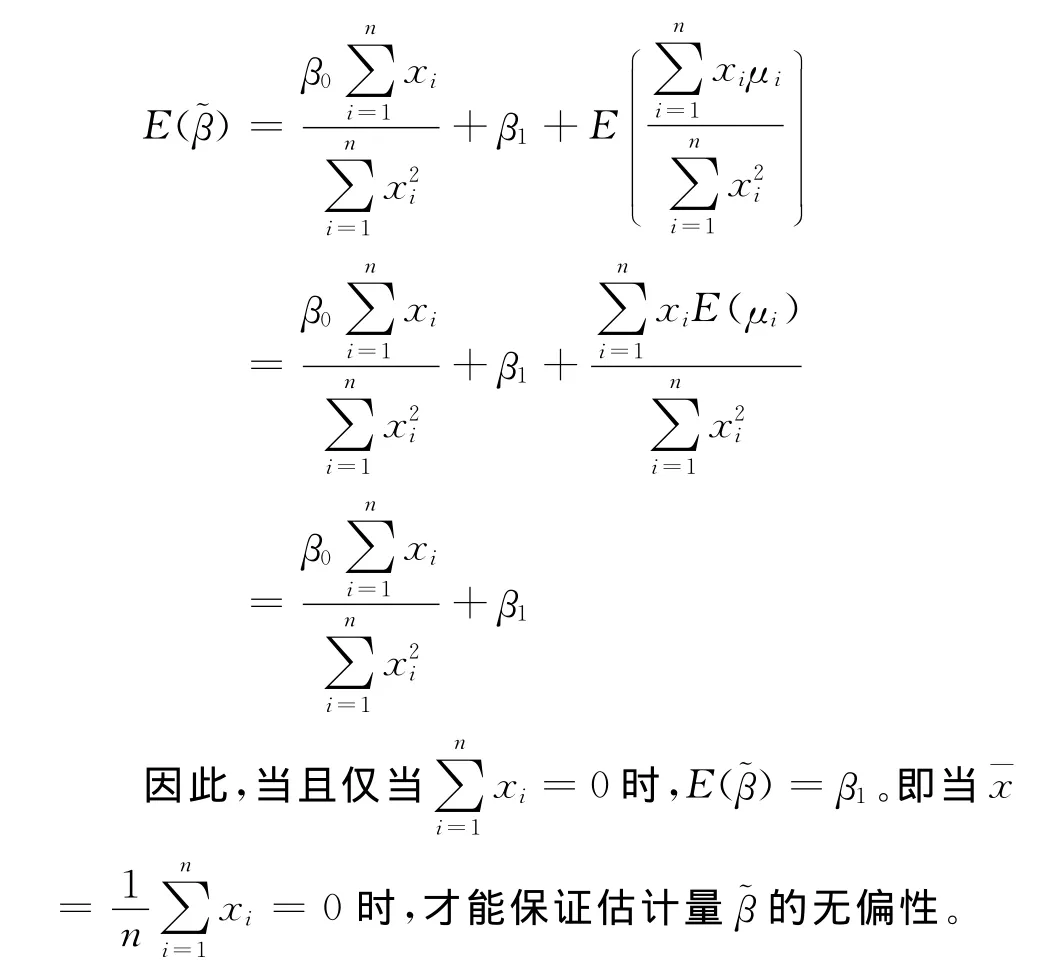
将此等式两边取期望，并根据高斯假定可得：再分析的方差。根据前述分析结果的方差为：

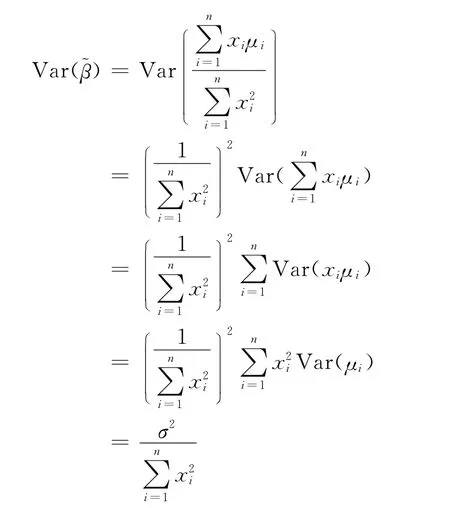
不难证明，未删除截距项的样本回归模型回归系数β1的普通最小二乘估计量为：

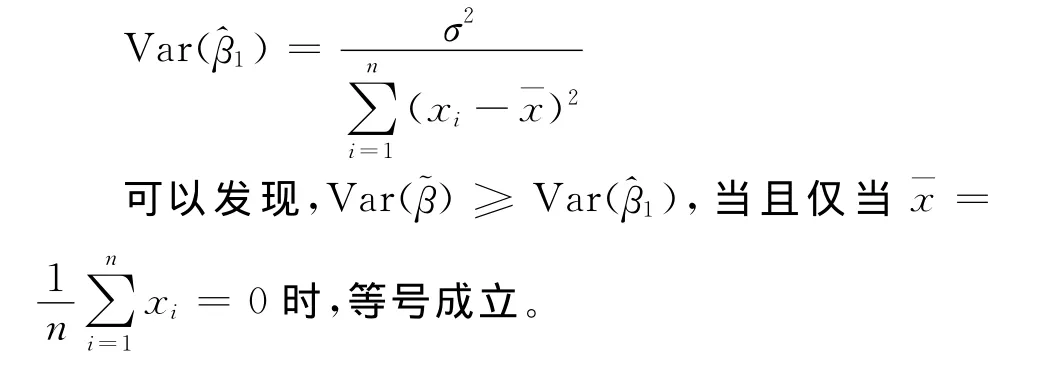
综上所述，当珚x≠0时，即便满足高斯假定，也无法保证估计量珓β的无偏性和最小方差性。

删除截距项的样本回归模型的残差之和为：

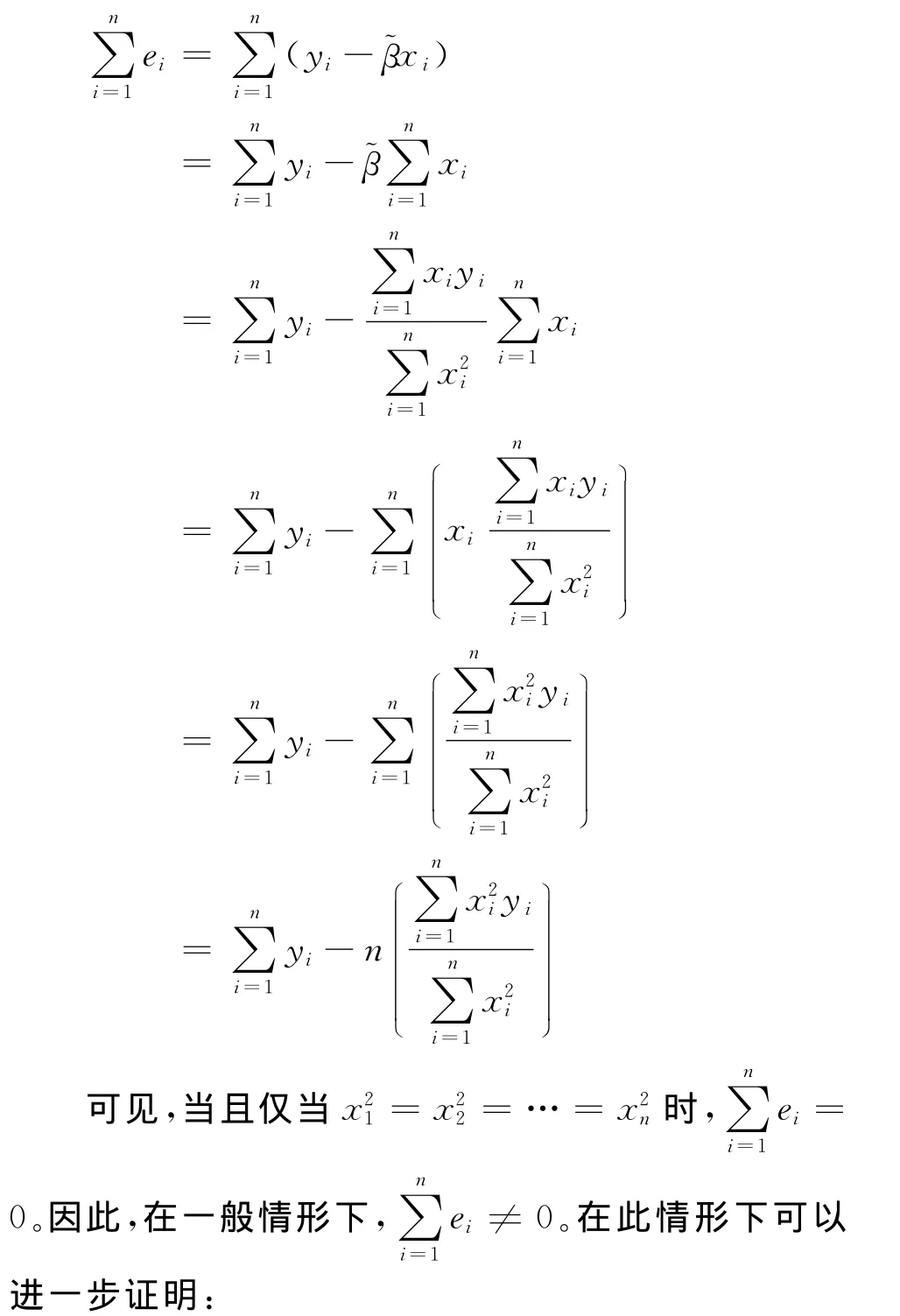
综合以上分析结论可以看出，在估计线性回归模型时一般需要包含截距项，即使t检验结论显示它是不显著的，剔除截距项仍须谨慎。事实上，线性回归模型中是否包含截距项是由总体特征决定的，即在设计、估计回归模型时要根据所研究总体的特征并结合经济理论来确定模型中是否应该包含截距项，如果没有理由表明模型不含有截距项，则在模型设定时须将其包含进来。

截距项的本质是线性回归模型的解释变量均值与被解释变量均值的线性组合：

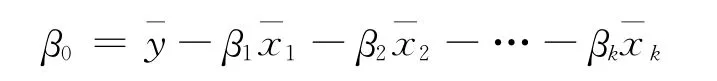
当理论上要求β0＝0时，则模型无须包含截距项。现实中存在不含有截距项的回归模型，在估计此类回归模型时便不能加入截距项了。常见的无截距项的线性回归模型有如下两类：

一类是解释变量和被解释变量的均值均为零的模型。例如使用标准化变量构建的线性回顾模型，标准化变量的均值为零，因此在构建回归模型时无须包含截距项；再如无水平趋势的平稳时间序列数据所构建的自回归模型，无论模型中的当前变量还是滞后变量，其均值都为零，因此也无须包含截距项。

另一类是差分模型。考虑回归模型（＊）及其一期滞后模型：

构造出差分模型为：

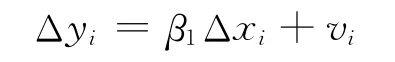
三、遗漏重要解释变量的线性回归模型

从理论上来说，反映变量之间关系的计量经济学模型是唯一的。对于线性回归模型而言，针对某个被解释变量，模型中应包含的解释变量是唯一确定的。具体说，在构建线性回归模型时，确定了被解释变量以后，模型中应该包含所有对该被解释变量有重要影响的解释变量，同时不能包含对该解释变量无重要影响的解释变量。在现实应用中，对于解释变量重要性的判断，不能仅依靠统计检验，也要结合经济理论和现实意义。对于模型中遗漏重要解释变量和包含不重要的解释变量所引起的后果［1］159－166，可参见文献［1］，本文不再做出讨论。

在线性回归模型的诸多设定错误类型中，遗漏重要解释变量是一个最常见的错误。长期以来，人们在研究变量之间关系的时候总是认为，只要变量之间具有相关性和某种经济联系（例如影响和被影响的因果关系），就可以利用这些变量构建回归模型，进行回归分析，这是片面的。依此思想建立的回归模型的解释变量和别解释变量虽然存在着相关性和影响作用，但模型中未必包含了所有的影响被解释变量的因素，此时的回归模型很可能是谬误回归。现举一例来说明这一问题。

笔者在研究中国经济增长问题时，选择了多个宏观经济指标，运用1990－2009年的数据，通过分析研究发现影响国内生产总值（GDP）的主要变量包括居民消费支出（REC）、政府财政支出（GC）、固定资产投资（INV）、进出口总额（TR），构建了如下的对数回归模型：

为节省篇幅，模型的检验指标数据未给出。由该模型可以看出，在其它条件不变的情况下，进出口总额每增加1个百分点，GDP平均增加0.04个百分点。

通过简单的分析就可以发现，这里GDP和进出口具有显著的相关性，而且进出口对GDP存在显著的影响，构造两者的对数回归模型：

ln（G＾DP）＝3.12＋0.79ln（TR）

按此模型的表述，当进出口总额每增加1个百分点，GDP平均增加0.79个百分点。这显然是不符合现实的，这个结论没有价值。

如何解决这类问题，以使得模型应包含所有的重要解释变量？这就要求在建模时遵循“由一般到简单”的原则，并坚持“唯一性”［2］。由一般到简单，即在建模型过程中考虑研究对象的一般性特征，充分考量研究对象系统内各经济因素的普遍联系，设计出尽可能反映出全面特征的一般性的回归模型，在此基础上进一步使用样本对研究对象进行考察。在经济理论和统计意义允许的情形下，可以将模型简化，用以反映研究对象的主要特征。唯一性，就是指反映经济变量间、经济系统特征的模型在理论上只有一个，不可能在同一时间、同一空间内并存多个正确的模型。坚持唯一性，本质上就是要求所建模型是最优模型。

利用线性回归模型进行经济结构分析和政策评价时，必须要求所建立的模型包含所有重要的解释变量、反映研究对象的一般性特征，否则可能会得出错误甚至荒谬的结论。而如果所构建的线性回归模型仅用于预测的目的，则上述要求可适当放宽。为说明这一问题，首先分析利用回归模型进行预测的条件。只要满足下述条件即可进行回归预测：（1）事物的发展变化过程是连贯式的，而非跳跃式的；（2）影响事物过去和现在发展变化的因素同样会影响到未来，且这些因素不会发生质的变化［3］5－6，67；（3）所涉及的变量之间具有显著的相关性，可以直接或进行变换后间接的建立线性回归模型。在满足这些条件时，可以建立变量间的线性回归模型，通过已知的解释变量预测未知的被解释变量。通过上述回归预测的条件可以看出，模型若仅用于预测目的，只需考察研究对象（预测目标）的某一个或一部分重要的影响因素，而不用全面的考察所有的影响因素以构建最优模型。原因有两点，一是研究对象的变动规律可以由某一个或一部分影响因素进行描述和解释，研究对象随着此类因素的变化而变化；二是可以将未包含在模型之内的其它变量看作是“影响事物发展变化的因素”，它支配着事物发展的过去和现在，依据预测条件，它同样支配着事物发展的未来，且不会发生质的变化。当然，为保证预测的精确性，要求所建立的回归模型通过各类统计检验和计量经济学检验。用于预测目的的时间序列变量的自回归模型就属于此类，它无需分析其它的影响因素，而只是根据自身的变动规律和特征构造回归模型，依此对未来进行预测；趋势外推模型亦属此类，它将研究对象对时间构造回归模型，而不考虑其它的影响因素。显然，这类模型只能用于预测，而不能进行经济结构分析和政策评价。

四、结论

线性回归模型的设定错误包括多种情形，本文研究分析了两类常见错误：删除截距项和遗漏重要的解释变量。

通过分析发现，当总体回归模型要求含有截距项而在设定模型时删除了截距项时，会产生一系列的严重后果，导致模型的估计结果和假设检验结论均失去可靠性。因此，一般情况下模型中应包含截距项，以使得回归模型符合参数估计和假设检验的要求。当然，不是任何回归模型都包含有截距项，现实中也存在不包含截距项的模型，差分模型和所有变量均值均为零的模型不应包含截距项。

正确反映变量间关系的模型在理论上只有一个，为能构建出最优模型，设计线性回归模型时要遵循“由一般到简单”原则和“唯一性”原则。总体回归模型的设定不能仅依据相关关系和因果关系，更要充分考虑影响研究对象的一般性因素，做到不遗漏解释变量。在线性回归模型设定过程中，如果仅用于预测目的，根据预测实现的前提条件，可以允许简化模型，选择少部分影响因素，将其余影响因素归于“支配事务发展变化的因素”，只要这些因素不发生质的变化，预测就可以顺利进行，只是此时的模型不能用于结构分析和政策评价的目的。

［1］ 李子奈.计量经济学［M］.北京：高等教育出版社，2000.

［2］ 李子奈.计量经济学应用研究的总体回归模型设定［J］.经济研究，2008（8）.

［3］ 徐国祥.统计预测和决策［M］.上海：上海财经大学出版社，2008.

Analysis on Two Common Errors Concerning Linear Regression Model Setting

LIU Ming

（School of Statistics，Lanzhou University of Finance and Economics，Lanzhou 730020，China）

Drop intercept and explanatory variables is two common errors in linear regression model setting.The cause of the former error is due to the inspection of the insignificance of the intercept and this will cause the model parameter estimation and hypothesis testing distortion；the cause of the latter error is that as long as the correlation between the variables exists，the regression analysis can be conducted without taking into account other important explanatory variables.Then the establishment of model cannot be used for economic structures analysis and policy evaluation，most can only be used for prediction purposes.

setting error；intercept；explanatory variables

（责任编辑：王南丰）

0212

A

1007－3116（2011）08－0011－04

2010－12－05

刘明，男，安徽霍邱人，讲师，经济学硕士，研究方向：经济计量分析。

【统计应用研究】