股指时间序列的分形插值模型与R／S分析

王宏勇，张青格

（南京财经大学 应用数学学院，江苏 南京 210046）

股指时间序列的分形插值模型与R／S分析

王宏勇，张青格

（南京财经大学 应用数学学院，江苏 南京 210046）

运用分形插值模型和R／S分析法研究股指时间序列的变化规律和结构特征，通过建立分形插值模型刻画上证综合指数在一定时间内的变化规律，并预测其在短期内的指数走势。使用R／S分析法和Hurst指数，分析了上证综指的结构特征，指出市场具有状态持续性和分形分布等统计特征。

分形插值；股指时间序列；R／S分析

一、引 言

股票价格的变化是极其复杂的，分形学的创始人Mandelbrot对股价的变化做了深入的研究，发现股票价格的变化曲线具有分形特征。Peters将混沌和分形统计的概念引入资本市场研究中，提出了分形市场假说，它突破了有效市场理论的独立、正态和线性等假设，为重新认识金融市场复杂的非线性本质特征提供了一个新的范式［1］39－85。分形 R／S分析法对揭示金融市场的长期记忆性、分形统计结构等特征提供了一个稳健的分析技术。黄诒蓉利用R／S分析法研究中国股票市场收益率序列的状态持续性［2］58－79。周洪涛等对上海股市的月、周、日收益率序列进行了研究，说明上海股市具有非线性特征［3］。申富饶等运用分形插值方法对股票的价格进行了分析和预测［4］。为了建立合理的分形插值模型对金融时间序列进行分析，本文在Mazel和Hayes研究的基础上提出了一种新的计算迭代函数系纵向尺度因子的方法，以此建立了一种仿射分形插值模型［5］。以上证综合指数为例，利用仿射分形插值模型模拟了股指序列的变化规律，预测了股指在短期内的变化趋势。最后运用R／S分析法和Hurst指数，分析了上证综合指数的分形结构特征。

二、分形插值模型的建立

设｛（x i，y i）∈R2：i＝0，1，…，N｝是一个给定的数据集，其中x0＜x1＜…＜x N。一个分形插值函数f：［x0，x N］→R是经过这个数据集的一个连续函数，其图像是某个迭代函数系的吸引子。由于在实际应用中使用最为广泛的是所谓的仿射分形插值函数，它是由仿射迭代函数系生成的。因此，本文主要考虑下列形式的迭代函数系｛R2：w i，i＝ 1，2，…，N｝，其中w i：［x0，x N］×R→R，i＝1，2，…，N为如下形式的仿射变换：

在式（1）中d i（i＝1，2，…，N）为自由参量，称为迭代函数系｛R2；w i，i＝1，2，…，N｝的纵向尺度因子，满足｜d i｜＜1。由式（1）和（2）可得：

满足条件（1）和（2）的迭代函数系｛R2；w i，i＝1，2，…，N｝称为仿射迭代函数系。由分形插值理论可知，该迭代函数系的吸引子是一个仿射分形插值函数f：［x0，x N］→R的图像［6］。

在仿射迭代函数系式（1）中，纵向尺度因子d i对分形插值函数的形态、性质等有着决定性的影响。如何合理地确定d i的值是建立仿射分形插值模型的关键。在利用仿射分形插值函数拟合实验数据或曲线的过程中，任给d i的值是没有意义的，这是因为使用任给的d i迭代产生出来的分形插值曲线很难较准确地拟合给定的d i数据或逼近给定的曲线。根据仿射变换式（1）和（3）可知，由给定数据点｛（x i，y i）：i＝1，2，…，N｝的信息，来确定d i的值是确定仿射迭代函数系的关键。对于离散数据集，Mazel和Hayes提出了计算d i的两种方法：几何法和解析法［5］。在几何法中，为了求得d i，必须先求出分形插值曲线到数据集两端点所成直线的最大纵向距离的点S（xs，ys）。由于S（x s，y s）仅为插值曲线上的点，未必是插值点，其位置通常难以确定。李国璋等利用三次B－样条分形插值曲线，给出了求S（x s，ys）的代数解法［7］。然而此法在实用上很不方便，下面基于Mazel和Hayes的几何法，提出一种在实用上非常方便的求取d i的几何方法。它无需计算插值曲线上的最大值点S（x s，y s），也不用借助其它的解析工具，仅仅利用离散数据自身的信息，就可确定d i的值。

设有时间序列｛Y t，t＝0，1，…，M｝，按下列方式将其等分成长度为n＋1的N个连续的子序列I i，i＝1，2，…，N。记子序列Ii中的每个元素为Y k，i（0≤k≤n），且有Y n，i＝Y0，i＋1（i＝1，2，…，N－1）（亦即每个子序列的最后一个元素的值等于相邻的下一个子序列的第一个元素的值），则有M＝n·N。取所有子序列Ii，i＝1，2，…，N的第一个元素的集｛Y0，1，Y0，2，…，Y0，N｝与第N个子序列I N的最后一个元素Y n，N（或者所有子序列Ii，i＝1，2，…，N的最后一个元素｛Y n，1，Y n，2，…，Y n，N｝的集与第一个子序列I1的第一个元素Y0，1）所构成的元素集｛Y0，1，Y0，2，…，Y0，N，Y n，N｝作 为 时 间 序 列 ｛Y t，t＝ 0，1，2，…，M｝的抽样数据，共有N＋1个数据。为方便起见，将｛Y0，1，Y0，2，…，Y0，N，Y n，N｝简记为｛y0，y1，…，y N｝与其相对应的时间值设为｛x0，x1，…，x N｝。于是（x0，y0），（x1，y1），…，（x N，y N）构成时间序列曲线上的一组插值点集。

设子序列Ii的每个元素Y k，i所对应的时间值为X k，i，0≤k≤n，则相应于Ii的两个端点数据为

这样对于给定的时间序列｛Y t，t＝0，1，…，M｝，通过适当的抽样，选定了N＋1个插值点（x0，y0），（x1，y1），…，（x N，y N）。再由上面提出的方法就可确定N个纵向尺度因子d i，i＝1，2，…，N的值。

在利用分形插值对股指时间序列进行拟合时，假设股指数据有n×N＋1个，按照上面的方法，抽样选取的股指序列为｛y0，y1，…，y N｝，相应的时间序列为 ｛x0，x1，…，x N｝，这 样 得 到 插 值 点 集 ｛（x i，y i）：i＝0，1，2，…，N｝。由式（4）确定d i，i＝1，2，…，N，再根据式（1）、（3）就确定了一个能生成仿射分形 插 值 函 数 的 迭 代 函 数 系 ｛R2；w i，i＝ 1，2，…，N｝。

利用已知的股价来预测未来的股价走势是令人感兴趣的问题，然而这也是极其困难的问题。因为股价的走势受到多种因素的影响，目前并无好的方法来预测股价的走势。笔者尝试利用分形插值的外推功能来预测股价在未来时间［x N，x N＋1］上的变化趋势。将定义在［x0，x N］上的分形插值函数f（x）的定义域推广到［x0，x N＋1］（x N＋1＞x N）上，以预测f（x）在［x N，x N＋1］上的值。设y N＋1是对应于时间x N＋1时的股价，它的值可根据股票价格的拟周期性以及统计自相似性给出一个经验估计。为此在［x N，x N＋1］×R上 定 义 一 个 仿 射 变 换w N＋1（x，y）＝（L N＋1（x），F N＋1（x，y）），使得：

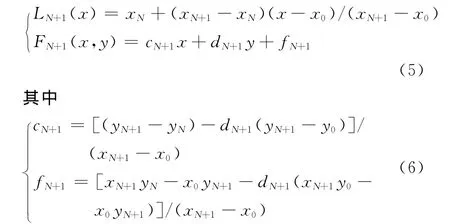
这里d N＋1的值可根据金融时间序列的长期相关性，取为：

将w N＋1与之前的w i，i＝1，2，…，N一起构成一个新的迭代函数系｛R2；w i，i＝1，2，…，N＋1｝，便可预测时间段［x N，x N＋1］上的股价值。

三、实证分析

选取上海股票市场上证综合指数每日的收盘指数作为研究对象，对股指时间序列从2006年5月11日至2010年9月15日的1 061个交易日股指数据进行分析和预测，图1为原始数据图。先对2006年5月11日至2010年6月30日的1 008个交易数据进行分形插值拟合，把这些数据按时间进行等距分割，使得x i＝53i＋1，i＝0，1，…，19，取（x i，y i），i＝0，1，…，19为插值点集，即为构造仿射分形插值函数所需的插值点，选取的数据如表1所示。根据式（4）求得纵向尺度因子d i分别为：d1＝0.034 5，d2＝－0.044 1，d3＝ －0.073 6，d4＝ 0.076 1，d5＝－0.108 5，d6＝－0.243 4，d7＝0.232 5，d8＝0.248 9，d9＝0.127 5，d10＝0.150 5，d11＝－0.086 8，d12＝－0.116 1，d13＝0.089 5，d14＝0.050 3，d15＝0.087 3，d16＝ －0.155 9，d17＝0.062 7，d18＝－0.076 8，d19＝－0.067 9。再由式（3）确定仿射迭代函数系的其它系数。这样就唯一地确定了一个含有19个仿射变换的迭代函数系。利用确定性迭代算法，经过3次迭代得到如图2所示的分形插值拟合曲线。

比较图1和图2发现，虽然在前1 008个数据的原始图与分形插值拟合图之间存在着一定的误差，但是拟合图与原始数据图的变化趋势是一致的。而且如果适当增加插值点的个数并增加迭代次数，将会更好地模拟原始数据图，这也说明利用分形插值法来模拟股指的波动状态是可行的。

表1 抽样数据表

图1 上证指数的原始数据图

图2 上证指数的分形插值拟合图

下面利用分形插值外推法对上证综指的变化趋势进行预测。选取上证综指从2010年7月1日至2010年9月15日的53个交易日的收盘指数作为预测对象。设x20＝53×20＋1。根据股票价格的拟周期性以及统计自相似性，经验估计y20的值为2 600。由式（7）得到d20＝0.009 8，再由式（5）、（6），得到w20＝ （0.05x＋1 007.95，0.18x＋0.009 8y＋2 382.816）。于是确定了一个新的迭代函数系｛R2；w i，i＝1，2，…，20｝，经过三次迭代，得到了股指在2010年7月1日至2010年9月15日这一段时间内的预测图，结果如图3所示。从图3可以发现，利用分形插值得到的预测结果与原始数据的基本趋势是一致的，由此表明利用分形插值法来对股票指数进行预测是可取的。

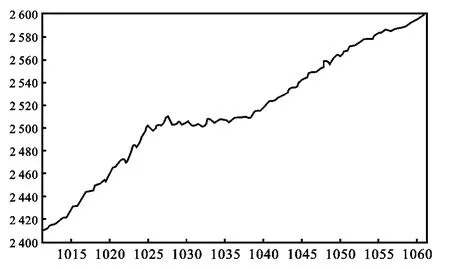
图3 上证指数的分形插值预测图

为了刻画上证综指的结构特征，使用R／S分析法和Hurst指数对其进行特征分析。R／S分析法即重标极差分析法（Rescaled Range Analysis），是Hurst在大量实证研究的基础上提出的一种非参数统计方法，该方法主要通过Hurst指数来刻画时间序列的结构特征。R／S分析法的表达式为：

其中（R／S）n表示时间序列｛Y t，t＝1，2，…，n｝的重标极差，C为常数，H为Hurst指数。对式（8）两边取对数得：

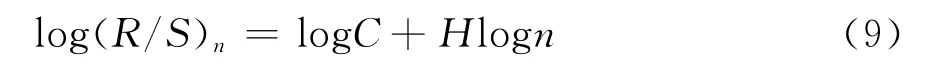
在重对数坐标系logn－log（R／S）n中，运用回归分析法求出直线的斜率H即得Hurst指数。

在金融市场分析中，由于原始数据往往受到自相关性的影响，需要对原始数据消除或降低线性依赖性，通常以对数收益率作为研究对象。若以｛Y t｝表示原始数据构成的时间序列，设对数收益率序列为｛St｝，则：

下面首先对上证综指从2006年5月11日至2010年6月30日的1 008个股指序列计算其对数收益率，得到对数收益率序列｛St｝，其长度为1 007。其次对｛St｝作R／S分析，此时总数据个数T＝1 007，令T＝M×n，这样就把｛St｝分成了每组有n个数据的M组子样本。我们从第一个n＝10开始，对每一组的子样本计算重标极差R和标准差S，从而得到M个R／S，进而可得到这M个R／S的平均值，记为（R／S）n。重复上述过程，直到n＝ ［T／2］＝503。最后由式（9）可估计出Hurst指数H。绘制log（R／S）n关于logn的重对数图，如图4所示，其中直线的斜率就是Hurst指数的估计值H＝0.669。由于0.5＜H＜1，表明上证综指具有状态持续性。由时间序列的分形维数D和Hurst指数H的关系可知，这段时间内股指对数收益率序列的分形维数D＝1.331，表明序列具有分形统计结构特征。

图4 上证指数日收益率的R／S分析图

四、结束语

本文基于Mazel和Hayes的几何法，提出了一种新的计算迭代函数系纵向尺度因子的方法，据此建立了能够用于分析和预测股指波动的仿射分形插值模型。以上海股票市场上证综合指数的每日收盘指数为研究对象，选取2006年5月11日至2010年9月15日期间的1 061个交易日的收盘指数进行分析和预测。结果表明：基于分形插值理论对股票指数的模拟和预测是可行的，而且模拟和预测结果与实际情况较为吻合。文章同时运用R／S分析法和Hurst指数，分析了上证综合指数的结构特征，说明上证综指具有状态持续性和分形统计结构特征。

［1］ Peters E.Fractal Market Analysis：Applying Chaos Theory to Investment and Economics［M］.New York：John Wiley＆Son Inc.，1994.

［2］ 黄诒蓉.中国股市分形结构：理论与实证［M］.广州：中山大学出版社，2006.

［3］ 周洪涛，王宗军.上海股市非线性特征：一个基于R／S方法的实证分析［J］.管理学报，2005，2（5）.

［4］ 申富饶，王嘉松.股票价格的一种线性分形预测方法［J］.南京大学学报：自然科学版，1999，35（4）.

［5］ Mazel D S，Hayes M H.Using Iterated Function Systems to Model Discrete Sequences［J］.IEEE Transactions on Signal Processing，1992，40（7）.

［6］ Barnsley M F.Fractal Functions and Interpolation［J］.Constr.Approx.，1986，2（4）.

［7］ 李国璋，黄建波，黄海英.基于B－样条分形插值的垂直尺度因子的计算方法［J］.军械工程学院学报，2006，18（2）.

27

Fractal Interpolation Models and R／S Analysis on Stock Index Time Series

WANG Hong－yong，ZHANG Qing－ge

（School of Applied Mathematics，Nanjing University of Finance ＆Economics，Nanjing 210046，China）

The law of change and the structure feature of stock index time series are investigated by using fractal interpolation models and R／S analysis in this paper.We study the law of change of the Shanghai Composite Index during a certain time by establishing fractal interpolation models，and predict the tendency of change of the index in the short term.Using R／S analysis and Hurst exponent，we analyze the structure feature of the Shanghai Composite Index，and point out that the market has the persistence of state and the statistical properties of fractal distribution.

fractal interpolation；stock index time series；R／S analysis

（责任编辑：崔国平）

F224.9∶F830.9

A

1007－3116（2011）08－0023－05

2011－05－03

国家自然科学基金项目《Sobolev空间上Framelets理论及相关问题研究》（11071152）

王宏勇，男，江苏扬州人，理学博士，教授，研究方向：分形理论及应用；

张青格，女，河北邢台人，硕士生，研究方向：分形与数理金融。

【统计理论与方法】