基于立方体元的Shear－warp体绘制加速算法

周大鑫，周茂林，邹 文，鲁 才

(1.电子科技大学 计算机科学与工程学院，四川成都 611731;2.川庆钻探工程有限公司 地球物理勘探公司，四川成都 610213;3.电子科技大学宽带光纤传感与通信教育部重点实验室，成都 611731)

基于立方体元的Shear－warp体绘制加速算法

周大鑫1，周茂林2，邹 文2，鲁 才3

(1.电子科技大学 计算机科学与工程学院，四川成都 611731;2.川庆钻探工程有限公司 地球物理勘探公司，四川成都 610213;3.电子科技大学宽带光纤传感与通信教育部重点实验室，成都 611731)

大规模三维地震数据的直接体绘制，是一个计算和数据双重密集型问题。为了提高三维图像的重建效率，提出了一种基于立方体元的Shear－warp地震数据体绘制算法。该算法通过构建立方体元在相邻的体素点之间建立联系;然后根据地震数据的特征对体元进行分类，在绘制过程中通过二叉树索引，快速定位分类结果。通过索引结果，避免了对等值体元的插值计算和跳过透明体元，提高了绘制速度。经实验结果表明，Shear-warp算法得到了有效加速。

可视化;体绘制;地震数据;二叉树;Shear-warp

0 前言

直接体绘制是近年来迅速发展起来的，对三维数据场的一种体可视化绘制方法。该方法可以非常清晰地反应出三维数据场的细节，并且能够将面绘制不能显示的三维数据内部构造显示出来。由于直接体绘制能够对来自于地质勘探、核磁共振、计算机断层扫描、计算机流体力学等的三维体数据进行有效的绘制，所以体绘制技术在石油勘探、生物医学工程、地质科学、气象、有限元分析后处理、化学等领域得到了广泛地应用和重视［1］。近年来，体绘制技术又被应用于考古和文物保护、宇航、地震预测、自然现象仿真等领域。

三维地震是目前石油勘探的主要手段，由于三维地震数据的数据量很大(例如一个普通三维工区有1024×1024个道，每道有5000个点，每个点为一个浮点数存储，其大小为20G，相对现有的普通微机内存是很难将其全部载入)，因此其体绘制是一个计算和数据双重密集型问题。如何在不损失最终绘制结果质量的前提下，通过提高体绘制的成像速度来达到交互式体绘制，对于推动直接体绘制技术在石油勘探领域进一步应用具有重要的实际意义，并已成为国内、外石油工业界和学术界共同关心的前沿问题。

传统的体绘制方法有光线投影算法(Ray-Casting)［2］，足迹表法 (Splatting)［3］和错切变换(Shear-warp)［4］等。近年来，国内、外学者也提出了很多加速体绘制的方法，如包围盒空间八叉树(Octree)［5］等数据结构和提前不透明度截至［6］等策略来加速体绘制算法，也有通过基于三维纹理硬件［7］、基于可编程图形处理器(GPU)［8］等硬件方式加速体绘制的方法。但由于计算量大，计算复杂度高，很难达到交互式体绘制的要求。基于硬件的体绘制算法，由于硬件价格昂贵和纹理显存有限等原因也难以普及。相对而言，目前Shear-warp算法的速度最快［9］。

Shear-warp算法通过矩阵变换的方式，将绘制过程分解成三维数据场shear和二维图像的warp两个过程，以达到将三维数据场的重采样和插值过程转变为对二维平面的重采样和插值过程，从而简化了计算复杂度和计算量。

在Shear-warp算法实现过程中，可以采用多种加速方法。如文献［5］中的八叉树编码体数据，实现对体数据的快速编码，还有游程编码(RLE)［10］数据结构加速的方式，都能跳过大规模“透明”的无效体素，从而达到加速算法的目的。但是，当体数据的透明度发生变化之后，八叉树编码和RLE都要重新对体数据进行编码，需要额外的预处理时间，这样对体绘制的交互性造成了影响。而且这两种方法都只考虑了体数据中的透明无效体素，没有考虑到在体数据中存在的相邻数据值相同的情况。同时RLE方法需要在每个主方向存储一套切片，这对于大规模的三维地震数据而言，增大了内存消耗，从而增加了数据读取时间。

针对上述问题，作者在本文中提出了基于立方体元的Shear-warp地震数据体绘制算法。该算法通过立方体元的方式，使相邻的体素点之间建立联系，从而在计算的过程中，能够有效地利用地震数据空间关系对体绘制进行加速。体元作为存储和绘制的基本单位，当绘制的主方向发生变化时，通过改变Shear-warp算法扫描线的方向，对一份数据进行操作，相对RLE的编码方式节省了存储空间。同时，可根据地震数据的特点对立方体元进行分类，然后采用二叉树对分类进行快速索引。通过索引结果，在绘制过程中不仅跳过了“透明”的无效体素，而且还避免了对相同地质体中重采样点的插值计算，从而提高了Shear-warp算法的绘制速度。

1 利用立方体元实现Shear-warp加速算法

Shear-warp地震数据体会制算法的整个流程，可以划分为两个阶段:

(1)数据预处理阶段。

与大型出版企业相比，中小出版企业在资源垄断、出版许可、网点布局、文化沉淀、社会责任等方面差距较大。因此，中小出版企业转型升级不能效仿大企业的“高、大、上、全”。

(2)绘制阶段。

如图1所示，预处理阶段包括立方体元数据结构的压缩和存储，二叉树索引结构的建立。绘制阶段包括透明立方体元的跳跃，对不同体元的插值处理方式，以及颜色和不透明度的映射。

1.1 数据预处理

1.1.1 地震数据压缩和道的立方体元转换

对于三维数据场D的数据分布，通常可以通过某个函数f3D(x)来定义，为了达到压缩三维数据场的目的，我们通过门槛分类法把数据分为256个区间。如n+1个门槛值0=S0＜S1＜S2、…、＜Sn－1＜Sn=256，把数据场分为n部份，对数据场 D=D0∪ D1∪ 、…、∪ Dn－1。其中Di={x|Si＜=f3D(x)＜Si+1}，i=0、1…、n－1。函数f3D(x)就是将每个采样点x映射到特定的区间［Si，Si+1)。映射函数f3D(x)如下:

f3D(x)=

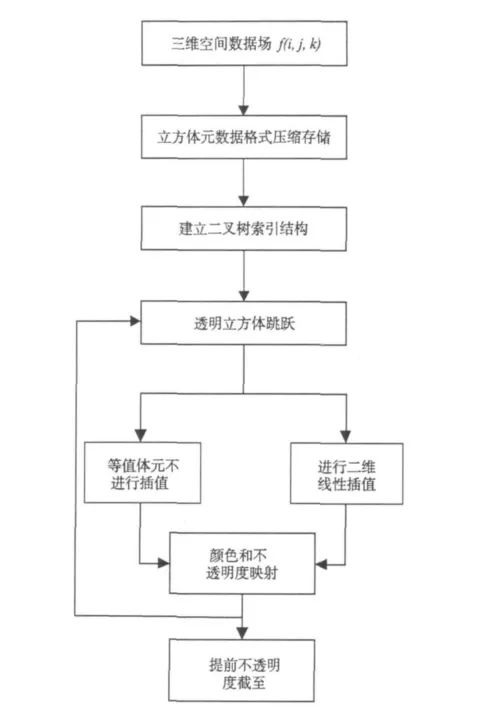
图1 绘制流程Fig． 1 Rendering process

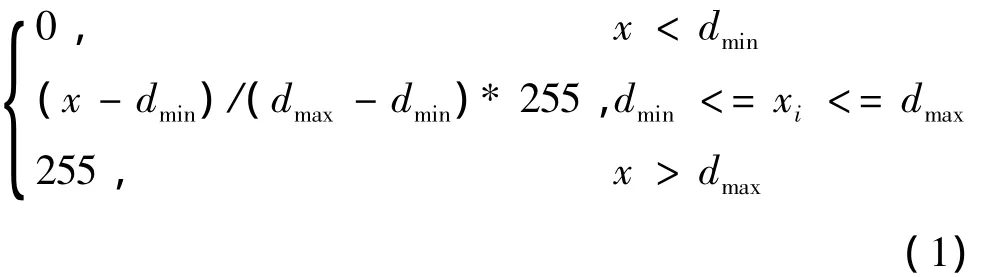
式中 dmin、dmax为原始数据的最小值与最大值;x为原始数据;f3D(x)为压缩后的数据值。

三维地震数据的数据值分别代表地质体的不同属性，如沙层、岩层等之间不同的密度值。而三维地震数据中有大量相邻的相同地质体存在(如下页图2所示)，合理利用地震数据中相同地质体的空间关系，可以对算法进行有效加速。原始的三维地震数据通常是以点为单位，然后按道的方式进行存储(见下页图3(a))，由于点的结构难以反映三维地震数据的空间关系。因此作者采用立方体元，为基本单位的结构进行存储，将以点为单位的地震道转换为以体元为单位的数据道(如图3所示)。使每个体数据点和周围七个点通过立方体的方式发生联系，同时按体元的方式对体数据进行存储和处理。

图2 三维地震数据剖面Fig． 2 3D seismic data profile

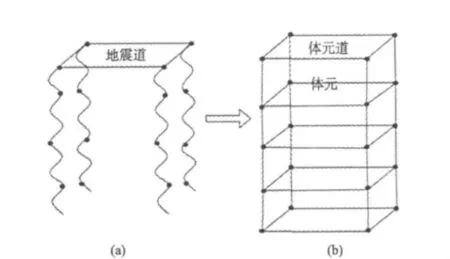
图3 地震道到体元道的转换Fig． 3 Transition of seismic trace to volume element

因为相同的地质体具有相同的体数据值，而相同的体数据在通过传递函数映射之后，必然得到相同的颜色值和透明度。Shear-warp算法对重采样点的值进行计算的时候，采用的是线性插值算法，若C为AB连线上的一点，公式(2)为一次线性插值算法，其中 va和 vb表示点 a和 b的值，α=CB/AB。若 va=vb，那么 vc=va=vb。

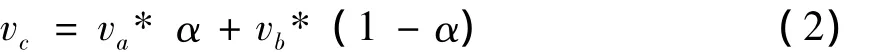
因此如果一个立方体元的八个顶点值相同或值相近，对在这个立方体元六个面上的重采样点的值，就与顶点的值相同。在此我们认为，一个立方体元的八个顶点的差值如果小于定义的闸值，则这个立方体元为一个等值体元。因此，通过对等值体元进行提取分类和有效索引，可以减少插值次数和跳过透明体元。

如图4所示，作者对地震数据体元道采用了二叉树索引结构。二叉树的节点中包括了指向数据起始体元的指针p和等值体元个数size，以及标识体元是否透明的flag。若一个立方体元道内的所有体元都是等值的，那么二叉树只有一个根节点。否则将体元道进行上下等分，使二叉树的子节点只有父节点的n/2个体元。通过递归分类之后，将体元道所有的体元都进行分类。如果颜色和不透明度发生改变，只需要改变传递函数的映射规则，将二叉树节点中的透明标志改为不透明，然后在第一次绘制的过程中，改变透明体元的二叉树索引节点中的透明标志，不需要重新构建二叉树索引结构(八叉树编码和游程编码都要重新构建索引结构)。二叉树索引结构中的非叶子节点的size值，代表当前节点子孙节点的体元个数，叶子节点的size值，代表当前体元(包括当前体元)之后等值体元的个数。在绘制过程中，可以通过二分查找在二叉树索引中快速查找到对应体元的索引节点。

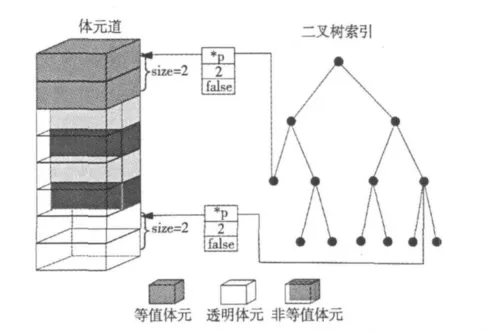
图4 二叉树索引结构建立过程Fig． 4 Process of creating binary tree index

1.2 基于立方体元的Shear-warp体绘制

1.2.1 基于存储方向的体扫描线

传统的Shear-warp算法采用游程编码(RLE)的数据结构加速数据场的遍历。RLE需要建立三份垂直于主观察方向的编码数据，每组编码数据重采样时，都以扫描线为遍历的步长单位。对于本来就规模庞大的三维地震数据，三份编码数据增大内存消耗的同时也提高了数据访问的时间。

作者采用基于体元道存储顺序的体元扫描线方式(如下页图5所示)。该方式在任意的主观察方向上，都采用和体元的存储方向一致的体元扫描方式。按照存储方向访问数据，提高了高速缓冲存储器的命中率，只存储一份数据，也减少了内存的消耗。在从前向后融合的过程中，把每个体元道中对采样点的融合的中间结果记录在一个二维数组中，该二维数组记录了Shear－warp错切空间中二维平面像素融合的值。在对下一个体元道进行计算的时候，再读取该二维数组的值带入融合计算。

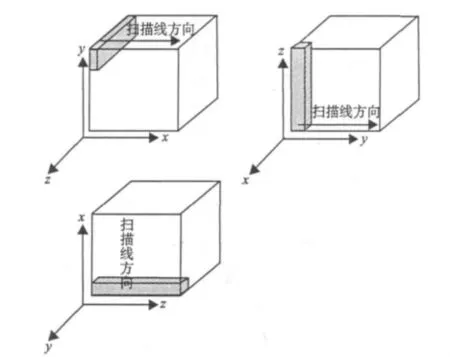
图5 基于存储方向的体扫描线Fig． 5 The volume scanning line based on storage direction

1.2.2 绘制流程

体绘制的绘制流程就是对重采样点进行融合，形成最终图片的过程，而减少对重采样点值的计算量是对体绘制加速的主要环节。作者提出的算法通过对二叉树索引的快速查询，避免或减少了对重采样点的计算。每个重采样点的绘制流程可以分以下步骤:

(1)遍历每一个重采样点(x，y，z)，计算其所在的体元编号，并在二叉树索引中进行二分查找对应体元索引节点N。

(2)判断节点N的透明标识flag，如果flag为真，则表示该体元全透明，返回步骤(1)处理下一个重采样点;否则，则进入步骤(3)。

(3)判断该体元是否为等值体体元，如果为等值体，则将该重采样点的值用体元值替换，并通过采用Shear-warp算法采样步长单位等距的特点，快速处理下一个重采样点而无需再次查找该采样点的体元索引，转到步骤(1)处理下一个采样点;如果该节点是非等值体，则进入步骤(4)。

(4)对于非等值体节点采用二维线性插值获得采样点的值。

在绘制过程中遇到等值体时的时候，可以通过Shear－warp算法采样步长单位等距的特点，快速处理下一个重采样点而无需再次查找该采样点的体元索引。同时，当Shear-warp错切空间中像素融合结果值的透明度大于设定闸值的时候，提前终止该像素点从前向后的融合过程。

2 实验结果与分析

我们使用C++和OpenGL实现了基于游程编码(RLE)的Shear－warp算法和作者在文中所描述的算法，所用的机器配置为IntelDual-core2.5 GHz双核，2G内存，ATIHD3600显卡，256MB显存，windows7系统。实验数据为200×400×1100的地质断层数据，实验结果如下页表1。图像如图5所示。表1中对等值体元定义的闸值大小分别对应图5中的绘制效果。

图6 不同闸值在相同颜色和透明度下的绘制结果Fig． 6 The drawing result of different brake value in thesame color and transparency

从表1的结果可以看出，新算法的加速比受等值体元进行定义的闸值大小影响。若闸值增大，等值体元增多，插值计算量减小，算法速度提高。但是通过图6(见上页)的绘制结果可以看出，闸值越大，被近似当做透明和等值的重采样点增多，使重采样点误差增大，从而降低了体绘制图像的质量。因此如何定义闸值的大小，要通过实际应用中的需求调整，才能达到不影响质量的情况下最大限度地提高体绘制速度。

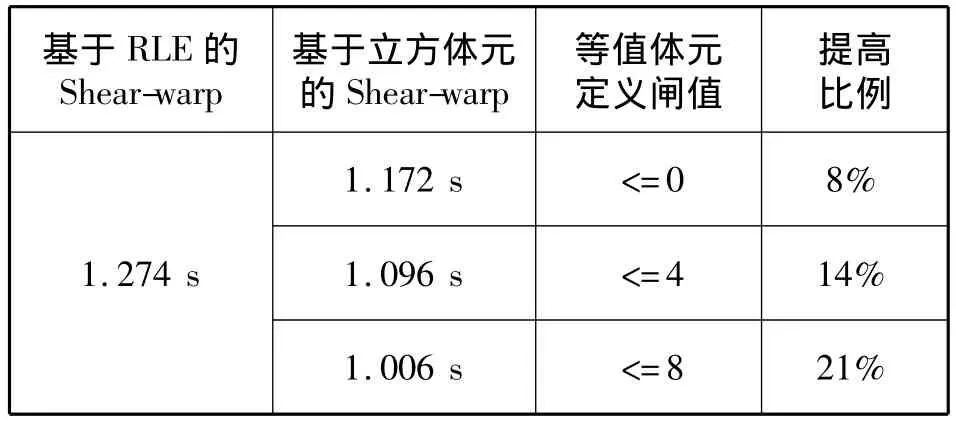
表1 绘制时间比较Tab． 1 Time-consumes

3 结束语

作者在本文中根据三维地震数据自身的特点，用立方体的方式模拟了地震数据的空间关系。通过对相同地质体的分类，该算法在绘制时只对周围点的值都不相同的重采样点进行插值计算，忽略了透明体元和相同地质体上重采样点的插值计算。当地震数据中有大规模的相同地质体时，本文中算法的加速效果将更加明显。

通过对地震数据的绘制结果证明，本算法相对游程编码的Shear-warp算法绘制速度有了显著的提高。

［1］ 唐泽圣.三维数据场可视化［M］.北京:清华大学出版社，1999.

［2］ LEVOYM.Displayofsurfacesfromvolumedata［J］.IEEEComputerGraphics＆Applications，1988，8(3):29.

［3］ WESTOVERL.Footprintevaluationforvolumerendering［J］.ComputerGraphics，1990，24(4):367.

［4］ LACROUTEP，LEVOYM.FastVolumeRenderingUsing Shear－WarpFactorizationoftheViewingTransformation［J］.ComputerGraphicsproceedin － gs.July.1994:451.

［5］ 宋涛，欧宗瑛，王瑜，等.八叉树编码体数据的快速体绘制算法［J］.计算机辅助设计与图形学学报，2005，9:1991.

［6］ MATSUIM，INOF，HAGIHARAK.Parallelvolumerenderingwithearlyrayterminationforvisualizinglargescaledatasets［A］.ISPA2004［C］.2004.

［7］ 许庆功，刘庆伟，张永胜.基于硬件加速的纹理映射体绘制［J］.计算机工程与应用，2009(26):190.

［8］ 苏超轼，赵明昌，张向文.GPU加速的八叉树体绘制算法［J］.计算机应用，2008，9:1232.

［9］ SORENG，STEFANB，ARMINK，etal.MemoryefficientaccelerationstructuresandtechniquesforCPU-basedvolumeraycastingoflargedata［A］.IEEESymposiumonVolumeVisualizationandGraphics2004［C］.Austin，Texas，USA:2004.

［10］ LACROUTEP.FastVolumeRenderingUsingaShear-WarpFactorizationoftheViewingTransformation［D］.(Ph.D.dissertation).America.StanfordUniversity，1995.

TP391.41

A

1001—1749(2011)05—0563—05

国家自然科学基金重点项目资助(40839905);教育部“新世纪优秀人才支持计划”资助(NCET-07-0148)

2011－07－04 改回日期:2011－07－14

周大鑫(1986－)，男，四川木里人，硕士，研究方向:计算机图形。