GPU 提速叠前时间体偏移技术

张慧宇，刘路佳，张 兵，刘伟峰，周李军

(1.中国石化石油物探技术研究院，江苏南京 210014;2.中国石化石油勘探开发研究院 信息技术研究所，北京 100083;3.中国石油化工集团公司 多波地震技术重点实验室，北京 100083)

GPU 提速叠前时间体偏移技术

张慧宇1，刘路佳1，张 兵1，刘伟峰2，3，周李军1

(1.中国石化石油物探技术研究院，江苏南京 210014;2.中国石化石油勘探开发研究院 信息技术研究所，北京 100083;3.中国石油化工集团公司 多波地震技术重点实验室，北京 100083)

为了进一步提高叠前时间体偏移的计算效率，实现了在GPUCPU协同并行计算模式下Kirchhoff叠前时间体偏移技术，并进行优化。经在NvidaTeslaC1060GPU上的测试表明，GPU(GraphicProcessingUnit)的处理速度是CPU(单核)的四十倍左右。同时表明，CUDA(ComputeUnifiedDeviceArchitectare)编程为CPU向GPU的转化提供了一个较为方便的语言环境。

CUDA编程;GPU计算;Kirchhoff叠前时间体偏移;并行计算

0 前言

随着勘探技术的发展，地震数据规模越来越大，对处理周期的要求却越来越短，意味着地震数据处理对计算设备的要求不断提升。近两年来，由于GPU拥有强大的并行计算能力，使得 GPU计算在地球物理领域的研究受到广泛关注［1］。美国休斯顿的Headwave公司是一家专门从事地学数据分析的公司，开发了新一代计算平台，支持叠前地震数据的分析与解释。在平台开发中，充分利用图形卡的并行计算潜力，以支撑实时工作流程、实时可视化和实时计算。Headwave公司采用了NVIDIA的GPU计算产品，使用CUDA软件环境。通过GPU计算技术的采用，大大加快了地球物理数据分析的速度。Peakstream公司采用二种克希霍夫偏移计算算法的变种，对GPU加速性能进行了试验，取得了最高达二十七倍的加速结果。

地震数据处理主要包括三大模块:反褶积、叠加、偏移。其中，偏移是整个处理过程中最复杂最耗时的环节。偏移的方法有很多种，叠前偏移和叠后偏移、时间偏移和深度偏移、二维偏移和三维偏移等。三维Kirchhoff积分法叠前时间偏移是一种常用的偏移方法，具有成像精度高，偏移速度较快的特点，适合于横向速度变换不太大地区的地震数据处理。若将该方法用GPU进行提速，会进一步缩短处理周期，提高计算效率，加强实用化程度。

1 GPU 计算与 CUDA 编程［2～5］

GPU是图形处理单元(GraphicProcessingU-nit)的简称，是目前通用计算机系统中专门从事图形计算的单元，其应用极为广泛。与常规CPU不同的是，GPU中大部份晶体管被用来进行数据处理(见下页图1)，只有少量被用作数据缓存和指令流控制。因此，GPU特别适合运行单程序多数据流的数据并行处理任务，即主要支持SPMD并行计算模式。目前，GPU的计算性能已达1TFLOPS。

CUDA(ComputeUnifiedDeviceArchitecture，计算统一设备架构)是NVIDIA公司2007年推出的GPU通用计算产品，是一种将GPU作为数据并行计算设备的软、硬件体系。CUDA采用了比较容易掌握的类C语言进行开发，开发人员不必重新学习语法。CUDA将用于GPU上计算的并行代码用NVCC编译器编译，用于CPU上进行计算的串行代码用标准的C编译器进行编译。此外，CUDA除了提供C语言编程接口外，还提供Fortran语言编程接口。这里，我们利用C语言调用CUDA子程序，来实现基于GPU的叠前时间体偏移算法。所用的GPU设备是NVIDIA公司生产的TeslaS1070，包含四块TeslaC1060卡，每块有240个核，主频为1.30GHz，浮点运点能力达到1TFLOPS。

图1 CPU与GPU晶体管的使用Fig． 1 GPU use more transistors in computing

2 Kirchhoff积分法叠前时间体偏移［6］

一般的Kirchhoff积分法叠前时间偏移是按输出道的观点，把一个输入的地震道振幅按Kirchhoff积分偏移公式，发散到不同时刻的等时面上，这种方案适合小规模数据体计算。但是，在进行大规模数据的积分法叠前成像处理时，该方案的缺陷就非常明显:由于偏移孔径很大，导致输入数据的重复次数很多，大大增加了I/O量。为了克服这一缺点，作者在本文采用适于大规模数据的三维Kirchhoff积分法叠前时间体偏移方法。

与一般的Kirchhoff积分法叠前时间偏移不同，该方法是按共偏移距数据体进行偏移成像，其处理流程如图2所示。

(1)数据按偏移距进行排序。

(2)对每个共偏移距数据体进行并行体偏移计算;按共偏移距数据体中的Inline线分配作业，每条线一个进程;每个进程的成像输出空间大小，等于叠加后的全局成像数据体，放在局部盘上。

(3)一个共偏移距数据体偏移完后，规约收集每个处理器对应的局部盘上的成像结果;把规约叠加后的结果移到全局盘上;清除局部盘上的空间，为下一个共偏移距数据的偏移做准备。

(4)所有偏移距的数据偏移完，全局盘上就有了所有偏移距数据对应的成像结果;重排序可以得到每点的成像道集;成像道集修饰叠加，可以得到最后的叠前偏移成像结果。

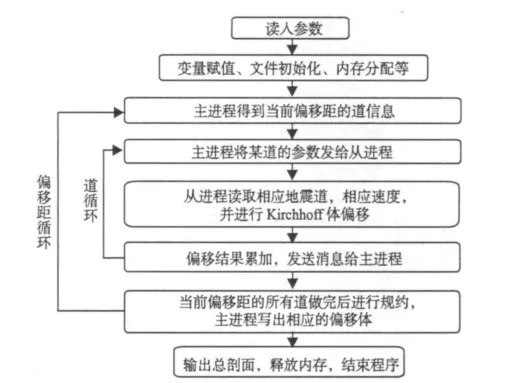
图2 叠前时间体偏移流程图Fig． 2 Technological process of seismic prestacktime migration

3 基于GPU的算法实现

GPU的优势在于天生的并行计算体系结构，但在逻辑判断、非线性寻址等方面，却远不如CPU。因此，使用GPU处理数据并行任务，而由CPU进行复杂逻辑和事务处理等串行计算，就可以最大限度地利用计算机的处理能力。作者的研究，正是在GPUCPU协同并行模式下实现的。

(1)首先基于上述流程，对算法进行并行分析。可以看出，该方案主要有两层循环，外层的偏移距循环和内层的道循环。由于GPU的显存有限，只有4G，所以采用将道循环在GPU上运行的方案。

图3 算法各部份计算时间统计Fig． 3 Time statistics of algorithm of each part

(2)在初步确定并行方案后，对程序中的各个子函数进行时间测量，找出其中的“热点”函数，着重进行GPU改造。图3为算法各部份计算占用时间的统计，由图3可见，偏移内核函数(pstmkir3dnew)占用了绝大部份的计算时间，而FFT计算时间及GPUCPU数据传输时间分别各占2%，其它函数计算时间几乎可以忽略不计，所以我们主要关注偏移内核函数的优化。

基于GPU的内核函数优化，最重要的是如何分配线程层次。对GPU而言，有三级并行层次，即:线程、线程块，线程网格。作者在本文中方法基于成像体空间分配线程层次，每个线程计算三维成像体横截面的一个成像点，将整个成像横截面规则地分成多个线程块，再由整个线程块结构组成一个线程网格，结构见图4。

图4 线程分配策略Fig． 4 Thread allocation strategies

通过以上步骤，基本上实现了算法的GPU改造。为了进一步提高计算效率，还需要做一些算法优化。

4 基于GPU的算法优化

(1)减少数据I/O时间。我们知道，在传统的集群计算中如何降低数据I/O消耗非常重要。在基于GPU的计算中，由于GPU的计算速度非常快，所以数据I/O问题更加显著。

前面已经提到，CUDA具有三层并行层次，相对于这三个层次，CUDA也提供了三层存储器结构:①线程本身的寄存器和局部存储器;②线程块的共享存储器;③线程网格的全局存储器。此外，还有两种只读存储器:常数存储器和纹理存储器［2］。相对于GPU的高速计算能力，GPU对片外存储器的访存具有较高的访存延迟。为解决这一难题，就要充分发挥各种存储器的作用。例如:将一些全局常量存入常量存储器，以便利用GPU上的常量cache减低对片外显存的访问量。

(2)利用CUDA提供的一些快速计算函数。在不影响精度的前提下，可以使用CUDA所提供的内建函数，来提高计算效率，如:__sinf(x)，__fdividef(x)，__expf(x)等。

通过上述算法优化，可使基于GPU的叠前时间体偏移计算效率速度提升近四十倍。

5 数据测试

为了验证算法的正确性及运算效率，作者采用某三维数据进行了数据测试。该工区覆盖面积为54.17km2，总道数达594 ×104，记录时间6s，采样2ms，数据总体大小为73GB。该工区的特点是有负向背斜构造及大倾角构造，偏移参数为:成像网格为25m×25m，最大偏移孔径为8000m，最大成像角度In_line和Cross_line方向分别为60°和30°，测试环境如表1所示。

表1 测试环境Tab． 1 Test environment

偏移剖面局部图如下页图5所示。在图5展示的两个剖面，从视觉上看不出差别。为了比较CPU计算结果和GPU计算结果的精确误差，我们采用下述的均方误差公式，对数据进行误差分析与统计，如下页图6所示，纵轴为百分比，横轴为相对误差大小(千分之)。

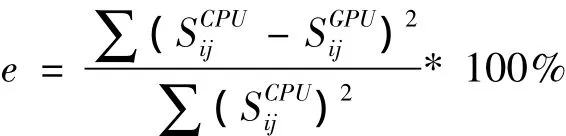
通过分析计算，偏移剖面的均方误差大小为:0.002%，其中相对误差小于0.1%所占的比重为85.48% ，可以说明基于GPU的三维叠前时间体偏移算法是正确的。计算时间如下页表2所示。

由表2可以看出，GPU单卡相对于CPU单核的加速比约为四十倍。

6 结论

作者在本文中实现了基于GPU的三维叠前时间体偏移技术，经在NvidaTeslaC1060GPU上的测试表明，GPU的处理速度是CPU(单核)的四十倍左右。该方法为将来做大规模数据处理，提供了高效的技术平台。同时表明，CUDA编程为CPU向GPU的转化，提供了一个较为方便的语言环境。经过此次技术积累，要加快偏移新方法以及其它处理技术向GPU平台的移植进度，以适应当前地球物理技术的发展。

图5 某三维数据测试结果局部剖面Fig． 5 Image after pstm on CPU and GPU

图6 误差统计图Fig． 6 Error statistical figure

表2 某三维数据测试时间对比Tab． 2 Time contrast diagram of test 3D data

［1］ 赵改善.地球物理高性能计算的新选择:GPU计算技术［J］.勘探地球物理进展，2007，30(5):399.

［2］ 张舒，褚艳利，赵开勇，等.GPU高性能运算之CUDA［M］.北京:中国水利水电出版社，2009.

［3］ 张兵，赵改善，黄俊，等.地震叠前深度偏移在CUDA平台上的实现［J］.勘探地球物理进展，2008，31，(6):427.

［4］ 王华忠，蔡杰雄，孔祥宁，等.适于大规模数据的三维Kirchhoff积分法体偏移实现方案［J］.地球物理学报，2010，53(7):1699.

［5］ 孔祥宁，赵改善，王华忠，程玖兵.叠前偏移计算中多文件并行 I/O技术［J］.物探化探计算技术，2005，27(2):97.

［6］ 刘国峰，刘洪，王秀闽，等.Kirchhoff积分叠前时间偏移的两种走时计算及并行算法［J］.地球物理学进展，2009，24(1):131.

［7］ 邹振，刘洪，刘红伟.Kirchhoff叠前时间偏移角度道集［J］.地球物理学报，2010，53(5):1207.

［8］ 滕人达，刘青昆.CUDA、MPI和OpenMP三级混合并行模型的研究［J］.微计算机应用，2010，31(9):63.

［9］ 李博，刘国峰，刘洪.地震叠前时间偏移的一种图形处理器提速实现方法［J］.地球物理学报，2009，52(1):245.

［10］ 李肯立，彭俊杰，周仕勇.基于CUDA的Kirchhoff叠前时间偏移算法设计与实现［J］.计算机应用研究，2009，26(12):4474.

TP332

A

1001—1749(2011)05—0568—04

国家高技术研究发展计划(863计划)(2009AA01A140)

2011－03－22 改回日期:2011－06－19

张慧宇(1983－)，女，硕士，现从事石油物探应用软件研究与开发。