基于角度部份叠加地震数据的流体识别技术

张广智，郑静静，印兴耀，陈怀震

(中国石油大学 地球物理系，山东 青岛 266555)

基于角度部份叠加地震数据的流体识别技术

张广智，郑静静，印兴耀，陈怀震

(中国石油大学 地球物理系，山东 青岛 266555)

角度部份叠加地震数据是对叠前和叠后两种数据的优点进行了折中，既具有相对较高的信噪比，又保留了丰富的信息量，所以从角道集出发研究流体识别和储层预测，能够更加准确、可靠。这里以Zoeppritz方程的Shuey近似为基础，借鉴Smith提出的流体因子表示方法，提出了三种流体识别和储层预测的方法与技术，从而为油藏精细描述提供较为可靠的依据。应用模型和实际数据对作者提出的方法进行了验证，结果证明了本方法可以有效地预测储层，识别流体。

角度部份叠加数据;流体因子;流体识别;Curvelet变换

0 前言

随着勘探难度的加大，对储层预测的精度要求越来越高，需要更有效地预测储层的方法和技术。常规地震属性分析是建立在叠后地震数据基础上的，叠后地震资料在经过多次叠加后，信噪比有了较大的提高，但同时也损失了大量的振幅信息。叠前地震数据与叠后地震数据相比，包含着更加丰富的振幅和旅行时信息，能更灵敏地反映地下油气藏的变化，但是受噪音的影响较大，信噪比不高。角度部份叠加地震数据对两种数据的优点进行了折中，既有相对较高的信噪比，又保留了丰富的信息量。因此，从叠前角道集部分叠加地震数据出发，研究识别流体和预测储层的技术具有很高的实际应用价值。

角道集数据是由叠前CMP道集数据转换而来的，作者在本文从角道集部份叠加数据出发，来研究识别流体和预测储层的有效方法和技术。

作者以Zoeppritz方程的Shuey近似［1］为基础，直接将角道集部份叠加数据认为是流体属性(这可以由Smith和Gidlow［2］的流体因子公式得出)，由其直接进行各种运算，以突出目的层处的异常，达到流体识别的目的。

1 基本原理

1.1 快速的估计波阻抗反射系数的方法

在AVO研究中，纵波、横波阻抗反射系数是流体识别和岩性预测的基础。叠前参数都可以由这两个参数直接或者间接计算得到，并且许多流体因子公式都是这两个参数的函数。因此，在岩性预测和流体识别中，这两个参数的求解就显得尤为重要。

由Zoeppritz方程的 shuey简化式［1］的假设条件可知，当入射角为中等时(0°＜θ≤30°)，Zoeppritz方程可以简化为两项的形式，即

其中 第一项P为θ=0°时的反射系数，称为AVO的截距;G为与岩石纵、横波速度和密度有关的项，称为AVO的梯度。

这样在角度叠加道集中，任意选择两个道集数据，组成方程组，就可以求出截距P和梯度G。例如，

这里 θ1和θ2为入射角;R1、R2分别为相应的反射系数。

公式(2)也可以写成以下形式:

其中 Rp为纵波阻抗反射系数;Rs为横波阻抗反射系数。

可以看出，不同角度的反射系数，可以被看成是Rp和Rs的线性组合。随着角度的变化，Rp和Rs所占的比重也在变化，如图1所示。

图1 角道集数据中Rp和Rs比重随角度变化示意图The proportion variation of Rpand Rswith angle in angle partial data

在图1 中，“1”、“2”、“3”分别代表小、中、大角度，深色表示Rp在角道集中所占的百分比，浅色表示Rs在角道集中所占的百分比。

从图1中可以看出，随着角度的增大道集数据中Rp比重减小，Rs成份所占比重越来越大。

由公式(3)可以直接推导出纵波、横波阻抗反射系数表达式:

因为角度比较小(一般小于30°)，所以将sinθ的泰勒展开式sinθ≈θ(相对误差小于5%)代入式⑷中，Rp和Rs可近似表示为式(5)与式(6)。

采用三次计算取平均的算法，假设小、中、大三个角度道集的角度 θ1、θ2和 θ3满足 θ2=2θ1、θ3=3θ1，则得到如下估算公式:

为方便计算，式⑺与式⑻可以用Rp和Rs的相对大小表示(令R1的系数为1):

公式(10)中的系数α和β，是随着小角度的入射角θ1变化的，其变化规律如表1所示。

表1 公式(10)中α和β随角度的变化Tab.1 Thevariationofα and β withangleinequation10

1.2 基于角道集部份叠加地震数据的新流体识别属性提取

Smith和Gidlow［2］提出了应用流体因子角识别流体的方法。流体因子角(fluidfactorangle)θf就是当储层为含水砂岩时，Shuey(1985)两项近似式的反射系数为零时的入射角。此时，流体因子是在含油气情况下，当入射角为流体因子角度θf时的反射系数值，可以用流体因子角和截距P、梯度G的函数表示流体因子:

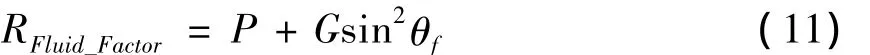
式(11)显示储层含水时，流体因子为零。从公式(1)和公式(11)的对比可知，Smith和Gidlow(2003年)提出的以流体因子角表示的流体因子(RFulid_Factor)是Shuey近似的特殊情况。公式(11)将流体因子属性与入射角，即角道集剖面联系了起来。鉴于此，作者提出了直接应用常规角道集的各种组合进行储层预测和流体识别的方法。经比较发现，角道集部份叠加数据直接相乘，具有与上述流体因子相似的作用，并且可以增大不同流体储层之间的差距，从而更好地预测储层。

1.3 基于曲波变换和贝叶斯理论的流体识别技术

1.3.1 角度流体道集

公式(12)就是直接应用角度道集进行流体识别的理论依据。

当消除子波随角度变化的影响之后，任意两个角度道集的差，是与AVO梯度有关的量，反映了振幅随入射角的变化量，此道集主要反映流体的变化，所以我们命名为角度流体道集。

1.3.2 角度部份叠加数据体预处理

不同角度的道集数据反映的是同一位置处的储层信息，它们只是由于叠加角度的不同才引起角道集部份叠加数据之间存在一定的差异。消除非储层位置处的差异，保留储层处的差异是我们要解决的主要问题。

假设子波随着入射角的变化而变化，同时也把不同角度道集上引起非储层差异的影响归于子波，这种子波是一种随角度变化的等效子波。因此，作者首先提取不同角度道集的等效子波，然后将其替换为平均子波，这种方法我们称为角度子波均衡法。具体做法是:

(1)首先从每个角度部份叠加道集中的非储层中开时窗，提取出一个等效地震子波wθ，计算每个等效地震子波的反子波

(3)令不同角度的等效子波的平均子波为w¯(t)，可得预处理后的角道集:

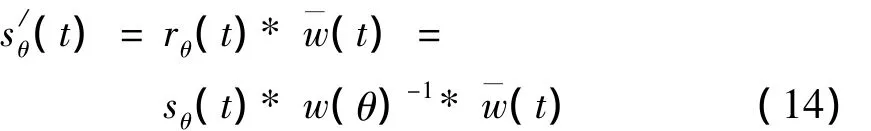
1.3.3 曲波域的贝叶斯波场分离技术

nmxdpath = os.path.join(dirdb , "巴庙镇土地利用总体规划图.mxd")

贝叶斯法的基本思想是:①首先由地质和测井信息得到关于噪声ε和待求参数x的先验分布p(ε)和p(x);②其次用正演模型和p(ε)求出似然函数p(y|x);③再通过贝叶斯公式得到参数的后验分布p(x|y);④最后通过p(x|y)得到关于参数x的信息，流程图如图2所示。

(2)设原始地震数据为 sθ(t)，由 sθ(t)=rθ(t)*wθ得:

图2 贝叶斯参数估计流程图Fig． 2 Flow chart of Bayes' parameter estimation

设地震记录数据s由式(15)给出。

其中 s是大角度地震道集;s1是角度流体道集;s2是均衡后的小角度道集;n是白噪声。

地震信号si可以表示成为曲波的叠加:

其中 A是曲波合成矩阵［3～7］，并获得系统方程，即:

其中 x1是角度流体道集的曲波系数;x2是均衡后小角度数据体的曲波系数;n1和n2是白噪声。

这样，就可以采用贝叶斯理论的后验概率分布函数(PPDF)建立目标函数［8、9］，在曲波域用迭代方法求解模型参数估计值。

在这里假设x1和x2具有的先验分布为Huber分布。由贝叶斯理论可以得到:

应用反复重加权迭代阈值算法，解此最优化问题，可以得到所求曲波系数的迭代公式:

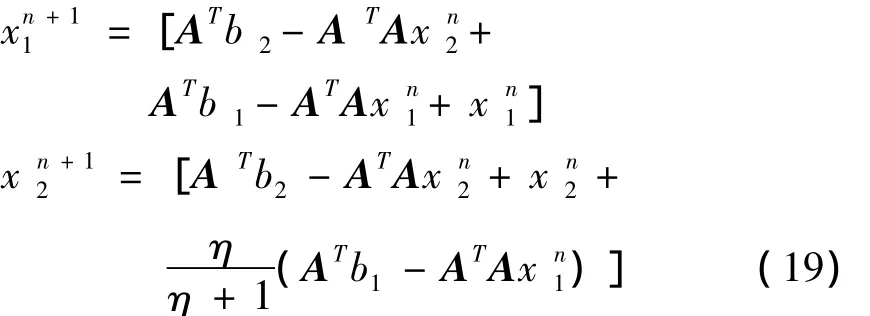
继而，得到角度流体道集的估计值是

1.4 该技术的实现过程

基于角道集部份叠加数据，提取流体属性分为以下几步:

(1)应用公式(7)、公式(8)和公式(9)、公式(10)可以快速准确地估算纵横波阻抗反射系数，将得到的估算值应用到流体因子属性的计算中。例如将估算值代入Fatti［10］提出的流体因子公式或者Smith和Gidlow［2］提出的以流体因子角表示的流体因子属性公式中计算流体因子，得到流体识别的属性值，进行流体识别和储层预测。

(2)将不同的角道集进行相乘运算，得到反映储层流体特征的属性剖面，进行储层预测和流体识别。

(3)角度流体道集的提取以及流体识别:①角度道集预处理，应用前面提出的角度子波互均衡法，以消除非储层在不同角度上的差异，保留由流体引起的不同角度道集上数据的差异;②分离算法构建，这一步关键是构建迭代的分离算法，此方法是稳健的并且能够减小角度子波均衡法中的误差。传统在匹配滤波之后再相减的分离方法，会产生具有残留振幅，调谐，倾角，相位和子波误差的信号预测值。应用曲波域非线性匹配滤波能够改进这种方法的分离值，如果预测信号是位置和倾角的函数，此种匹配法能处理重要的振幅误差;③流体属性的提取，对分离后的流体道集(或者均衡后的角度部分叠加数据)进行各种运算提取叠前地震属性以及反映流体特征的属性，如Rp和Rs属性，G属性以及流体因子属性(应用上面提出的简单公式推导计算得到)，研究它们之间的差异。据此，可以准确地判定储层的位置及范围，为油藏精细描述提供较为可靠的依据。

(4)将三种方法计算结果进行对比分析，预测有利的储层发育带和储层所含流体性质。

2 模型分析

按照上面的方法原理，首先对MarmousiII模型进行了分析，下面给出具体分析结果。为了能够说明问题而计算简单，这里只选取了其中含有两个比较有代表性的储层的一部份，储层分别为含气砂岩层与含油砂岩层(见图3)。

模型中共用到了三个角度的数据，分别为8°、16°、24°。

快速估算纵横波阻抗反射系数的方法及其应用。

图4(见下页)是从MarmousiII模型中抽取的第356道数据，此道分别含有气层、油层和水层。模型的纵、横波速度，密度如下页图4所示，油、气、水所在的位置也已经在图4中标出。

图5(见下页)是应用不同方法估算的Rs和Rp值的比较图。图5(a)表示Rp值，图5(b)表示Rs值。在图5中，圆圈是用上面提出的简单公式估算的结果;星号是应用两项Shuey近似式计算的结果;细线是应用纵波、横波阻抗差计算的精确结果。从图5中可以看出，应用本文的简单公式对Rp、Rs的估算是相当准确的，不论是在储层位置还是非储层位置，以及在气、水层位置和油层位置，都是十分准确的，能够满足生产的要求。

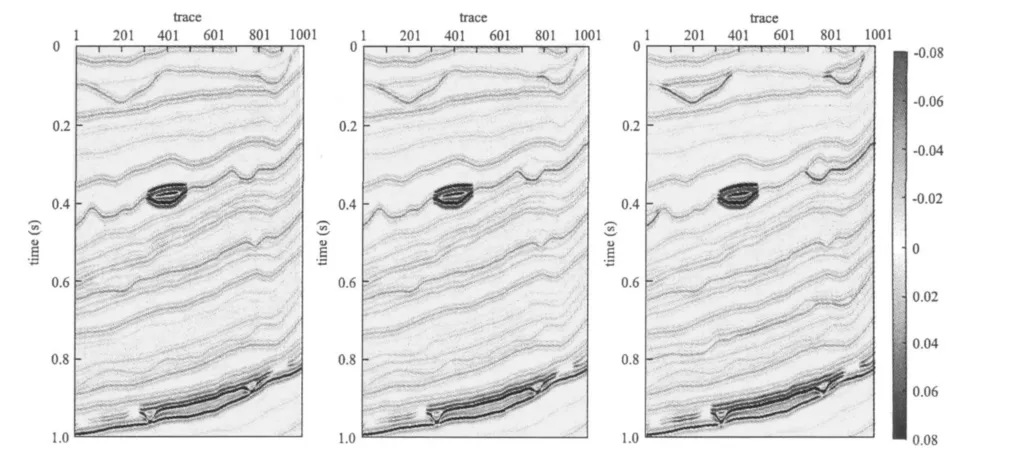
图3 角道集示意图(小角度、中角度、大角度)Fig． 3 Angle data( small，medium and large angle)

图6 (见后面)是应用MarmousiII模型对本方法进行测试的结果。从图5和图6中可以看出，本方法能够比较准确地估算出纵波、横波阻抗反射系数。

图4 MarmousiII模型数据Fig． 4 Marmousi II model

图5 简单近似结果与精确结果的比较Fig． 5 The comparison of simple approximate result and exact result

图7 (见后面)是利用三种方法计算的流体因子属性的对比。图7(a)是利用快速估计波法得到纵波、横波阻抗反射系数，然后将估算值代入流体因子属性计算公式(11)得到属性剖面。图7(b)是应用角度子波均衡法将角道集进行预处理后，利用曲波域的贝叶斯分离技术将角道集分离，得到角度流体道集剖面。图7(c)和图7(d)是应用角道集部分叠加地震数据的组合计算得到流体识别属性剖面。经对比可以看出，三种方法都能比较清楚地刻画储层的位置。

从图7(a)中可以看到，含气(油)和含水储层的差值稍大，因此，第一种方法区别含气(油)和含水储层的能力稍强;如图7(b)所示，第二种方法虽不能够很好地区分含气(油)和含水储层，但可以压制不含流体地层的信息，特别是压制含油储层下方的标志层;图7(c)和图7(d)说明，应用角道集部分叠加地震数据的各种组合得到的属性，可以比较好地区别含气(油)和含水储层，特别是角度道集的三次幂所得到的属性剖面，可以较好地区分含气(油)和含水储层。

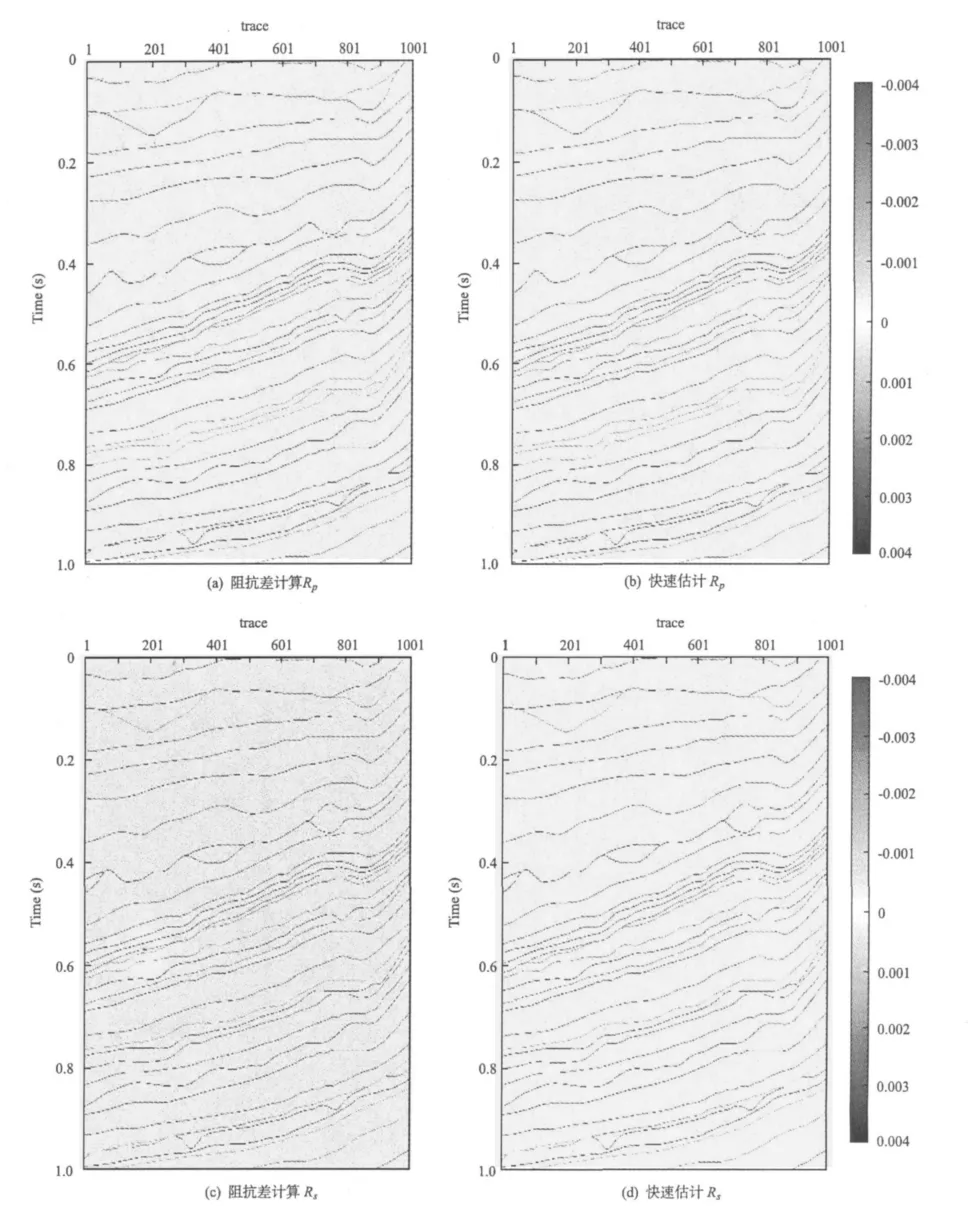
图6 简单计算方法与精确结果的比较Fig． 6 The comparison of simple calculation result and exact result

作者对角度部份叠加地震数据进行了深入研究，提出了三种计算流体因子属性的方法和技术。

(1)应用角度部份叠加地震数据估算纵横波阻抗反射系数，用于常规流体因子属性的计算。

(2)在对流体因子角表示的流体因子公式进行研究以及多次实验的基础上，提出应用角度部份叠加地震数据的各种组合进行流体识别的新方法，并且得到了一系列流体识别的属性。

图7 三种方法计算流体属性比较Fig． 7 The comparison of three methods for calculating fluid attributes

(3)应用曲波变换的多尺度和多方向特性，对角度部份叠加地震数据进行处理，得到角度流体道集，然后再提取反映流体特征的属性。

3 实例分析

根据上述理论，对实际地震数据进行了叠前地震属性提取及分析。首先对角道集数据进行角度子波法预处理，然后从均衡后的角道集数据中提取流体因子。

图8(见下页)为三个角道集剖面。

图9(见后面)为应用三种方法提取的叠前地震属性。从图9(a)中可以看出，应用快速估算波阻抗反射系数的方法得到纵横波阻抗反射系数后，再应用于提取流体因子属性与原始的大角度道集有点相似，这与前面的分析是十分一致的，可以突出储层的位置。如图9(b)所示，应用不同角道集相乘的方法得到的新流体因子属性，能够比较好的突出储层位置，并且对骨架信息有比较好的压制。如图9(c)所示，经过角度子波法预处理和曲波波场分离之后非目的层处的差异减小，从结果中也可以看出曲波波场分离能够突出储层位置。

图8 叠前角度道集Fig． 8 Pre － stack angle data

图9 流体识别属性的比较Fig． 9 The comparison of fluid identification attributes

从对以上模型与实际资料的处理结果中可以看出，从角道集部份叠加数据中提取的地震属性在模型的分析中应用效果较好。从对实际地震数据的分析结果中可以看出，应用方法2和方法3从角道集部份叠加数据中提取出的流体因子属性，能够较清晰地刻画出油气储层的边界。

4 结论

(1)作者在本文从角度部份叠加地震数据出发，进行了一系列的研究，提出三种有效的储层预测和流体识别的方法，这些方法充分利用了角度部分叠加地震数据的优点，以及角度部份叠加地震数据之间的差别。突出了目的层处的异常，提高了流体识别的有效性。

(2)作者直接将角度部份叠加地震数据视为流体属性的方法，打开了流体识别的新思路。利用提出的三种方法互相验证，可以准确地判定储层的位置及范围，为油藏精细描述提供了一种较为可靠的研究思路。

致谢:感谢中国石化集团公司的资助及提供实际数据，感谢 HoustonUniversity提供MarmousiII模型资料的下载。

［1］ SHUEY R T． A simplification of the Zoeppritz equations［J］． Geophysics， 1985( 50) : 609．

［2］ SMITH G C， IDLOW P M． The Fluid Factor Angle［J］．EAGE 65th Conference ＆ Exhibition， 2003: 2．

［3］ CANDES E J． Ridgelets: theory and applications［D］．USA: Department of Statistics， Stanford University，1998．

［4］ CANDES E J，DONOHO D L． New tight frames of curveletsand optimal representations of objects with C2 singularities［J］． Commun． on Pure and Appl． Math，2004， 57( 2) : 19．

［5］ CANDES E J，DEMANET L，Donoho D L，et al． FastDiscrete Curvelet Transforms ［R］． Applied and ComputationalMathematics． California Institute of Technology，2005: 1．

［6］ GUANGZHI ZHANG，JINGJING ZHENG，XINGYAOYIN． Coherence cube based on Curvelet transform［C］:SEG Las Vegas Annual Meeting， 2008: 924．

［7］ 郑静静，印兴耀，张广智.基于曲波变换的多尺度分析技术［J］.石油地球物理勘探，2009，44(5):543.

［8］ 杨培杰，穆星，印兴耀.叠前三参数同步反演方法及其应用［J］.石油学报，2009，2(30):232.

［9］ DANPING CAO，XINGYAO YIN，FANCHANG ZHANG．Joint inversion of 3D seismic，VSP and crosswell seismicdata［C］． SEG Houston Annual Meeting， 2009: 2373.

［10］ FATTI J，SMITH G，VAIL P， et al． Detection of gas insandstone reservoirs using AVO analysis: A3 － D seismiccase history using the geostack technique［J］: Geophysics，1994( 59) : 1362．

P631.4+43

A

1001—1749(2011)05—0467—10

国家重点基础研究计划(973)项目(2007CB209605);国家油气重大专项(2008ZX05014－001－010HZ)

2011－06－08 改回日期:2011－06－21

张广智(1971－)，男，博士，副教授，主要从事地震属性，储层预测和流体识别方面的研究。