矩形线圈自感的精确表达式

武中华，李文尧

(昆明理工大学国土资源工程学院，云南昆明 650093)

矩形线圈自感的精确表达式

武中华，李文尧

(昆明理工大学国土资源工程学院，云南昆明 650093)

矩形线圈的自感公式在电气工程、电工电子技术，以及应用地球物理学等领域均有普遍的应用。由于自感计算的复杂性，目前使用的矩形线圈自感公式均为近似计算公式。这里推导了圆截面单匝矩形线圈自感的精确表达式，以及正方形单匝线圈自感的近似公式。目前使用的单匝矩形线圈自感近似公式与这里推导的精确公式相比，均存在很大误差:当正方形线圈边长从1m到5m时，电气工程工具书和电工电子工具书中的自感公式误差为3.06%到2.38%。使用瞬变电磁法勘探中常用的自感公式，当正方形回线边长为5m时，误差最小为－41.17%，最大为228.25%;当回线边长为200m时，误差最小为－59.75%，最大为212.49%。

矩形线圈;自感;精确表达式

0 前言

矩形线圈的自感公式在电气工程、电工电子技术以及应用地球物理学中均有普遍的应用。在目前的物理学教科书［1、2］中以及物理工具书［3］中，均没有涉及到矩形线圈自感的精确计算公式;在苏联科学家编写的电感计算手册［4］、国内出版的电气工程工具书［5～7］，以及电工电子技术工具书［8］中，矩形线圈的自感计算均为近似公式。在目前的瞬变电磁法教科书［9、10］以及论文［11］中，矩形回线的自感计算均使用近似公式。在国内、外相关专业电磁学领域中，工作者多使用有限元法［12～18］计算复杂电磁场，不存在矩形线圈自感的精确表达式。虽然李文尧等［19］于2010年推导了矩形回线自感计算公式，但该公式的推导过程没有涉及导线的内自感。

作者在本文中，为进一步完善该公式，精确验证现有公式的精度以及误差情况，推导出了在低频条件下，使用的圆截面矩形线圈自感的精确表达式。

1 矩形单匝线圈自感精确表达式

在低频条件下，可以不考虑电流的趋肤效应，认为导线中的电流在截面上成均匀分布，此时由圆截面导线绕制成的矩形线圈的自感应，包括外自感和导线内自感，在本文中作者将分别推导外自感L0和内自感Li的表达式。

1.1 矩形线圈外自感的表达式

设矩形线圈的边长分别为a和b，o— a边位于x轴上，o— b边位于y轴上，如图1所示。根据文献［20］，矩形线圈平面内任意一点的磁感应强度B表达式为式(1)。

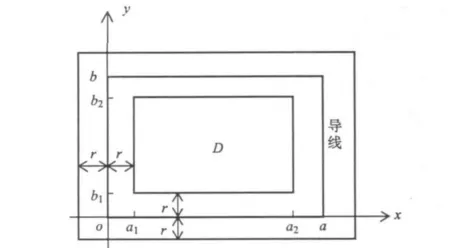
图1 矩形单匝线圈示意图Fig． 1 The schematic diagram of rectangular coilin single-turn

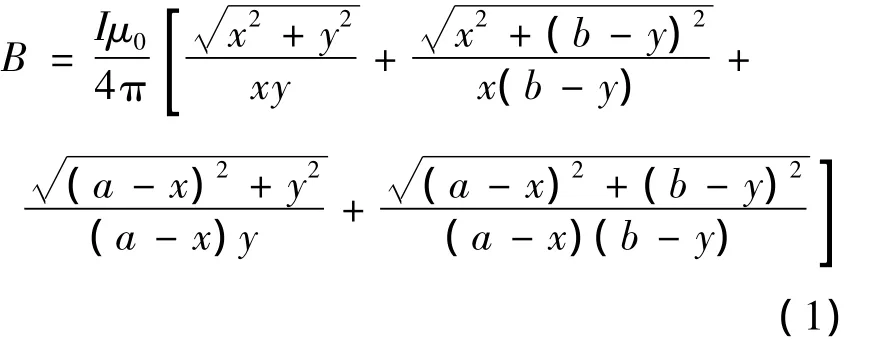
矩形线圈自感的表达式为式(2)。

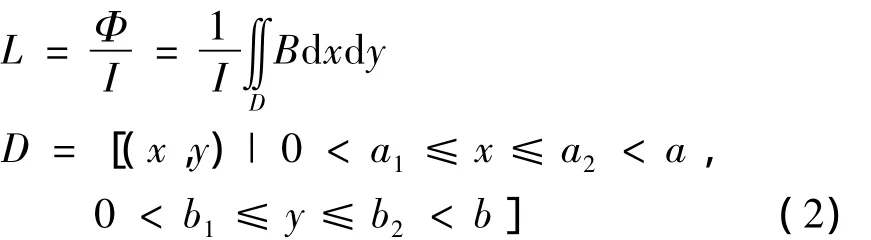
式中 L为自感系数;Φ为磁通量;B为磁感应强度;I为电流强度;μ0为真空中的磁导率(4π×10－7H/m);a、b为回线边长;r为回线半径。

并且a1、b1、a2、b2为积分区域边界点:

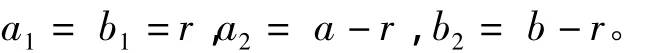
令:

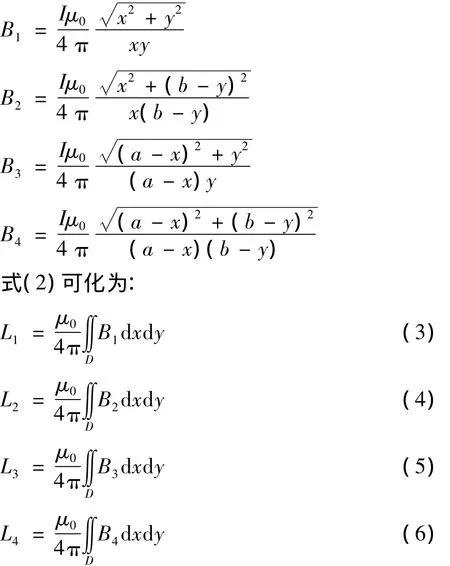
对以上四个二重积分式进行解析推导［19］后，可以得到相应的表达式:

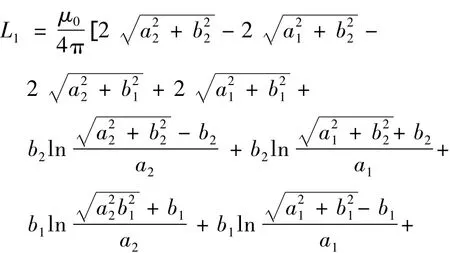
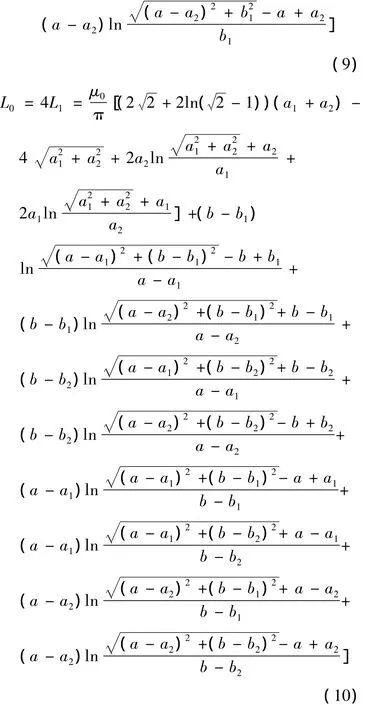
单匝矩形线圈的外自感解析表达式L0为:

若矩形线圈的平面布置为正方形，即 D=［(x，y)|0 ＜a1≤x，y≤a2＜a］，则可以得到单匝正方形线圈外自感的解析表达式:

当边长a远远大于导线半径r时，式(12)分子中的微小变量a1、a2趋近于零，a2趋近于a，得到正方形单匝线圈外自感的近似公式:

式中 a为正方形线圈边长;r为导线半径。

1.2 圆截面直导线内自感的表达式

根据安培环路定律［3］:

式中 μ为导线的磁导率;I’为通过以r为半径的圆平面的电流，取

图2 圆截面直导线示意图Fig． 2 The schematic diagram of circular section wire

见图2，与圆截面导线同轴的圆柱面上任一点的磁感应强度为:

根据磁感应强度与磁场强度的关系:B=μH，可以得到:

磁能公式为:

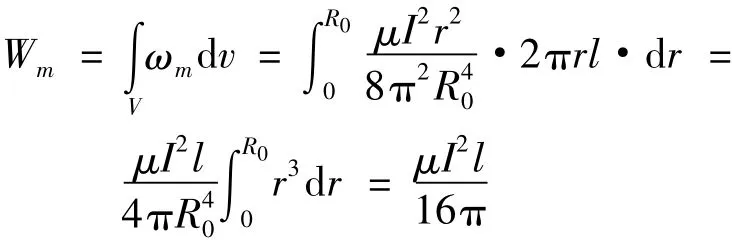
式中 l为导线长度。

根据自感与磁能关系式:

得到内自感表达式［21］为式(14)。

1.3 圆截面矩形线圈自感的表达式

由圆截面导线绕制成的矩形线圈自感精确表达式为:

当线圈为正方形时，自感公式变为:

同时，可以得圆截面正方形线圈自感近似公式(17)。

式中 μr为相对磁导率。

2 将推导的自感精确表达式与目前使用的公式比较

当导线的材料［20］不同时，μr不同，产生的自感也不同。导线材料为抗磁质和顺磁质时，μr≈1，只用当导线材料为铁磁质(包括铁、钴、镍、某些稀土元素以及铁氧体等)时，才会有 μr≫1。以下的对比试验，作者均采用铜导线，此时可认为μr=1。

2.1 与电气工程和电工电子技术中使用的公式比较

电气工程［5～7］和电工电子技术［8］使用的单匝矩形线圈自感公式为式(18)。

其中 r0为导线半径;a、b为线圈边长;d为矩形线圈的对角线长。

当线圈为正方形时，式(18)可化简为式(19)。

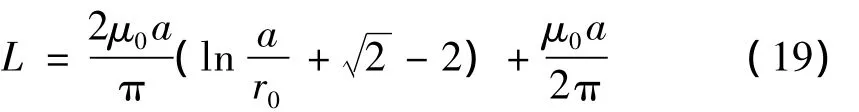
设半径r0=0.001m的铜质导线，绕制成边长a分别为1m、2m、3m、4m、5m的正方形单匝线圈，使用式(18)，作者推导精确公式(15)以及使用作者推导近似公式(17)，计算自感值及误差。结果见表1。

计算结果表明:

(1)当正方形单匝线圈边长从1m到5m时，使用公式(18)计算的自感值误差为3.06%到2.38%，并且误差随线圈边长减小而增加。

(2)当正方形单匝线圈边长从1m到5m时，使用作者推导的自感近似计算公式(17)计算的自感值误差为－0.41%到－0.39%。

表1 电气工程中使用的自感公式与本文推导公式对比Tab． 1 Comparison calculation with self － inductance formula in electrical engineering

2.2 瞬变电磁法中使用的自感计算公式

根据文献［9］及［11］，正方形单匝线圈自感的近似计算公式为:

其中 L为自感;b为回线边长;r为导线半径。

若以回线中心点的磁感应强度代表回线的平均磁感应强度时，正方形回线自感的近似表达式为:

式中 L为自感;b为回线边长。

根据文献［10］，长方形回线自感的近似计算公式为式(22)。

其中 L为自感;a、b分别为长方形回线的边长。

设半径r0=0.001m的导线，绕制成瞬变电磁法勘探中常用规格的正方形单匝线圈，边长a分别为5m、10m、25m、50m、100m、200m。使用本文推导精确公式(15)，近似公式(17)，以及文献中的近似公式(20)，式(21)以及式(22)，计算自感值及误差，结果见表2。

计算结果表明:

(1)目前，在瞬变电磁法中使用的矩形线圈自感近似公式误差很大:当回线边长为5m时，误差最小为－41.17%，最大为228.25%;当回线边长为200m时，误差最小为 －597.75%，最大为212.49%。

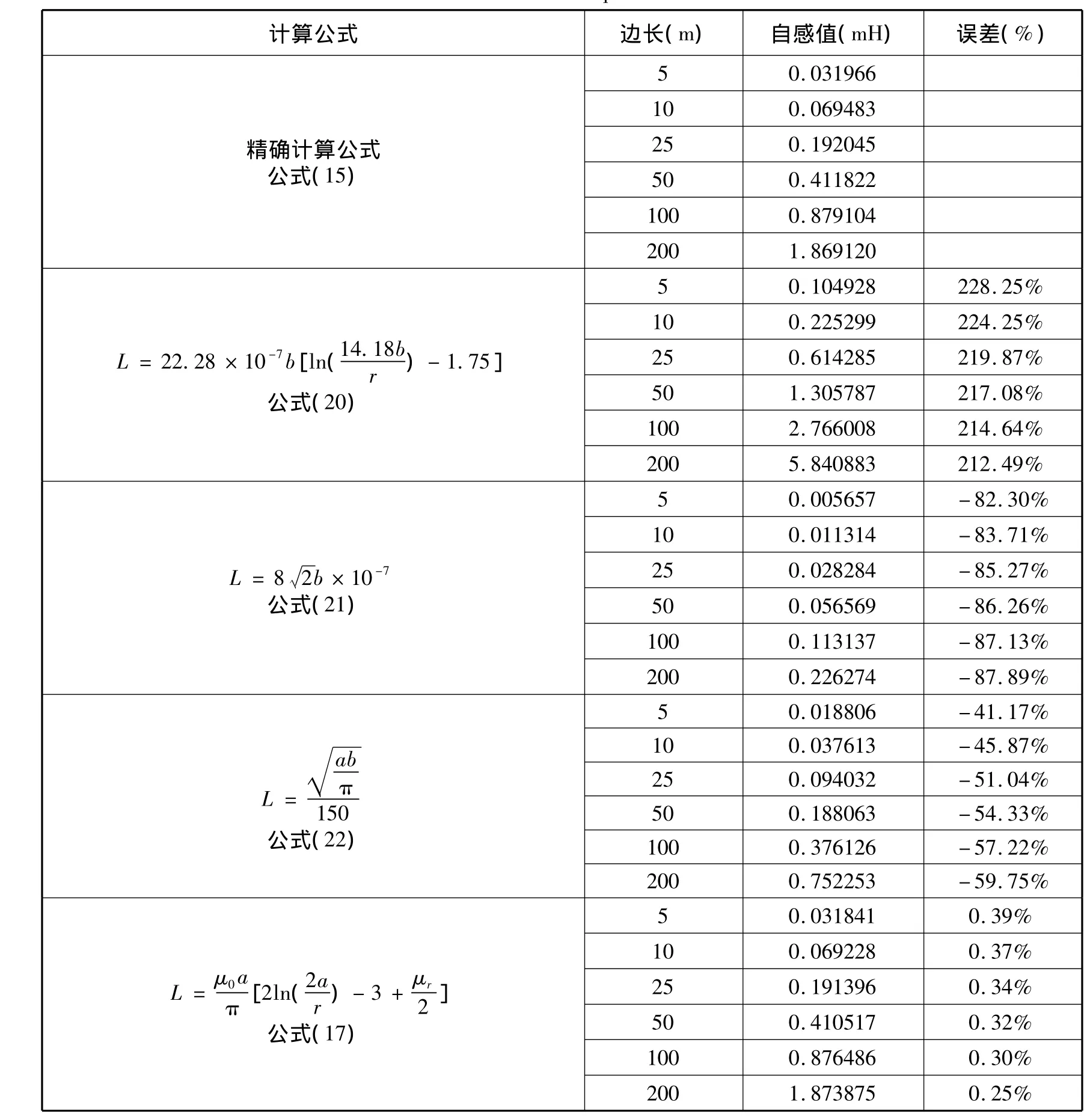
表2 野外常用正方形线圈的自感计算结果Tab． 2 Calculation of self-inductance coefficient of square coil of sizes in common use in outdoors

(2)作者在本文中导出的单匝正方形线圈自感近似公式误差很小:当回线边长大于5m时，误差小于0.39%;随回线边长增大，误差递减。

3 结论

(1)作者在本文推导了的长方形及正方形圆截面单匝线圈自感精确表达式，分别为公式(15)和公式(16)，并导出了正方形圆截面单匝线圈自感近似公式(17)式。

(2)与作者在本文中所推导的自感精确表达式相比，目前在电气工程和电工电子技术中，使用的圆截面矩形线圈自感近似公式存在误差，建议使用作者在本文推导的精确公式(15)和式(16)以及近似公式(17)。

(3)与作者推导的自感精确计算公式相比，目前在瞬变电磁法中使用的矩形线圈自感近似公式误差很大，在瞬变电磁法勘探工作中建议少用或者不用。作者推导的近似公式误差很小，在瞬变电磁法中建议使用。

［1］ 马文蔚.物理学(第五版)［M］.北京:高等教育出版社，2006.

［2］ GERALD L，POLLACK，DANIEL R． Stump． Electronmagnetism［M］． Higher Education Press， 2005

［3］ HORSTSTOCKRE.物理手册(第一版)［M］.吴锡真，译.北京:北京大学出版社，2004.

［4］ 卡兰塔罗夫，采伊特林.电感计算手册［M］.陈汤铭，译.北京:机械工业出版社，1992.

［5］ 王建华.电气工程师手册(第三版)［M］.北京:机械工业出版社，2008.

［6］ 王兆安，张明勋.电力电子设备和应用手册(第三版)［M］.北京:机械工业出版社，2009.

［7］ 周鹤良.电气工程师手册［M］.北京:中国电力出版社，2008.

［8］ 吕砚山.常用电工电子技术手册［M］.北京:化学工业出版社，1995.

［9］ 蒋帮远.瞬变电磁法勘探［M］.北京:地质出版社，1998.

［10］ 牛之琏.时间域电磁法原理［M］.长沙:中南工业大学出版社，1992.

［11］ 薛国强.论瞬变电磁测深法的探测深度［J］.石油地球物理勘探，2004，39(5):575.

［12］ 刘国强，赵凌志，蒋继娅.工程电磁场有限元分析［M］.北京:电子工业出版社，2005.

［13］ NANNAPANENI NARAYANA RAO． 工程电磁学基础( sixth edition) ［M］． 周建华，译． 北京: 机械工业出版社， 2006．

［14］ SIJOY C D，CHATURVEDI S． Calculation of accurateresistance and inductance for complex magnetic coils usingthe finite － difference time － domain technique forelectromagnetics［J］． IEEE TRANSACTION ON PLASMASCIENCE， 2008， 36( 1) : 70．

［15］ JAN K RAINEY，JEFFREY S DEVRIES，BRIAN DSYKES． Estimation and measurement of flat or solenoidalcoil inductance for radiofrequency NMR coil design［J］． Journal of Magnetic Resonance，2007，187 ( 1) :27．

［16］ CHRISTISAN PETERS，YIANNOS MANOLI． Inductancecalculation of planar multi － layer and multi － wirecoils: An analytical approach［J］． Sensors and Actuators，2008，A 145 － 146: 394．

［17］CHRISTIAN HARLANDER， RAINER SABELKA，SIEGFRIED SELBERHERR． Efficient inductance calculationin interconnect structures by applying theMonte Carlo method［J］ ． Microelectronics Journal，2003， 34: 815．

［18］ M． R． ALIZADEH PAHLAVANI，A． SHOULAIE． Anovel approach to calculate inductance and analyzemagnetic flux density of helical toroidal coil applicableto Superconducting Magnetic Energy Storage systems( SMES) ［J］． Physica C 470， 2010: 391．

［19］ 李文尧，武中华.瞬变电磁法矩形线圈自感的精确表达式［J］.地质与勘探，2010.46(1):160.

［20］ 张秋光.场论上册［M］.北京:地质出版社，1983.

［21］ 俞大光.电工基础下册［M］.北京:人民教育出版社，1961.

TM55

A

1001—1749(2011)05—0511—06

2011－04－11

武中华(1985－)，男，辽宁朝阳人，硕士，地球探测与信息技术专业。