基于非结构化网格的瞬变电磁2.5维有限元正演模拟

赵晓博，朱自强，李建慧，彭凌星

(中南大学 地球科学与信息物理学院，湖南长沙 410083)

基于非结构化网格的瞬变电磁2.5维有限元正演模拟

赵晓博，朱自强，李建慧，彭凌星

(中南大学 地球科学与信息物理学院，湖南长沙 410083)

利用Delaunay三角化这种网格非结构化方法，通过编程实现了二维模型的非结构化三角形网格剖分，并编写了中心回线法瞬变电磁2.5维有限元正演程序。与前人计算结果对比，在取得相同计算精度的情况下，与结构化网格相比，非结构化网格所需网格和节点数量大大减少，计算效率更高。通过将非结构化网格法引入到瞬变电磁2.5维正演模拟中，实现了对复杂二维地电模型的有限元数值模拟，提高了现有有限元算法的应用范围。

非结构化网格;Delaunay三角化;瞬变电磁;有限单元法

0 前言

瞬变电磁法是一种时间域电磁勘探方法，已广泛应用于能源、矿产、水文、工程、环境等领域。目前，瞬变电磁法资料解释水平较低，基本上停留在一维阶段，而二维或三维瞬变电磁反演在解释技术方面仍处于探索研究阶段，离真正实用阶段仍有相当大的距离［1、2］。由于正演是反演、资料解释的基础，所以开展瞬变电磁法的正演研究很有必要。

2.5 维正演模拟是在实际中应用较多的一种正演模型，与三维模型相比，2.5维正演模拟只需对截面而不是整个体积作离散处理，节省了计算量。同时，与一维、二维模型相比，2.5维正演模拟又能较好的近似地质情况。

目前，国内、外对于人工源电磁场的2.5维有限元数值模拟已做了大量研究，并取得了丰硕的成果，但基本上是基于结构化网格实现的［3～10］。结构化网格在人工源电磁场问题的数值模拟中，有下面两个缺点:

(1)结构化网格的几何适应能力通常较差，因此对于较复杂计算区域，很难控制网格节点的分布情况，并会产生较大的离散误差，从而影响有限元计算精度。

(2)结构化网格很难处理网格的疏密过渡。而在电磁场的有限元正演模拟中，要做一些微分运算，需要对局部做网格加密处理，这时使用结构化网格就必须将网格划分得足够小，从而使节点数大大增加，增加了不必要的计算量，影响了有限元计算速度［11、12］。

而相对于结构化网格，非结构化网格对复杂区域边界和约束情形有很强的适应能力，可以更好地适应不规则计算区域和快速实现网格生成自动化，在网格生成中也只需要对异常区和测点处做加密处理。因此，利用非结构化的网格剖分，可以提高有限元计算的精度，同时也方便对不规则异常体的模拟。

本文作者通过编程实现了二维模型的非结构化网格剖分，针对实际生产中常用的中心回线模型，编写了瞬变电磁2.5维问题的有限元正演程序。通过程序计算表明，在取得相同计算精度的情况下，与结构化网格相比，非结构化网格所需网格和节点数量大大减少，计算效率更高。另外，采用非结构化网格，容易实现复杂二维地电模型的数值模拟，也可以提高现有有限元算法的应用范围。

1 2.5维瞬变电磁法的有限元法

对于一个如图1所示的中心回线瞬变电磁2.5维问题，它是一个关于 (x，y，z，t)的四维电磁场问题。对时间变量t作拉普拉斯变换，对走向y方向做傅里叶变化，可将此连续的四维电磁场问题降维为离散的频率波数域中的关于x、z方向的二维问题。通过一系列的公式推导，可将频率波数域中的中心回线法瞬变电磁场2.5维边值问题表示如下［8］:

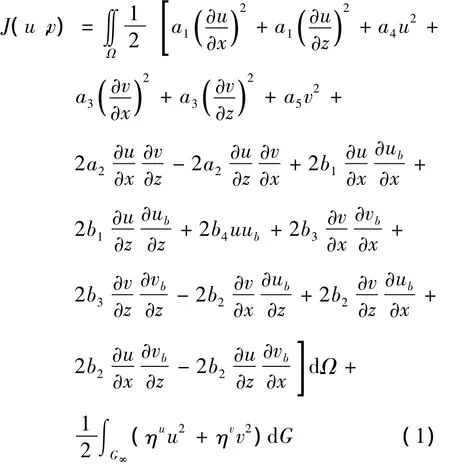
在这里:ub=eb，y

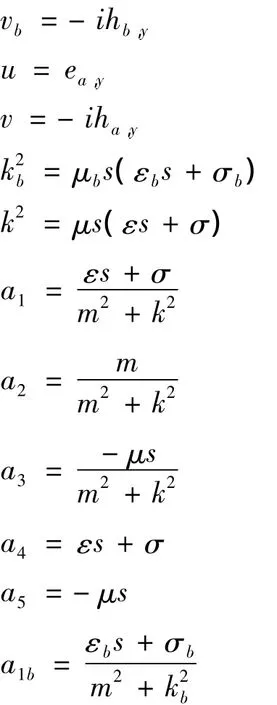
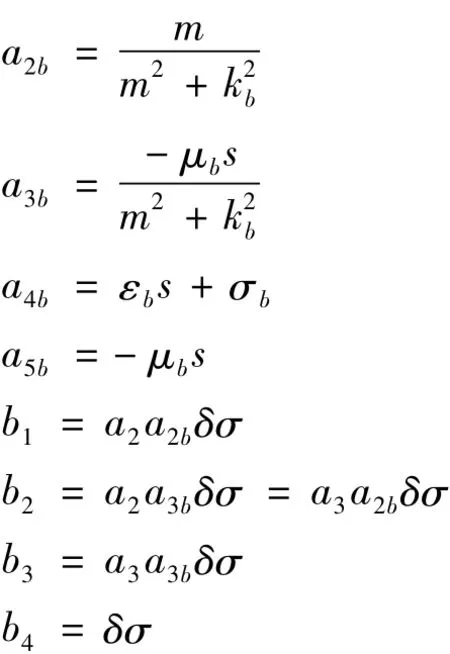
其中 Ω为求解区域;G为求解区域外边界;eb，y、hb，y与 ea，y、ha，y分别为频率波数域中电、磁场的走向分量的背景场、异常场;m为离散的波数集;s为离散的频率集;k为介质的传播系数;ε、μ、σ分别为介质的介电常数、磁导率和电导率，δσ=σσb为相对异常电导率。

对式(1)通过区域剖分(文中采用三角形网格)、线性插值、单元分析、总体合成、求变分等步骤，便可得到关于变分问题式(1)的线性方程组，详细过程可参见文献［9］，这里不再赘述。

解此线性方程组，便可求得频率波数域中的各节点u、v值。

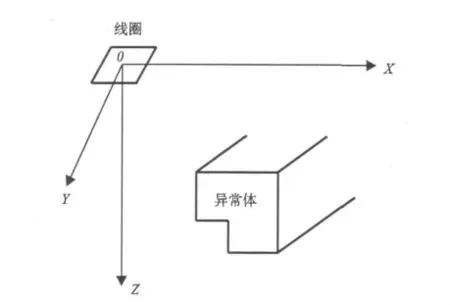
图1 中心回线瞬变电磁2.5维问题示意图Fig. 1 The schematic diagram of 2. 5 － D TEM witha central loop

2 测点感应电动势计算

通过有限元计算求得的u、v值，为频率波数域中异常体走向分量的电场、磁场异常场的场值，可根据式(2)求得频率波数域中z分量的磁场异常场场值［8］:

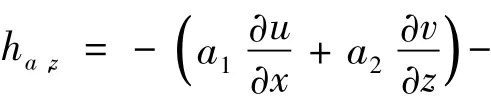
再对ha，z反拉氏变换和反傅氏变化之后，便可求得给定点空间异常场分量的瞬变响应Ha，z(t)。

根据式(3)，可求得异常场形成的感应电动势εa(t)。

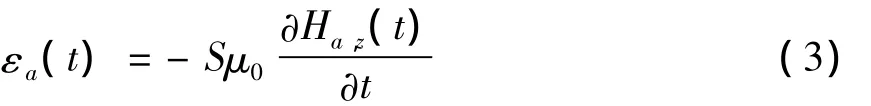
式中 S为接收线圈的等效面积;μ0为真空中的磁导率。

根据式(4)，可计算出我们平常测量中所关心的总场感应电动势ε(t)。

其中 εb(t)为背景场形成的感应电动势。

3 非结构化网格法

网格可分为结构化和非结构化两类。结构化网格，每个内部节点都被相同数目的单元所包含;而非结构化网格中，包含每个内部节点的数目是不相同的。

Delaunay三角化方法是目前应用较为广泛的非结构化网格生成方法。Delaunay三角化方法是将平面上的一组已经给定的点联结成三角形，并具有以下特点:

(1)形成的三角形互不重叠。

(2)可以覆盖整个计算区域。

(3)每一个点均在不包括该点的三角形的外接圆外。

Delaunay三角化方法具有以下优点:

(1)用Delaunay三角化方法连接成的三角形，能取得最大的最小角。这意味着，对给定的一组点，用Delaunay三角化方法生成的三角形的边长均匀性是最好的。

(2)Delaunay三角化方法生成的网格，在空间上是全局优化的结构，能满足高精度计算中需要网格尽量饱满的要求，而且可以方便地对已经生成的网格进行加点和减点操作并保证新生成的网格仍然是Delaunay网格。

而一般的三角网格并不具备这些优点［13、14］。

Delaunay算法分为下述两个步骤。

3.1 边界网格的初始化

生成一个包含所有给定边界点集P0的大三角形T0。∀P∈P0，将外接圆包含P的所有三角形找出，记下这些三角形形成的边界，并删除这些三角形。将点P与空洞边界上每一边连接，形成新的三角形，将新生成的三角形加入三角形集合T中，并将点P从边界点集合P0中删除。

重复上述操作，直到集合P0为空。将所有包含T0顶点的三角形从集合T中删除。

3.2 内部结点的自动生成

在三角形集合T中，寻找外接圆半径最大的三角形，在其外接圆心处加入点P。寻找外接圆包含P的所有三角形，将点P与删除这些三角形后所形成的空洞边界上每一边连接形成新的三角形，并将新生成的三角形加入集合T中。对现存三角形按外接圆半径大小排序，最大的在序列的顶上。

重复上述步骤，直到集合T中三角形的最大外接圆半径，小于某一给定值即可终止迭代。

4 正演算例

4.1 H型模型

H型三层地电断面模型的参数为 ρ1=100Ω·m、h1=100m、ρ2=20 Ω·m、h2=100m、ρ3=100Ω·m。采用中心回线装置，发送回线边长50m，接收线圈等效面积50m2，供电电流1A。

图2(见下页)为采用非结构化网格剖分的有限单元解与解析解的对比图。

表1为非结构化网格计算效果与熊彬［9］采用的一个矩形网格中细分为四个三角形网格的计算效果作的对比。由表1可以看出，在取得大约同样计算精度的情况下，非结构化网格所需单元数和节点数，远远少于结构化网格所需，因而大大提高了计算效率。

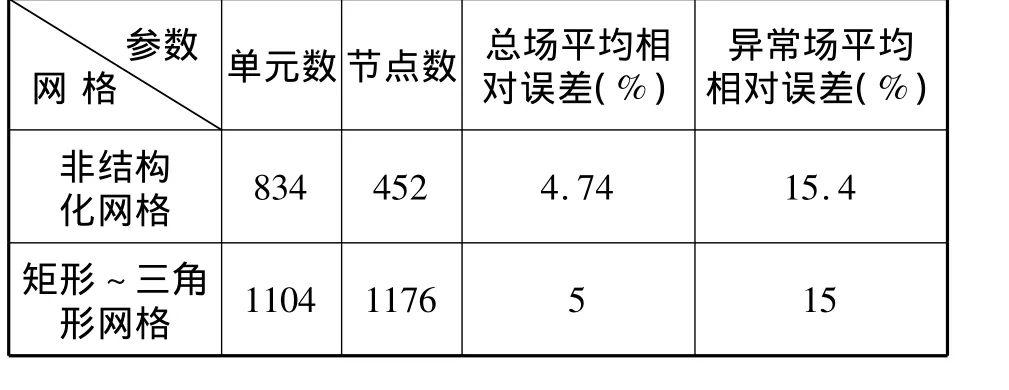
表1 H型模型非结构化网格与结构化网格计算效果对比Tab. 1 The computational efficiency comparison of unstructuredgrid and structured grid for H － model

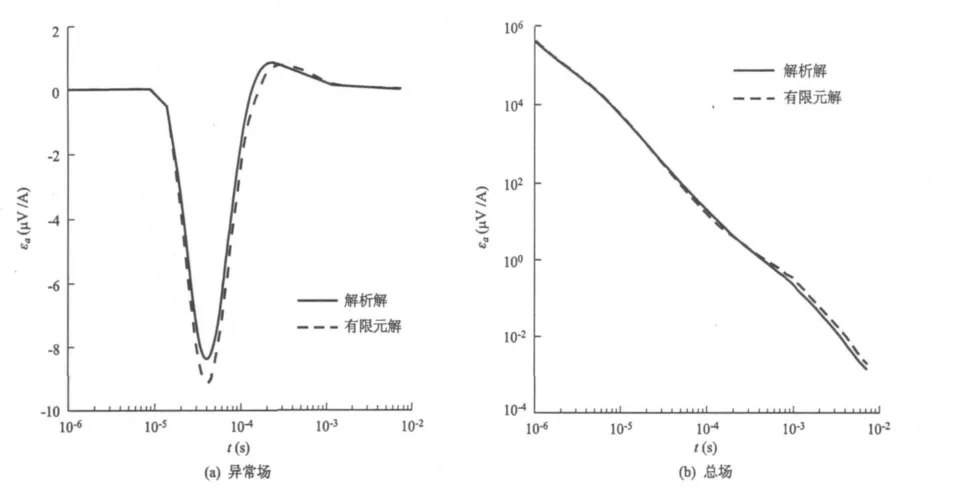
图2 H型模型2.5维有限元法解与解析解曲线对比图Fig. 2 The comparison of 2. 5D FEM solution and analytical solution for H － model

4.2 低阻圆柱体模型

模型如图3所示，电阻率为100Ω·m的围岩中有个沿一方向无限延伸的电阻率为0.5Ω·m的圆柱体，圆柱体半径为50m，中心点埋深为100m。采用中心回线装置，发送回线边长50m，接收线圈等效面积50m2，供电电流1A。

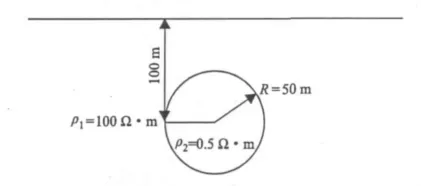
图3 圆柱体模型图Fig.3 Themodeldiagramofcylindricalbody

图4 为测点位于圆柱体正上方时，此模型对应的非结构化网格剖分结果图。在有限元计算中，与结构化网格只需一次剖分不同的是，采用非结构化网格当测点移动时，网格需要重新剖分。为了提高计算精度，作者在测点和异常体附近均作了网格加密。

下页图5(a)为低阻圆柱体模型的瞬变电磁测深剖面图。由图5(a)可见:①在1.0×10－6s～2.4×10－5s期间，各测道的剖面曲线都很平缓;②在3.6×10－5s～9.6×10－5s期间，各测道出现对称与球顶的低谷异常;③在9.6×10－5s之后，各测道均呈现明显的对称与球顶的单峰异常，与物理模拟结果一致［15］。下页图5(b)为低阻圆柱体模型不同测点处的异常曲线，图5(b)中dx表示测点距圆柱体中心点地面投影处的距离。从图5(b)中可以看出，当dx=0m(测点位于圆柱体中心正上方)时，异常曲线幅值最大。随着dx的增大，异常幅值逐渐衰减，并逐渐趋近于均匀半空间的场值。

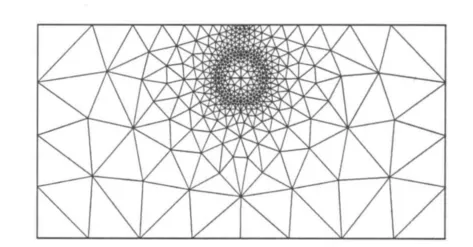
图4 测点位于圆柱体中心地面投影点处时模型非结构化网格剖分图Fig. 4 Unstructured mesh of the model when the measuringpoint at cylindrical center's projection point on theground

5 结论

利用非结构化网格，是模拟复杂二维地质体瞬变电磁响应的一种新工具。利用非结构化网格，可允许数值模型中包含复杂二维地质体，这是传统的结构化网格所不能做到的。因此，作者在本文的研究对提高现有瞬变电磁2.5维有限单元算法应用范围有很好的意义。

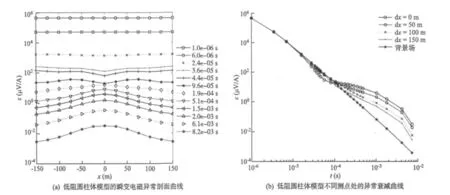
图5 低阻圆柱体模型有限元法数值模拟结果Fig. 5 The FEM numerical simulation result of low resistance cylindrical body model

通过非结构化三角形网格代替传统的结构化网格，对地电断面做剖分，对异常区和测点附近做加密处理，在拟合地电断面的情况下，尽可能地减少了不要的网格的生成。通过文中程序计算表明，在计算精度相当的情况下，采用非结构化网格比结构化网格所需单元数和节点数大大减少，因此可以大幅减少计算资源，提高了计算效率。

［1］ 吕国印.瞬变电磁法的现状与发展趋势［J］.物探化探计算技术，2007，29(增刊):111.

［2］ 薛国强，李貅，底青云.瞬变电磁法正反演问题研究进展［J］.地球物理学进展，2008，23(4):1165.

［3］UNSWORTH M J，TRAVIS B J，CHAVE A D. Electromagneticinduction by a finite electric dipole source overa 2－D earth ［J］. Geophysics，1993，58( 2) : 198.

［4］YONFLIANG MENG，WEIDONG Li， MICHAEL S.ZHDANOV，et al. 2. 5 － D electromagnetic forwardmodeling in the time and frequency domains using the finiteelement method SEG'69 Annual Meeting ExpandedAbstracts［M］. Tulsa: Society of Exploration Aeophysicists，1999.

［5］ MITSUHATA Y. 2 － D electromagnetic modeling by finite－ element method with a dipole source and topography［J］. Geophysics，2000，65( 2) : 465.

［6］ KONG F N， JOHNSTAD S E，RØTEN T，et al. A 2.5D finite － element modeling difference method for marineCSEM modeling in stratified anisotropic media ［J］.2008， 73( 1) : F9.

［7］ XIONG B. A new formula based on the independent electricand magnetic fields for 2. 5 － D forward of TEM［Z］. The 19th international workshop on electromagneticinduction in the earth，2008: 536.

［8］ 王华军，罗延钟.中心回线瞬变电磁法2.5维有限单元算法［J］.地球物理学报，2003，46(6):855.

［9］ 熊彬，罗延钟.电导率分块均匀的瞬变电磁2.5维有限元数值模拟［J］.地球物理学报，2006，49(2):590.

［10］底青云，MARTYNUNSWORTH，王妙月.有限元法2.5维CSAMT数值模拟［J］.地球物理学进展，2004，19(2):317.

［11］任政勇，汤井田.基于局部加密非结构化网格的三维电阻率法有限元数值模拟［J］.地球物理学报，2009，52(10):2627.

［12］汤井田，王飞燕.基于非结构化网格的2.5D直流电阻率模拟［J］.物探化探计算技术，2008，30(5):413.

［13］陈建军.非结构化网格生成及其并行化的若干问题研究［D］.杭州:浙江大学博士论文，2006

［14］肖根如，甘卫军，陈为涛.地应变计算Delaunay三角网在MATLAB与GMT环境下的相互转换［J］.大地测量与地球动力学，2010，30(3):122.

［15］李金铭.地电场与电法勘探［M］.北京:地质出版社，2005

P631.3+25

A

1001—1749(2011)05—0517—05

2011－02－18 改回日期:2011－06－19

赵晓博(1985－)，男，甘肃正宁人，硕士，主要从事瞬变电磁法理论研究。