三端直流输电系统大地金属回线转换策略
刘 航,黄曼茜,彭茂兰,王海军,许建中,张怿宁
(1. 超高压输电公司 检修试验中心,广东 广州 510663;2. 华北电力大学 新能源电力系统国家重点实验室,北京 102206)
0 引言
为提升设备可用率、减少输电线路投资,长距离直流输电系统多采用“真双极+接地极”架构[1-4]。以两端直流输电系统为例,正常情况下,两站以双极大地回线运行,极平衡时,入地电流可以忽略,单极故障工况下,随着故障极的退出,接地极将流过额定电流,为避免较大入地电流对油气管网产生影响,需要及时将在运极转为单极金属回线运行。此外,故障极恢复后,需要及时将在运极转回单极大地回线运行,以重新投入另一极。因此直流输电系统需要具备大地、金属回线自由转换的能力。
对于两端直流输电系统,只需在任一站配置转换开关,通过分合转换开关即可完成大地、金属回线转换。而对于三端直流输电系统,由于第三站不能独立地运行于其他回线(无法构成回路),大地、金属回线转换需3站协调进行,将3站一并转为金属回线或大地回线。因此就大地、金属回线转换的复杂性而言,三端直流输电系统要高于两端直流输电系统。
针对两端直流输电系统,文献[5]分析了直流转换开关的工作原理及工况,文献[6-11]对回线转换的暂稳态过程及转换开关的选型设计进行了分析,文献[12]提出了检验直流转换开关的2 种试验方法,文献[13-14]讨论了直流转换开关电路中避雷器的研制。由于两端直流输电系统的回线转换不涉及站间协调控制问题,因此以上研究结果并不适用于三端直流输电系统。
针对三端直流输电系统大地、金属回线转换策略的研究相对较少,文献[15]采用随机数原理对三端直流输电系统大地、金属回线转换过程中转换开关分断电流进行定量分析,但未考虑开关配置站点的影响,且对应数学模型的自变量较多,直接采用随机数模拟精度有限。因此,如何在考虑开关配置站点影响的前提下,简化转换开关电流应力求解过程并提高计算精度,选出适用于三端直流输电系统的最优大地、金属回线转换策略,是亟待解决的问题。
本文统筹考虑了转换开关配置站点以及转换策略对三端直流输电系统转换开关电流应力的影响,通过将偏微分与随机数原理相结合,逐次降低了数学模型中自变量的数目并极大弱化了对随机数模拟精度的需求,可有效评估不同转换开关配置站点以及不同转换策略对应的转换开关选型差异,优选后可以在不影响基本功能的前提下,使三端直流输电系统转换开关的开断容量最小从而直接减少工程投资,进而明确大地、金属回线转换的最优策略。同时,针对转换策略固定后可能引入的控制系统误判转移支路未建立,导致回线转换中断的问题,采取施加电流阶跃的措施,保证回线转换顺利执行。
1 三端直流输电系统大地、金属回线转换模型
1.1 模型建立
以图1 所示并联三端直流输电系统为例,建立图2 所示的大地、金属回线转换模型,从左到右依次定义3 个换流站分别为站1—3,稳态运行时,可将任意2站视为电流源,不妨定义容量较小的2站为电流源,如站2、3,其输出的直流电流分别为I2、I3,同时定义2 条直流线路的电阻分别为R1、R2,定义接地极1—3 的接地电阻分别为R3—R5。正极通过大地回线运行时,负极回路在图2中以虚线表示。
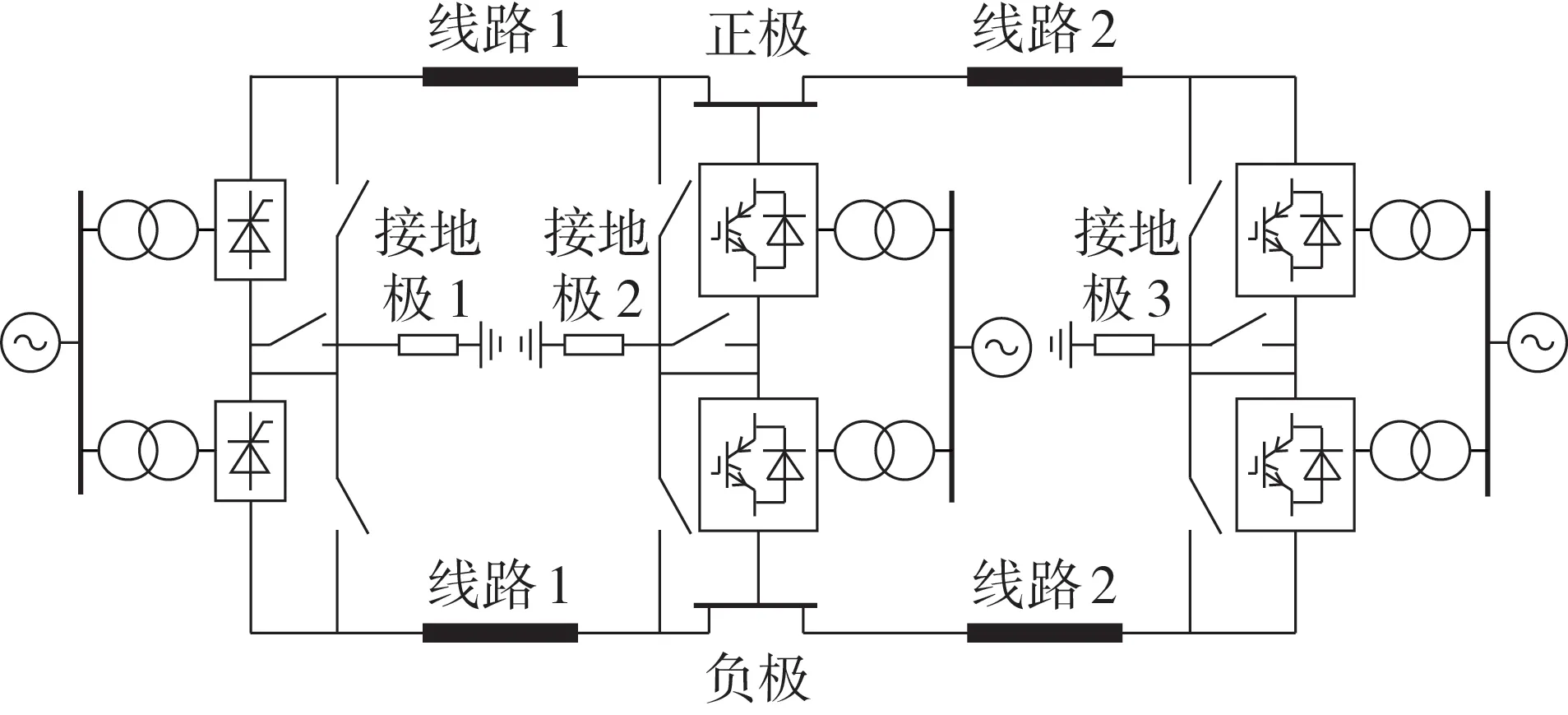
图1 并联三端直流输电系统拓扑Fig.1 Topology of parallel three-terminal DC transmission system
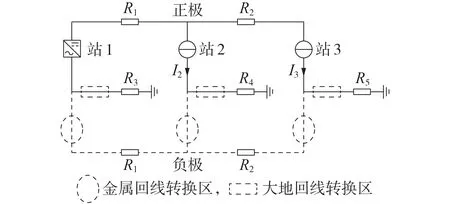
图2 三端直流输电系统正极大地回线运行示意图Fig.2 Schematic diagram of ground return operation of positive pole of three-terminal DC transmission system
如图2所示,三端直流输电系统各站均包含1个金属回线转换区和1 个大地回线转换区,用以实现大地、金属回线的转换。转换区需配置相应的转换开关,即金属回线转换开关MRTB(Metallic Return Transfer Break)或大地回线转换开关GRTB(Ground Return Transfer Break)。考虑到经济性,工程上不会在每个转换区均配置转换开关,以两端直流输电系统为例,只需在任意一站配置转换开关,另一站以转换刀闸配合即可完成转换,同时站点的选取不会对转换开关的开断容量产生影响,即不影响开关造价。对于三端直流输电系统而言,需在其中2 站配置转换开关,由于3 站的位置分布及容量并不对称,开关的配置站点及转换过程的分合顺序均会影响开断容量的选择,在工程设计阶段需要综合考虑。
其中开关位置设计如下:站1和站2配置转换开关为方案1;站1 和站3 配置转换开关为方案2;站2和站3 配置转换开关为方案3。同时每个方案可对应4种转换策略,以附录A图A1所示方案1下三端直流输电系统正极大地回线运行状态为例,进行金属回线转换时4 种转换策略定义如下:策略1,先将3 站的金属回线转移支路完整建立再先分左站GRTB1;策略2,先将3站的金属回线转移支路完整建立再先分右站GRTB2;策略3,先建立左站(站1)金属回线转移支路再分GRTB1;策略4,先建立右站(站2)金属回线转移支路再分GRTB2。
三端直流输电系统进行金属回线转换时,2 站中的MRTB 先后需分断的电流可用式(1)、(2)所示矩阵B1、B2表示。

式中:f(ij)、g(ij)(i=1,2,3;j=1,2,…,4)分别为方案i、策略j下B1、B2的7元(I2,I3,R1—R5)函数,构成矩阵内各元素,各元素的详细表达式见附录A 式(A1)—(A12)。上述矩阵对于任意呈放射式并联结构的三端直流输电系统均适用。
对于实际工程而言,各个站点的电流输出能力有明确的限制,同时各线路电阻可通过线路参数及气象资料确定浮动范围,以某三端直流输电系统为例,相关参数的分布范围如表1所示。
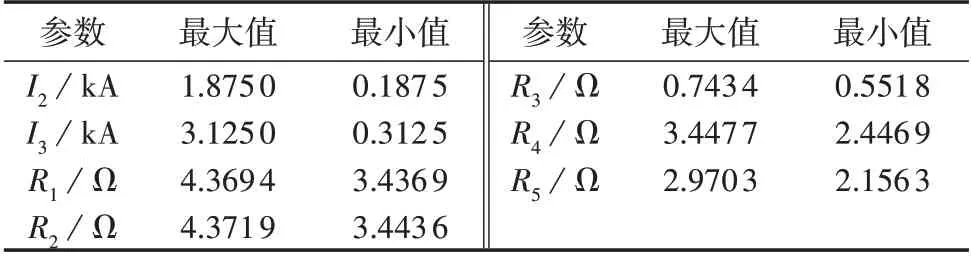
表1 某三端直流输电系统相关参数表Table 1 Some related parameters of three-terminal DC transmission system
以f(11)、g(11)为例,方案1策略1对应的MRTB开断能力要求如式(3)所示。
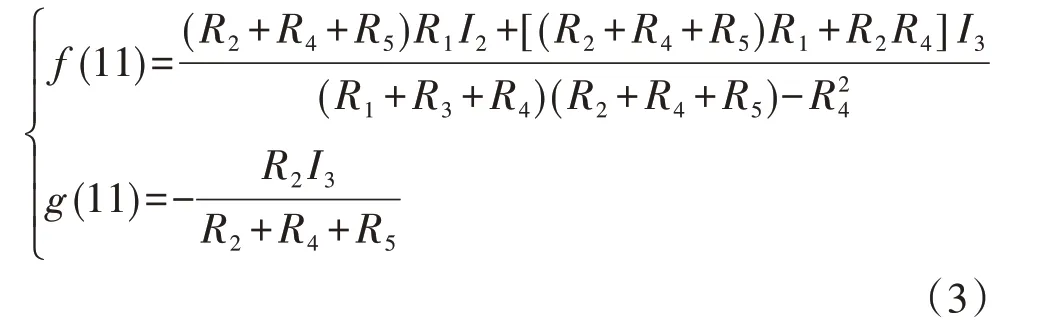
当进行设备选型时,应明确式(3)所示2 个元素的极大值,而对于7 元函数,极值的求解可能十分困难。文献[15]应用随机数原理求解极值,采用随机函数发生器,在仿真软件中产生各参数在其变化范围内的随机输出,并通过仿真获取每组随机取值下转换开关需分断的电流,将计算结果的最大值近似视作极大值。由于自变量较多,应用随机数求解的精度有限,即使随机计算107次,各自变量也仅能平均分布10个采样点,很难准确界定函数值域。
1.2 求解办法
针对直接采用随机数计算极值精度有限的问题并考虑到各参数取值的特点,本节提出一种将偏微分与随机数原理相结合的三端直流输电系统转换开关应力极值求解方法。
根据表1,各参数(特别是线路电阻)的定义域较窄,组合域内包含驻点的概率较低,换言之,矩阵B1、B2中各元素对7 个变量的偏微分在其取值范围内大概率为恒正或恒负,以f(11)为例,易知其对I2、I3的偏微分均大于0。基于此,提出了图3 所示开关应力极值求解逻辑,为便于软件实现,采用状态变量(x1—x7)描述函数中的7 个变量(I2,I3,R1—R5),其中xn(n=1,2,…,7)的最大值xnmax和最小值xnmin与对应参数的变化范围保持一致。
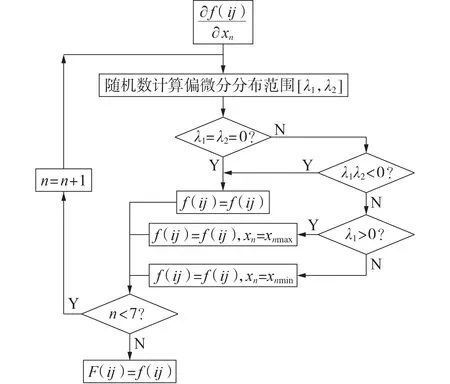
图3 开关应力极值求解逻辑Fig.3 Solution logic of extreme value of switching stress
图3 中F(ij)为f(ij)的极大值,在特殊情况下F(ij)仍包含自变量,此时采用随机数确定原函数值域的方案进行处理;λ1、λ2为偏微分分布范围的极限值。虽然图3 所示的求解过程同样采用了随机数原理,但与直接通过随机数确定原函数值域的方案呈现出明显区别。首先,循环求偏微分可逐次降低函数中自变量个数,其次,随机数计算仅用于确定偏微分的大致分布范围,相较于求解7 元函数的值域,对随机计算的精度和数量要求会大幅降低。例如,2次随机计算的结果为一正一负,即可明确偏微分的值域跨过原点,如果多次随机计算的输出均为正或均为负,则可大概率明确偏微分恒正或恒负。假设每个自变量取10 个采样点,本文所提求解方法与文献[15]所用方法的对比见表2。

表2 求解方法对比Table 2 Comparison of solution methods
g(ij)极大值G(ij)的求解逻辑与图3 一致,软件计算后可对应地形成矩阵B3、B4,见式(4)、(5)。


基于式(6)所示原则,利用MATLAB 软件遍历取小,即可明确MRTB 的最优配置站点及对应的金属回线转换策略。
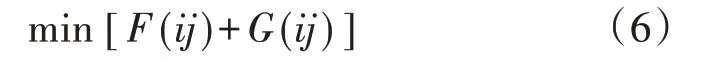
理论上,针对金属回线转大地回线工况,可以沿用上述逻辑确定GRTB 的最优配置站点及转换策略,但从管理及运维角度出发,MRTB 和GRTB 通常同时配置,而且由于远距离输电线路的电阻要大于接地极电阻,大地回线的分流作用更明显,MRTB 的容量需求更大,因此可认为MRTB 的优先级更高,MRTB 明确配置站点后,GRTB 的配置站点随之确定,仅需对转换策略进行择优。进行方案1下站1和站2配置大地回线转换时4种转换策略定义如下:策略1,先将3站的大地回线转移支路完整建立再分左站MRTB1;策略2,先将3 站的大地回线转移支路完整建立再分右站MRTB2;策略3,先建立左站(站1)大地回线转移支路再分MRTB1;策略4,先建立右站(站2)大地回线转移支路再分MRTB2。根据图3 依次求得4 种策略的极大值,利用MATLAB 软件遍历取小后即可明确最优的大地回线的转换策略,限于篇幅,此处不再赘述。
2 大地、金属回线转换开关应力极值求解
以表1 所示三端直流输电系统相关参数为例,应用MATLAB进行计算,计算结果见式(7)—(9)。

由式(7)—(9)知,MRTB 最优配置方案为方案3,即最优配置站点为站2和站3,最优金属回线转换策略为策略3,即先建立左站(站2)大地回线转移支路再分GRTB2。GRTB 配置站点随MRTB 确定,即选择方案3,4 种策略下2 个GRTB 先后需分断的电流可用矩阵D1、D2概括,详细表达式见附录B 式(B1)—(B6),计算极大值后形成的矩阵D3、D4见式(10)、(11),计算结果见式(10)—(12)。

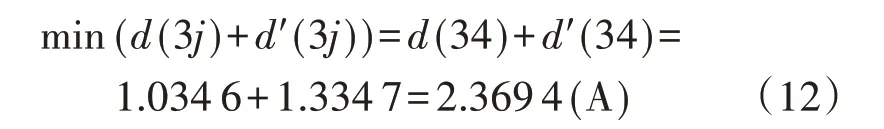
式中:d(3j)、d′(3j)分别为方案3 策略j下2 个GRTB先、后需要分断的电流峰值。由式(10)—(12)可知,最优大地回线转换策略为策略4,即先建立右站(站3)大地回线转移支路再分MRTB3。
3 大地、金属回线转换失败问题与应对措施
基于上述求解与优选,可明确三端直流输电系统转换开关的最优站点配置方案及对应的转换策略。然而在转换策略执行过程中,存在合MRTB(GRTB)后对应转移支路电流为0 的可能性,此时控制保护逻辑无法识别转移支路是否有效建立(有效建立判据为转换开关为合位且转移支路电流大于门槛值);与此同时,为了避免操作过电压造成设备损坏,现有控制保护逻辑均包含转移支路未有效建立,联锁逻辑禁止释放本站GRTB(MRTB)分闸信号,进而导致转换失败。为了克服大地、金属回线转换策略存在的转换失败问题,提高转换策略的可靠性,本文提出了应对措施。
3.1 问题分析
根据表1 对应的三端直流输电系统相关参数以及第2节的计算结果,其最优开关配置站点为站2和站3,大地回线转金属回线时应先建立左站(站2)大地回线转移支路再分GRTB2,金属回线转大地回线时应先建立右站(站3)大地回线转移支路再分MRTB3。设流经转换开关与刀闸(Q5、Q71)的电流定义分别为IMRTB2、IGRTB2、IMRTB3、IGRTB3与IQ5、IQ71。按该顺序执行大地回线至金属回线的转换,站2 完成转换且合上GRTB3后,其接线方式如图4所示。
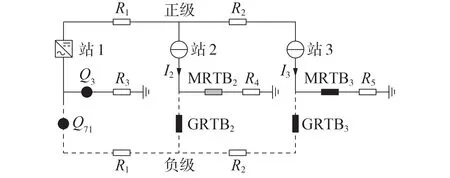
图4 大地回线转金属回线中间过程示意图Fig.4 Schematic diagram of intermediate process from ground return to metallic return
图4 中流经GRTB3的电流,可视作由等效电流源I2在GRTB3上产生的电流激励IGRTB3_I2与等效电流源I3在GRTB3上产生的电流激励IGRTB3_I3叠加产生,其电路模型如图5所示。
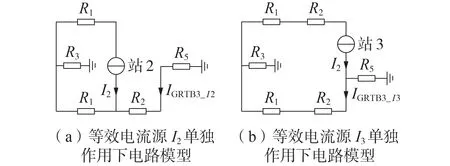
图5 大地回线转金属回线中间过程等效电流源模型Fig.5 Equivalent current source model in intermediate process from ground return to metallic return
GRTB3上流过的电流表达式如式(13)所示。
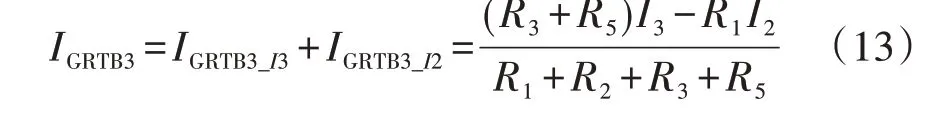
同理,金属回线转大地回线过程中,站3 完成转换且合上MRTB2后,其接线方式见附录C 图C1。图C1 中流经MRTB2的电流由等效电流源I2在MRTB2上产生的电流激励IMRTB2_I2及等效电流源I3在MRTB2上产生的电流激励IMRTB2_I3叠加产生,如附录C 图C2所示。MRTB2上流过的电流表达式见式(14)。

由式(13)、(14)可知,2 个等效电流源在GRTB3(MRTB2)上产生的电流激励方向相反,且范围存在交叉,在特定的线路电阻或电流比例下可相互抵消,此时控制保护装置无法识别站3金属转移支路(站2大地转移支路)是否有效建立,联锁逻辑禁止释放MRTB3(GRTB2)分闸信号,造成转换失败。
3.2 解决措施
转移支路电流与站2和站3电流直接相关,因此转移电流过小不满足有效建立判据时,可采用调整各站电流水平的方式,主动使转移支路流过较大电流,避免因联锁逻辑禁止释放MRTB3(GRTB2)分闸信号,造成转换失败。结合表1 所示参数分布范围,对式(13)、(14)求偏微分后易知,IGRTB3_I2、IMRTB2_I2的边界斜率绝对值大于IGRTB3_I3、IMRTB2_I3,即调整站2 直流电流对改变转移支路电流的效果更显著,应优先调整站2功率。
该三端直流转移支路有效建立的电流门槛值为20 A,计及10 A 的测量误差,大地回线转金属回线过程中,站2 电流调整值按式(15)确定,其中0.302为IGRTB3_I2随I2变化曲线的斜率最小值。
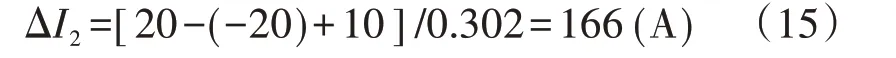
同理,金属回线转大地回线过程中,站2 直流电流调整值如式(16)所示,其中0.466 为IMRTB2_I2随I2变化曲线的斜率最小值。
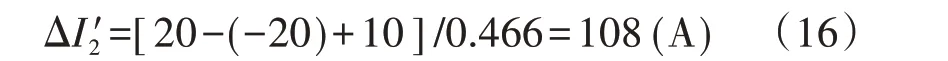
4 大地、金属回线转换失败应对措施仿真
根据表1所示三端直流输电系统参数,在PSCAD中搭建仿真模型。由于式(15)、(16)已充分考虑裕度,仿真中设大地、金属回线转换策略下站2 的直流电流调整值均为160 A。当(I2,I3,R1,R2,R3,R4,R5)=(1.5 kA,2 kA,4 Ω,4.3719 Ω,0.6 Ω,3.4477 Ω,2.4 Ω)时,大地回线转金属回线过程中,流经转换开关与刀闸的电流波形如图6 所示,图中,t1—t7分别表示进行合Q71、合GRTB2、分MRTB2、合GRTB3、I2向下阶跃、分MRTB3、分Q5操作的时刻,SMRTB3为MRTB3的分合状态,其取值为1表示合闸,取值为0表示分闸。
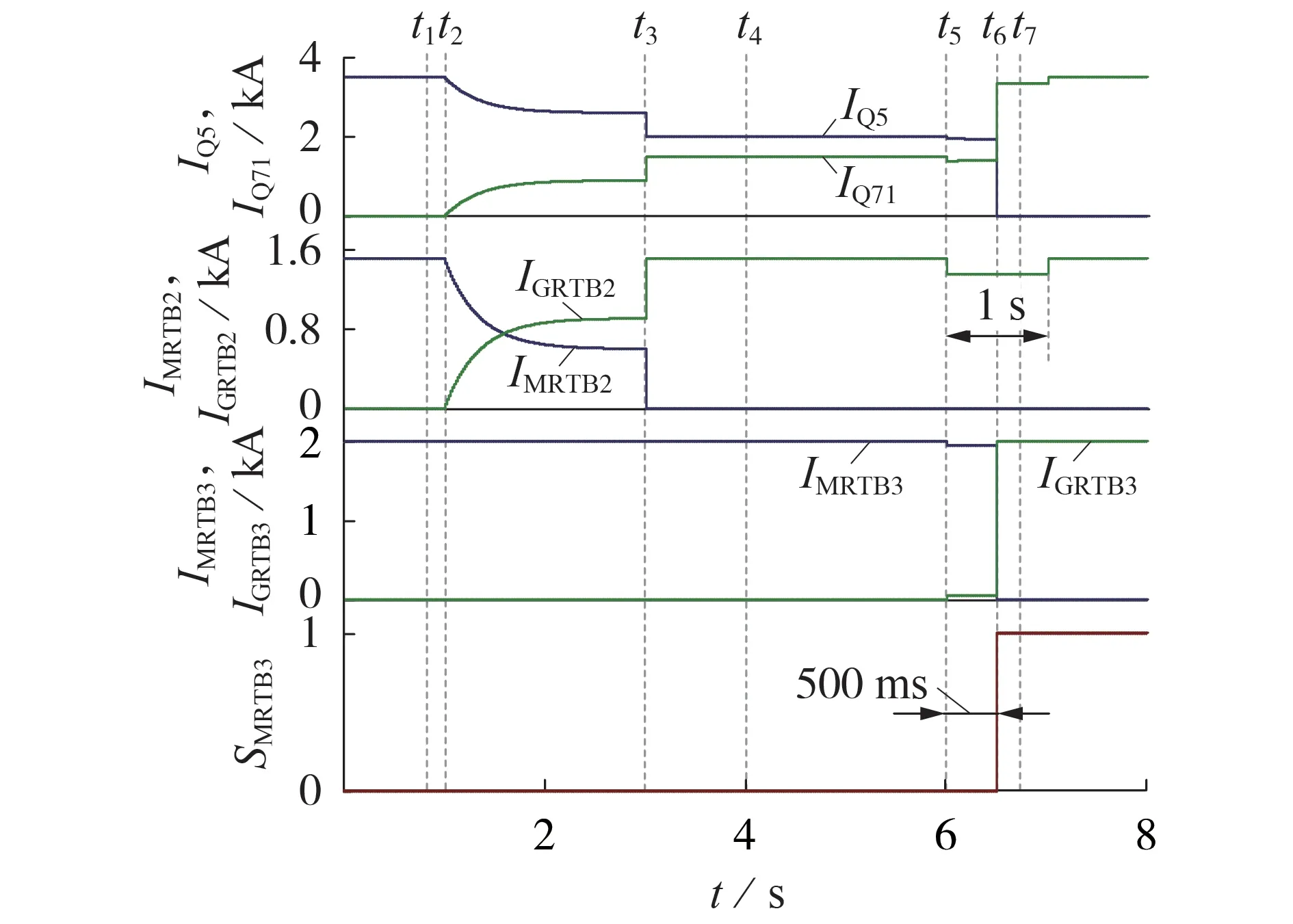
图6 大地回线转金属回线过程中3站直流电流Fig.6 DC current of three stations in process from ground return to metallic return
由图6 可知,4 s 时GRTB3合闸后,站3 金属转移支路上电流为0,不满足转移支路有效建立判据,禁止释放MRTB3分闸信号。为了顺利执行后续转换操作,6 s 时站1、站2 直流电流向下阶跃160 A 并持续1 s,站3金属转移支路上电流上升至56 A,经500 ms延时后释放MRTB3合闸信号,完成回线转换。
当(I2,I3,R1,R2,R3,R4,R5)=(0.5 kA,2.5 kA,3.5 Ω,4.371 9 Ω,0.7 Ω,3.447 7 Ω,2.970 3 Ω)时,金属回线转大地回线过程中,流经转换开关与刀闸的电流如图7所示,图中,t′1—t′7分别表示进行合Q5、合MRTB3、分GRTB3、合MRTB2、I2向上阶跃、分GRTB2、分Q71操作的时刻,SGRTB2为GRTB2的分合状态,其取值为1 表示GRTB2合闸,取值为0表示GRTB2分闸。
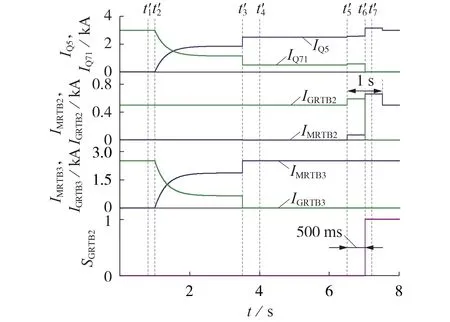
图7 金属回线转大地回线过程中3站直流电流Fig.7 DC current of three stations in process from metallic return to ground return
由图7 可知,4 s 时MRTB2合闸后,站2 大地转移支路上电流为0,不满足转移支路有效建立判据,禁止释放GRTB2分闸信号。为顺利执行后续转换操作,6.5 s时站1、站2直流电流向上阶跃160 A并持续1 s,站2大地转移支路上电流上升至72 A,经500 ms延时后释放GRTB2分闸信号,完成回线转换。
5 结论
本文提出采用偏微分与随机数原理相结合的方法,准确评估不同方案、转换策略下转换开关电流应力的极大值,明确三端直流输电系统大地、金属回线转换开关的最优配置站点与转换策略。与此同时,本文分析了采用最优转换策略可能引入的回线转换失败问题,并提出通过改变各站电流水平,在首次转换中断后主动使转移支路流过较大电流的应对措施。本文所提优选方法与应对措施,对后续三端直流输电系统转换开关的配置、回线转换策略的选择及相关控制逻辑的完善具有较强的借鉴意义。
附录见本刊网络版(http://www.epae.cn)。

