基于多源气象预报总辐照度修正的光伏功率短期预测

师浩琪，郭 力，刘一欣，王成山

（天津大学 智能电网教育部重点实验室，天津 300072）

0 引言

近年来，为了缓解能源危机，以光伏发电为代表的可再生能源发展迅速，但其出力的不确定性和波动性给电网的安全稳定运行带来了巨大冲击［1］。因此，准确预测光伏功率对电网制定更加精细的调度计划、提高电力系统可靠性有重要的现实意义［2］。

目前已有很多学者围绕光伏电站日前24 h短期预测开展研究。在数据预处理方面，对预测模型的训练数据划分不同天气类型有助于建立更加精细的预测模型［3］，但在天气类型划分方面，目前还没有统一的标准。文献［4］根据温度、湿度、辐照度的特征，采用改进Kohonen 神经网络进行天气聚类。文献［5］根据云量、辐照度、温度采用概率神经网络PNN（Probabilistic Neural Network）算法划分天气类型。上述历史数据分类模型未考虑各气象因素之间的相关关系，深层特征挖掘不足，存在数据冗余现象。在预测方法方面，随着大数据技术的发展，人工智能算法相较于统计方法和物理方法应用更加广泛［6］，主要包括人工神经网络［7-8］、支持向量机［9］以及多模型组合算法［10］等。文献［7］以温度、湿度等气象数据和相似日功率数据为输入变量，采用反向传播BP（Back Propagation）神经网络预测光伏功率。文献［8］额外引入天气类型指数作为BP 神经网络预测模型的输入变量，预测不同天气类型下的光伏功率。文献［9］采用变分模态分解VMD（Variational Mode Decomposition）将历史光伏发电功率分解成多个子模态，用最小二乘支持向量机LSSVM（Least Square Support Vector Machine）分别预测光伏发电功率和误差。文献［10］针对各天气分型下的波动过程和类晴空过程，建立卷积神经网络CNN（Convolutional Neural Network）和长短期记忆LSTM（Long Short Term Memory）网络的组合预测模型。在预测数据源选择方面，短期预测算法多以数值天气预报NWP（Numerical Weather Prediction）为气象数值预报源［11-12］，以公共气象服务预报为天气状态预报源［13］。文献［11］对高维NWP 数据进行降维处理，在筛选相似日样本的基础上，通过LSTM 网络预测模型建立气象因素与光伏功率之间的映射关系。文献［12］以数据采集与监视控制SCADA（Supervisory Control And Data Acquisition）系统的功率数据和NWP 数据建立小波-粒子群-支持向量机预测模型。上述文献以NWP 原始数据为输入，建立NWP-功率映射模型，但由于NWP 存在误差，该模型不能准确描述气象-功率之间的关系。另外，由于NWP 误差的不确定性，NWP-功率映射模型不能有效消除NWP 误差对功率预测的影响。文献［13］对所划分的广义天气类型分别建立预测模型，并根据公共气象服务预报的预测日天气类型选择预测模型进行预测。由于公共气象服务预报的区域范围较大，与光伏发电预测要求的精细化气象预报场景存在较大差异，故须对公共气象服务预报的准确度进行评估。针对NWP预报偏差较大的问题，很多学者一直尝试解决，如采用模式后处理［14-15］等方法进行修正，但效果不明显。利用数据融合和数据同化技术综合多种来源的观测资料或者模拟数据，可获得高精度、高质量的多源数据融合气象预报产品［16］。然而目前应用于光伏功率预测领域的气象数据融合研究还比较少。

针对上述问题，本文提出基于多源气象预报总辐照度修正的光伏功率短期预测方法。首先，根据功率序列特征采用自组织映射SOM（Self Organizing Map）神经网络聚类算法划分广义天气类型，并与公共气象服务天气类型预报实现匹配对应，分类方法具有较高的准确度和较强的适应性；然后，通过融合预测日NWP 和公共气象服务天气类型预报，基于树扩展朴素贝叶斯TAN（Tree Augmented Naive Bayes）算法评估2种气象预报源的准确度，再结合实测总辐照度数据实现预测日NWP 总辐照度修正；最后，以实测气象和功率为训练样本，得到准确反映气象与功率映射关系的预测模型，并以修正后的总辐照度为输入实现光伏功率短期预测。利用我国某光伏电站的实际运行数据和气象预报数据验证了模型的有效性。

1 基于总辐照度修正的光伏功率预测

光伏输出功率受多种外部气象因素和自身组件状态的影响，为构建高效、精确的预测模型，本节首先分析光伏发电影响因素，并筛选预测模型输入变量，然后介绍本文提出的基于多源气象预报总辐照度修正的光伏功率短期预测模型框架。

1.1 影响因素分析

光伏功率主要受两方面因素影响［17］：一方面是光伏电站所处位置的辐照度、温度等气象因素；另一方面是光伏面板倾角、组件转换效率等自身因素。在不发生故障的情况下，光伏组件自身因素在短期内变化较小，研究预测问题时可以忽略其对光伏功率的影响。

不同天气类型下光伏电站功率曲线特征具有明显差异。按照中国天气网对天气状态的预报形式，结合光伏电站所在地区的气候特点，以我国河南省某光伏电站为例，分析该地区天气类型占比较大的晴天（41.00%）、多云天（27.83%）、阴天（13.64%）和雨雪天（16.08%）4 种典型天气类型下光伏电站功率曲线特征，功率曲线如图1所示。

由图1 可知：晴天和多云天功率幅值较大，但晴天功率曲线较为平滑，多云天由于云层移动的影响其功率曲线呈现较强的波动性；阴天和雨雪天功率幅值较小并呈现出一定的波动性。通常而言，对于气象要素变化平缓的天气类型（如晴天），光伏预测精度较高，对于气象要素波动性强、变化规律不明显的天气类型（如多云天、阴天和雨雪天），由于气象要素预测的难度较大、精度较低，光伏功率预测偏差较大，因此有必要通过划分天气类型，采取针对性的预报方法或者修正方法来提高光伏功率预测精度。

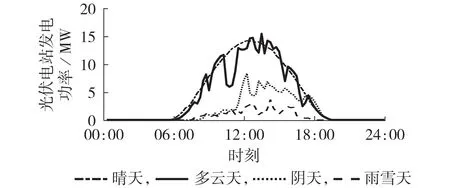
图1 不同天气类型下光伏电站功率曲线Fig.1 Power curves of photovoltaic power plant under different weather types

到达地面的太阳辐射包括直射辐射和散射辐射，两者之和称为总辐射。直射辐射是指没有被任何物质所散射，直接到达地面的太阳辐射；散射辐射则是太阳辐射经过大气和云的散射后到达地面的太阳辐射。单位面积辐射量称为辐照度。总辐照度是光伏功率的直接影响因素，而气温、湿度、风速、气压等其他因素通过影响总辐照度的强弱间接影响光伏功率。随机选取连续3 d 采样时间间隔为15 min 的实测数据，采用皮尔森相似度分析法计算气象因素与光伏功率之间的相关性，不同气象因素与光伏功率间的皮尔森相关系数见表1。

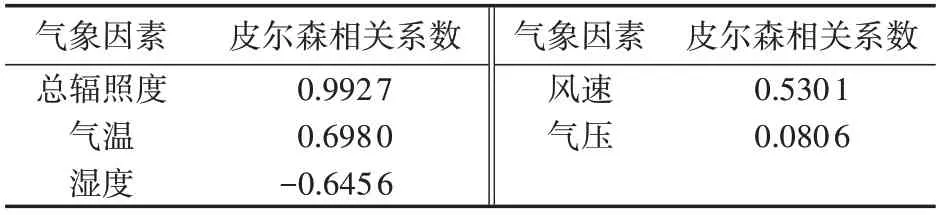
表1 气象因素与光伏功率间的皮尔森相关系数Table 1 Pearson relevant coefficient between meteorological factors and photovoltaic power

由表1 可知：总辐照度与光伏功率呈现极强的正相关性；实际中，虽然气温升高导致光伏组件效率降低，但在该过程中往往天气越晴朗，太阳辐射越强，从而使光伏功率增大，综合效果来看，气温和光伏功率呈现较强的正相关性；湿度和风速也与光伏功率呈现出较强的相关性。因此本文以上述4 种因素作为光伏功率预测模型的输入变量，并对最关键的总辐照度因素进行修正，以提高功率预测精度。

1.2 预测模型框架

单一气象预报源存在误报和偏差的问题，综合多种气象预报源可提升气象预报产品的精度，本文使用的多源气象预报包括2 种气象源：一种是预测日的NWP 数据，通常由NWP 服务机构提供；另一种是预测日公共气象服务天气类型预报，通常来源于中央气象台、中国天气网等天气类型预报服务机构。在获取这2 种信息的基础上，本文所提基于多源气象预报总辐照度修正的光伏功率短期预测模型框架见图2，主要包括光伏电站历史数据分类、NWP 广义天气类型分类、广义天气类型转移概率计算、NWP总辐照度修正和遗传算法GA（Genetic Algorithm）优化的BP（GA-BP）神经网络预测5个部分。目前关于GA-BP神经网络算法的研究较成熟，本文不再赘述。

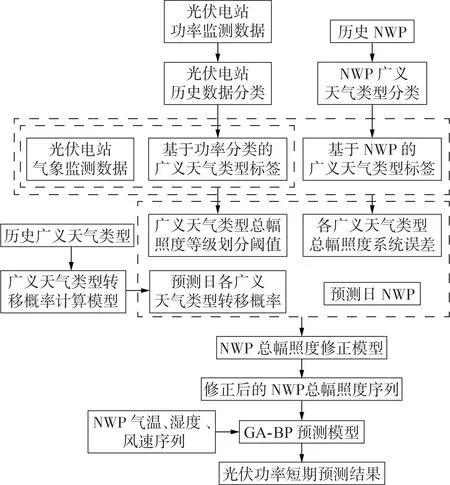
图2 光伏功率短期预测模型框架Fig.2 Framework of short-term photovoltaic power forecasting model

2 光伏电站历史数据分类

本节以光伏日功率序列为研究对象，提取光伏日功率序列特征，采用SOM 神经网络聚类算法进行光伏电站历史数据广义天气类型划分，并对各广义天气类型的总辐照度划分不同等级。光伏电站历史数据分类模型框架见附录A图A1。

2.1 基于SOM 神经网络聚类算法的光伏电站历史数据分类

光伏功率与多种气象因素密切相关，因此光伏功率可反映多种气象因素的综合变化。以光伏日功率序列特征构建特征向量进行聚类分析，综合了各气象要素场的关联关系，分类结果有较高的准确度。

2.1.1 光伏日功率序列特征

如图1 所示，不同天气类型下光伏功率序列呈现出不同的幅值和波动情况，因此光伏日功率序列的幅值和波动特征反映了该日天气状态。本文对每日白昼时段的光伏日功率序列进行小波变换［18］，分解层数为4，得到反映光伏功率变化趋势的近似信号A4和反映光伏功率随机波动的细节信号D1—D4，将近似信号A4作为该日晴空序列u，细节信号D1—D4之和作为该日波动序列v，基于晴空序列u和波动序列v构建的光伏日功率序列特征如下。

1）幅值特征。

以晴空序列u的平均值uˉ衡量光伏功率幅值大小，如式（1）所示。

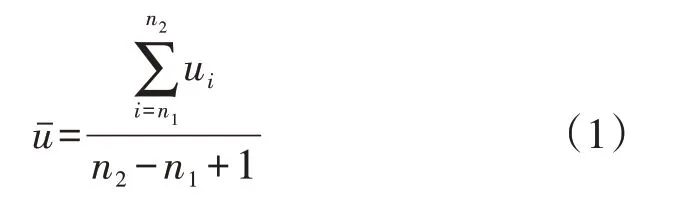
式中：ui为晴空序列u中第i个采样点的功率值；n1和n2分别为采样起始位置和结束位置。

2）波动特征。

（1）波动幅值特征。

以波动序列v的一阶差分指标Δf衡量光伏功率波动幅值，如式（2）所示。

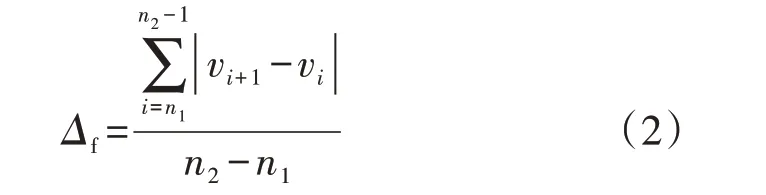
式中：vi为波动序列v中第i个采样点的功率值。

（2）波动频率特征。

将波动序列v进行快速傅里叶变换，确定其中心频率，以中心频率衡量光伏功率波动快慢。

2.1.2 SOM神经网络聚类

SOM神经网络根据人脑神经系统中兴奋和抑制的现象，采用“竞争学习”的方式，实现对不同特征样本的分类，其结构和算法步骤见附录B。

SOM 神经网络聚类算法根据数据间的相似性，通过自组织、自适应改变网络的权值，可消除输入噪声的影响，但其聚类数需事先设定。本文借鉴层次聚类的思想，自顶向下利用SOM 神经网络聚类算法，以2.1.1 节中的光伏日功率序列特征为输入变量，采用逐步二分的方式将光伏电站历史数据划分为N类广义天气类型，分类过程见附录A图A2，然后如附录A图A3所示按晴朗程度实现广义天气类型与同时间范围内公共气象服务天气类型预报匹配对应。

2.2 实测总辐照度等级划分与折算

风速越大，对大气中云团和悬浮物的推动作用越大，天气越晴朗，总辐照度越大；湿度越大，大气中的水汽对总辐照度的阻挡作用越大。特定的广义天气类型对应多种公共气象服务天气类型预报，不同公共气象服务天气类型预报如阴、雾、扬沙、霾的总辐照度大小不同，因此，各广义天气类型下由于其他气象因素的影响或包含更精细的天气类型，总辐照度呈现出不同水平。为构建更精细的总辐照度修正模型，需对各广义天气类型的总辐照度等级进行划分，广义天气类型c总辐照度等级划分流程如下。

1）根据2.1 节中的光伏电站历史功率数据广义天气类型划分结果，绘制广义天气类型c总辐照度散点图。

2）计算广义天气类型c各时刻总辐照度序列不同分位数值，构建分位数值时间序列。广义天气 类 型c第i个 采 样 点 的 总 辐 照 度 序 列Rc，i=[Rc，1，i，Rc，2，i，…，Rc，Kc，i]，其 中Rc，j，i(j=1，2，…，Kc)为 广 义 天气类型c第j个样本中第i个采样点的总辐照度值，Kc为广义天气类型c所包含的样本数。若Rc，i的α分位数值R′c，i，α满足P(Rc，j，i≤R′c，i，α)=α，则广义天气类型c的α分位数值时间序列R′c，α=[R′c，1，α，R′c，2，α，…，R′c，h，α]，其中P(A)表示事件A成立的概率，h为采样点数。

3）利用高斯滤波法对广义天气类型c总辐照度分位数值时间序列进行平滑处理。

4）定义广义天气类型c相邻分位数值时间序列之间的总辐照度散点带，将其按照从高到低分别分为等级1—M。

将各广义天气类型总辐照度均按上述方法划分为多个等级后，将上下界分位数值时间序列的平均值作为该等级的代表序列。根据不同广义天气类型同一等级的代表序列计算不同广义天气类型间的总辐照度折算系数序列。广义天气类型c1和c2间总辐照度等级i的折算系数序列λc1→c2，i按式（3）进行计算。

3 基于TAN的广义天气类型转移概率计算

天气状态变化具有连续性，本文天气类型转移概率定义为在预测日前几日天气类型一定的情况下，预测日各天气类型发生的概率。某日邻近前几日的天气状态与该日天气状态具有相关性，不满足传统朴素贝叶斯算法各属性变量之间相互独立的假设。本文使用TAN 算法计算预测日各广义天气类型的转移概率，该算法在朴素贝叶斯算法的基础上，假设每个条件属性在类别属性之外最多依赖于1 个其他条件属性。根据该思想，本文将预测日的广义天气类型作为类别属性，将预测日前D天的广义天气类型作为条件属性，计算预测日各广义天气类型的转移概率，以此评估各气象预报源的准确性。广义天气类型转移概率计算模型框架见附录A 图A4。TAN算法步骤见附录C。

广义天气类型转移概率的大小对总辐照度修正值的精度有很大影响，为确定转移概率计算模型的最适条件属性数，本文提出转移概率有效率Ie来评估转移概率的有效性，计算公式为：

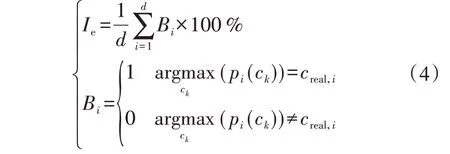
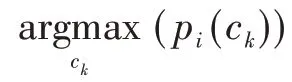
4 基于NWP 广义天气类型分类的总辐照度修正

以反映云量多少的日均直总辐照度比作为NWP 广义天气类型分类的标准，通过分析NWP 广义天气类型分类正确的样本计算NWP 总辐照度系统误差，引入公共气象服务天气类型预报源，并结合广义天气类型转移概率修正NWP 总辐照度。NWP总辐照度修正模型框架见附录A图A5。

4.1 NWP广义天气类型分类

有关研究结果表明，在云量较少、大气透明度较高的时段，总辐照度中直射辐照度占比较大，因此直射辐照度和总辐照度的比值反映了云量的多少。根据2.1节中的各广义天气类型所占比例，对同一时间范围内NWP 日均直总辐照度比进行排序，按比例求取各广义天气类型日均直总辐照度比阈值，即可根据预测日NWP 数据确定预报的广义天气类型。日均直总辐照度比η按式（5）进行计算。

4.2 NWP总辐照度系统误差计算

NWP总辐照度系统误差计算步骤如下：

1）根据2.1 节中的历史功率数据分类模型确定样本集的广义天气类型；

2）根据4.1 节中的日均直总辐照度比确定样本集NWP广义天气类型；

3）从样本集筛选NWP 广义天气类型分类正确的样本，本文NWP 广义天气类型分类正确的样本定义为与NWP 广义天气类型与功率分类确定的广义天气类型相同的样本；

4）在NWP 广义天气类型分类正确的样本中分别计算各广义天气类型下NWP总辐照度系统误差。

4.3 NWP总辐照度修正

在预测日前一天从不同的气象服务机构获取预测日的NWP 数据和公共气象服务天气类型预报，判断预测日NWP 广义天气类型cNWP与公共气象服务预报的广义天气类型cWTF是否一致：若一致，则仅修正总辐照度系统误差即可得到用于功率预测的总辐照度序列，即广义天气类型cNWP的总辐照度序列RcNWP；若不一致，则根据辐照度较高时段11:00—13:00 的总辐照度平均值判断广义天气类型cNWP总辐照度等级i，根据广义天气类型cNWP和cWTF之间总辐照度等级i的折算系数序列λcNWP→cWTF，i得到广义天气类型cWTF的总辐照度序列RcWTF。由预测日广义天气类型转移概率模型分别计算NWP 广义天气类型cNWP和公共气象服务预报的广义天气类型cWTF的转移概率P(cNWP)和P(cWTF)，并以转移概率为权重对2种广义天气类型下的总辐照度序列进行求和，得到用于功率预测的总辐照度序列R*。NWP总辐照度2步修正示意图见附录A 图A6。用于功率预测的总辐照度序列R*按式（11）进行计算。

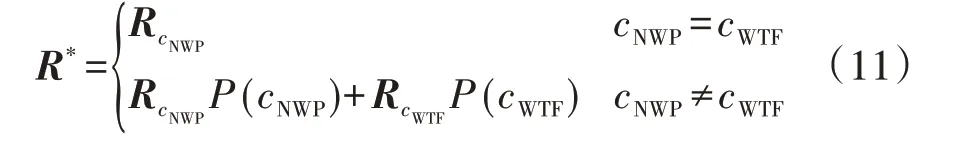
式（11）中公共气象服务预报的广义天气类型cWTF对应的总辐照度序列RcWTF按照式（12）进行计算。

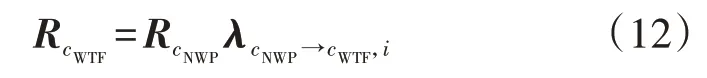
5 算例分析

以我国某装机容量为20 MW 的光伏电站2018年6 月1 日至2019 年5 月31 日的实测数据和相关气象预报数据为样本。NWP 数据来源于德国天气在线数值预报数据中心，该中心基于WRF（Weather Research and Forecasting）模式对全球预报系统GFS（Global Forecast System）背景场数据进行计算模拟；公共气象服务天气类型预报数据来源于中国天气网。以2018年6月1日至2019年4月30日的样本作为训练样本，2019 年5 月1 日至2019 年5 月31 日的样本作为测试样本，对本文所建立的光伏功率短期预测模型进行验证。根据测试样本所在季节的日出日落时间，选取06:30—18:30 时段的功率作为功率预测的对象。另外，根据2017—2019 年的公共气象服务天气类型预报数据建立和验证广义天气类型转移概率计算模型。

5.1 光伏电站历史数据分类

提取日功率序列特征并采用SOM 神经网络聚类算法进行逐步分类，由戴维森堡丁指数DBI［19］（Davies Bouldin Index）确定分类数N，DBI 越小，分类效果越好。不同分类数N对应的DBI变化见图3。

理论上，广义天气类型种类越多，分类模型越精细，但预测模型的复杂度越高。由图3可知，当N=4时，DBI 出现明显拐点，因此本文将历史数据划分为4 种广义天气类型。通过比较聚类中心发现：广义天气类型1和2的日功率幅值较大，但广义天气类型1的日功率波动性较小，广义天气类型2的日功率波动性较大；广义天气类型3和4的日功率都呈现出一定的波动性，但广义天气类型4的日功率幅值更低。

样本时间范围内光伏电站所在地区公共气象服务天气类型预报包括晴、多云、阴、小雨、中雨、大雨、暴雨、阵雨、雷阵雨、雾、霾、扬沙、小雪、大雪、雨夹雪共15 种天气类型。将这15 种天气类型按照晴朗度排序，并与本文划分的4 种广义天气类型进行匹配，匹配结果及各天气类型占比见表2。

由表2 可以看出，在一定误差范围内，公共气象服务天气类型预报与本文所划分的4 种广义天气类型具有较高的匹配度，验证了本文提出的基于功率特征的历史数据分类方法的有效性。

在总辐照度等级划分上，针对难以细化的广义天气类型1和2，由于风速、湿度等其他因素的影响，总辐照度呈现出不同的水平。针对包含多种精细天气状态的广义天气类型3和4，不同的精细天气状态对应不同的总辐照度水平，兼顾典型性和代表性，本文将各广义天气类型总辐照度划分为10%、30%、50%、70%、90%这5个分位数序列，共4个等级。各广义天气类型总辐照度等级及分位数界见表3。

此外，位于10%分位数序列以下和90%分位数序列之上的总辐照度序列出现的概率较低，分别将其归为等级4 和等级1。广义天气类型1 所有样本总辐照度散点图及等级划分如图4 所示。其他广义天气类型所有样本总辐照度散点图及等级划分见附录D 图D1—D3。图5 为广义天气类型3 总辐照度等级及其对应的精细天气状态示意图，图中阴、雾、扬沙、霾4 种天气类型分别对应总辐照度等级1—4。另外，经统计验证可知：广义天气类型4 中小雨、阵雨、雷阵雨天气下的辐照度水平较高，属于等级1；中雨、大雨天气下的辐照度水平属于等级2；暴雨、小雪天气下的辐照度水平属于等级3；大雪、雨夹雪天气下的辐照度水平属于等级4。

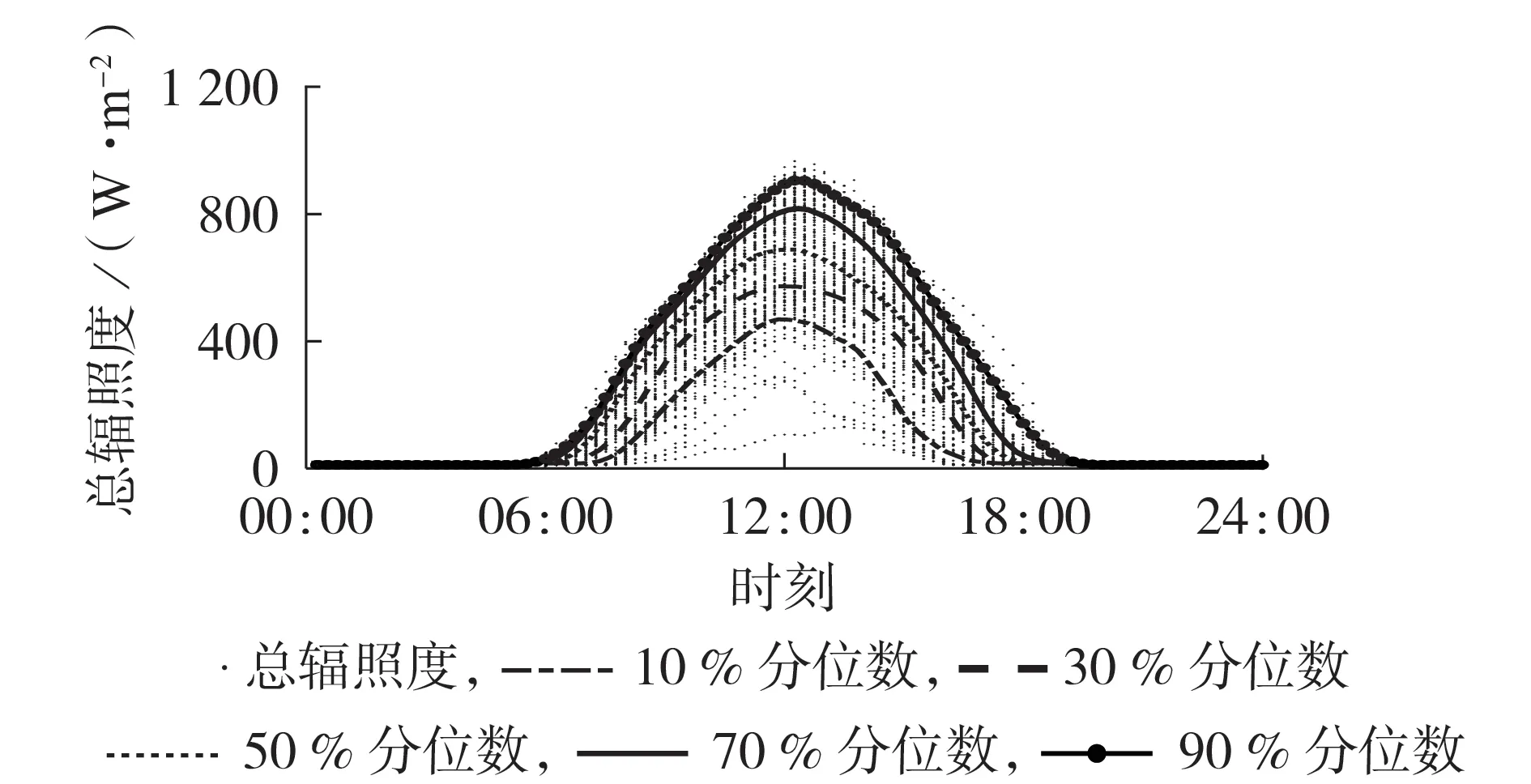
图4 广义天气类型1总辐照度散点图及等级划分Fig.4 Scatter diagram and classification of total irradiance for Generalized Weather Type 1

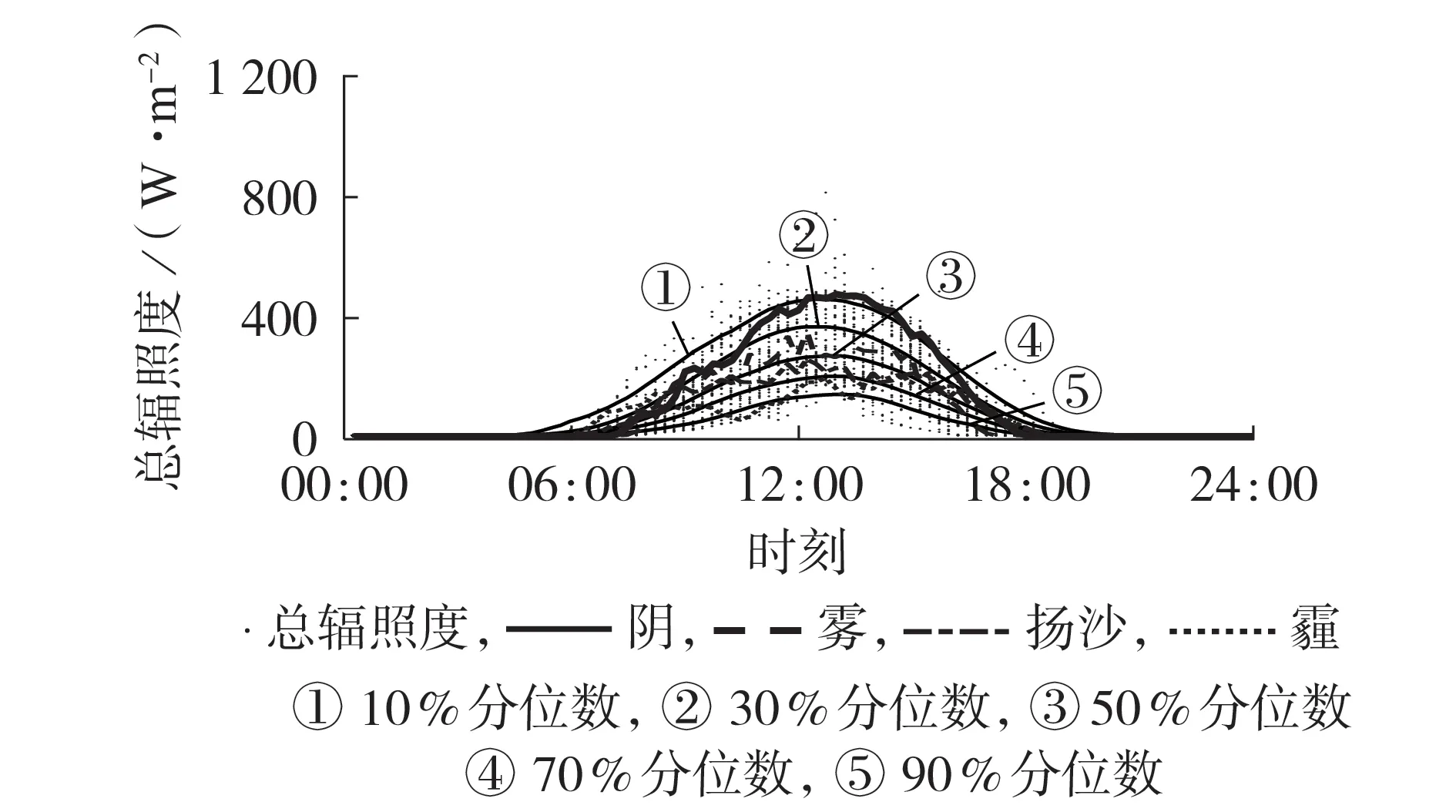
图5 广义天气类型3总辐照度等级及精细天气状态Fig.5 Total irradiance levels and fine weather condition for Generalized Weather Type 3

5.2 广义天气类型转移概率有效性评估

为确定基于TAN 的广义天气类型转移概率模型的最适条件属性数，考虑到与预测日间隔天数越多，天气状态间的相关性越弱，本文分别以预测日前1—6 d 作为预测日转移概率计算的属性变量，并通过转移概率有效率Ie评估不同属性变量数下的转移概率有效性。

由于光伏电站历史数据时间范围较小，不适用于建立和验证广义天气类型转移概率计算模型，且虽然较长时间范围内公共气象服务预报的广义天气类型存在一定误差，但当样本集足够大时，以公共气象服务预报结果建立的广义天气类型转移概率模型与以实际广义天气类型建立的转移概率模型趋于一致，因此本文以2017 年1 月1 日至2019 年4 月30 日公共气象服务预报的广义天气类型作为训练样本，2019 年5 月1 日 至2019 年12 月31 日 公 共 气 象 服 务预报的广义天气类型作为测试样本，分别建立不同属性变量数的转移概率计算模型，对应的转移概率有效率如表4所示。

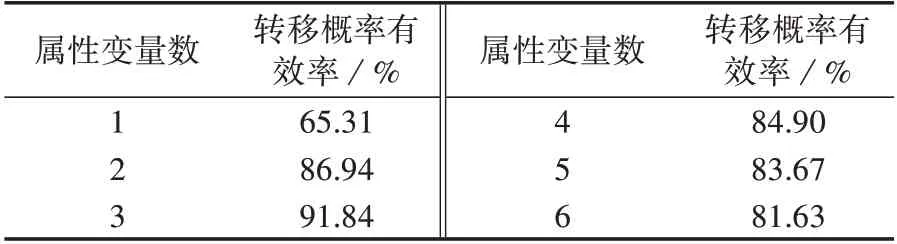
表4 不同属性变量数下的转移概率有效率Table 4 Transfer probability efficiency under different numbers of attribute variables

由表4 可知：仅用预测日前1 d 的广义天气类型作为属性变量计算预测日广义天气类型转移概率具有较大的偶然性，转移概率有效率较低；当用预测日前3 d的广义天气类型作为属性变量时，既保证了预测日前3 d 的广义天气类型与预测日广义天气类型具有较强的相关性，又避免了属性变量较少时转移概率偶然性较大造成转移概率有效率较低的问题；当属性变量继续增加时，距离预测日时间较长的属性变量的广义天气类型与预测日广义天气类型的相关性较小，对预测日广义天气类型的判定造成干扰，导致转移概率有效率降低。因此，本文选择预测日前3 d 的广义天气类型作为预测日广义天气类型转移概率计算的属性变量。

5.3 功率预测结果分析

本文将总辐照度、温度、湿度、风速作为GA-BP神经网络的输入变量，功率作为输出变量，使用五折交叉验证进行模型参数寻优，将训练样本平均划分为5 个互斥子集，其中4 个子集作为训练集，另外1个子集作为验证集，每组模型参数循环验证5 次，将5 次预测结果的平均误差作为最终误差，选取误差较小时的模型参数作为最终GA-BP 预测模型参数。模型参数见附录D表D1。

本文选取平均绝对误差MAE（Mean Absolute Error）和均方根误差RMSE（Root Mean Square Error）［20］作为光伏电站功率预测误差的评价指标。

在测试集中根据NWP 广义天气类型和公共气象服务预报的广义天气类型对总辐照度进行修正，共分为附录D 表D2 所示的7 种情况。表中：“一步修正”表示修正系统误差，“两步修正”表示修正系统误差后进一步按照转移概率进行修正；仅情况5—7需要计算广义天气类型的转移概率和总辐照度等级，进行两步修正；情况1—4中NWP 广义天气类型与公共气象服务预报的广义天气类型相同，只需根据对应的广义天气类型修正总辐照度系统误差；每种情况分别选取1 d 作为典型日。图6 为广义天气类型1 典型日总辐照度修正及功率预测结果，其他广义天气类型典型日总辐照度修正及功率预测结果见附录D 图D4—D6。表5 为不同广义天气类型下的功率预测误差。

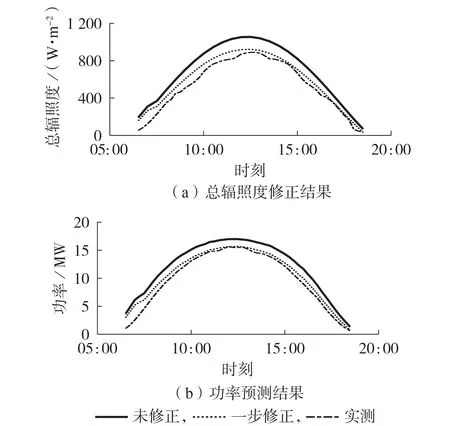
图6 广义天气类型1总辐照度修正及功率预测结果Fig.6 Total irradiance correction and power forecasting results for Generalized Weather Type 1

由表5 可以看出，所有广义天气类型下以NWP修正系统误差后的总辐照度作为功率预测的数据源，预测准确度大幅提升，验证了本文所提的NWP总辐照度系统误差计算方法的有效性。

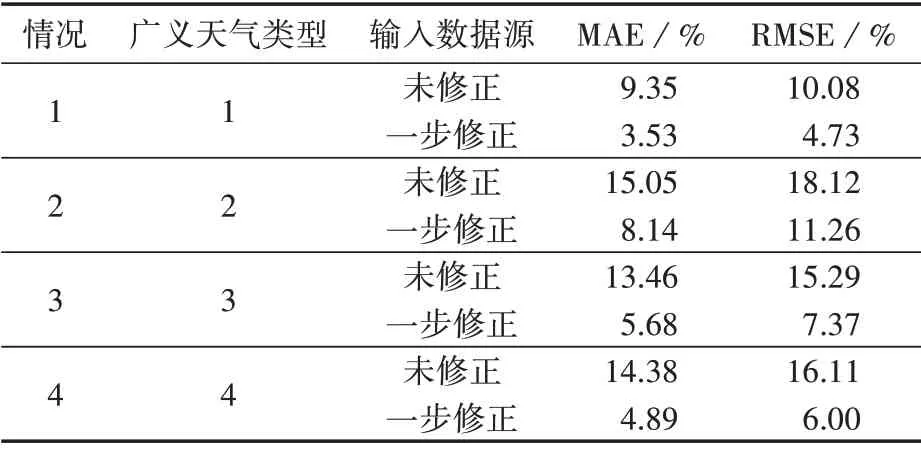
表5 不同广义天气类型下的功率预测误差Table 5 Power forecasting errors under different generalized weather types

情况5—7 中NWP 划分的广义天气类型与公共气象服务预报的广义天气类型不同，需要在修正系统误差的基础上进一步依据预测日不同广义天气类型的转移概率修正NWP 总辐照度值。图7 为情况5对应的总辐照度修正及功率预测结果。情况6 和情况7 对应的总辐照度修正及功率预测结果分别见附录D图D7和图D8。

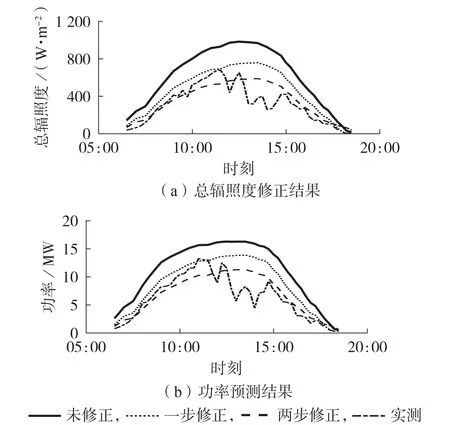
图7 2019年5月5日总辐照度修正及功率预测结果Fig.7 Total irradiance correction and power forecasting results on May 5，2019

针对情况7 对应的2019 年5 月4 日进行分析说明。该日NWP 广义天气类型为广义天气类型4，公共气象服务预报的广义天气类型为广义天气类型2。按照广义天气类型4 修正总辐照度系统误差后得到的功率预测结果与实测功率相差较大，这是由NWP 广义天气类型预报错误，对总辐照度修正过度导致的。通过广义天气类型2与4之间的折算系数和2 种广义天气类型转移概率计算融合2 种气象预报进行修正后的总辐照度序列，拉升了按广义天气类型4 进行系统误差修正后的总辐照度曲线，按该总辐照度曲线得到的功率预测结果与实测功率的误差相比仅进行系统误差修正大幅减小。附录D 表D3为情况5—7典型日预测误差。由表可知，当预测日NWP划分的广义天气类型与公共气象服务预报的广义天气类型不一致时，按照本文提出的两步修正方法修正NWP 总辐照度，并将其作为预测模型的输入源，得到的预测结果误差更小，验证了本文所提出的依据转移概率对总辐照度进行进一步修正的有效性。

在测试集31 d 中：NWP 广义天气类型与公共气象服务预报的广义天气类型一致的共有17 d，对于该类预测日的NWP 总辐照度，只需修正系统误差；NWP 广义天气类型与公共气象服务预报的广义天气类型不一致的共有14 d，对于该类预测日的NWP总辐照度，在修正系统误差之后，以各广义天气类型的转移概率为权重计算修正后的总辐照度。附录D表D4为测试集平均误差统计表。由表可知，从长时间范围看：NWP 总辐照度修正系统误差后比修正前预测结果的MAE 减小了6.48 %，RMSE 减小了6.19%；NWP 总辐照度两步修正后比修正前预测结果的MAE 减小了7.65%，RMSE 减小了7.66%；本文提出的NWP 总辐照度两步修正算法比仅修正NWP总辐照度系统误差预测结果的MAE 减小了1.17%，RMSE 减小了1.47%。测试集31 d 预测结果的月RMSE 为9.91%，完全满足我国现行标准NB／T 32011—2013《光伏发电站功率预测系统技术要求》中规定的短期预测月RMSE小于15%的要求。

因此，本文提出的结合公共气象服务天气类型预报分步修正NWP 总辐照度可以显著提高功率预测的准确度，并有较高的工程应用价值。

6 结论

本文基于NWP和公共气象服务天气类型预报2种气象预报数据源，建立总辐照度修正的光伏功率短期预测模型，该模型由光伏电站历史数据分类模型、NWP 广义天气类型分类模型、广义天气类型转移概率计算模型、NWP 总辐照度修正模型和GA-BP神经网络预测模型组成。从测试集31 d 的预测结果来看，相较于传统以未处理的NWP 数据和仅修正NWP 系统误差后的数据进行功率预测的方法，本文所建立的预测模型MAE 分别减小了7.65% 和1.17%，RMSE分别减小了7.66%和1.47%，且月RMSE为9.91%，满足我国现行标准的要求，验证了所建立的光伏功率短期预测模型的有效性，为使用NWP 进行功率预测提供了一种新思路。

本文建立的总辐照度修正模型以d 为单位，以修正后的总辐照度预测光伏功率，在一定程度上提高了功率预测的精度。但在长时间尺度上总辐照度修正标准单一，未来可将研究重点转向将预测日全天划分为不同时段分别进行修正，以进一步提升预测精度。

附录见本刊网络版（http：//www.epae.cn）。