几乎弱θ加细空间
代晓琴,叶 斌,高绍娟,康素玲
(1.成都理工大学信息管理学院,四川成都 610059;2.合肥学院数学与物理系,安徽合肥 230601)
0 引 言
如果 X的每个离散闭集族{Fα:α∈n}存在 X的稠密子集D和X的开集族V=n∪∈ωVn,使得 ∀n∈ω,∀α∈∧有 Fα⊂Vnα,并且对 ∀x∈D,存在n∈ω,且有1≤ord(x,Vn)<ω.
引理1[3]设λ是一个基数,空间X是λ—仿紧的,∧是一个定向集,|∧|=λ,如果{Hα:α∈∧}是 X的一个定向上升覆盖,则存在 X的定向上升开覆盖{Kα:α=∧},使得对α∈∧有⊂ Hα.
引理2 几乎弱θ加细空间的闭子空间是几乎弱θ加细的.
文中所讨论的拓扑空间均为 Hausdorff空间(简称空间),并且用(U)A和N(A)表示集族{U∈U;U∩A≠φ}和集合A的开领域系.特别地,(U)x和N(x)分别表示(U){x}和N({x});st{A,U}=∪{U∈U: U∩A≠φ},特别地,st(x,U)表示st({x},U);A—表示集合A的闭包,|∧|表示集合 ∧的基数;ω表示非负整数集或最小无限基数;[A]<ω={F⊂A:F是非空有限集},对于 n∈ω,s=(n0…,nk)∈[ω]<ω,记 s⊕ n=(n0…,nk,n).本文涉及的其他有关概念、记号和表示方法参照文献[1]和[2]中的相关规定.
定义1 集族T称为是定向的,如果 ∀S,S′∈T,存在T∈T,使得,S∪S′⊂T.设(∧,≤)是一个定向集,集族U={Uα:α∈∧}是定向上升的,如果对 ∀α,β∈∧,当α≤β时,有 Uα⊂Uβ.
定义2[1]设λ是一个基数,并且λ≥2,空间X称为λ—仿紧的,如果X的每个势 ≤λ的开覆盖有一个局部有限的开加细.
定义3 空间X称为是几乎弱θ加细空间,当且仅当X的每个开覆盖U都存在X的一个稠密子集D和U的开加细V=n∪∈ωVn对于 ∀x∈D,存在 n∈ω且有1≤ord(x,Vn)<ω.
定义4 空间X称为是几乎离散弱θ可膨胀的,
1 主要结果
定理1 空间X几乎弱θ加细的,当且仅当X是几乎离散弱θ可膨胀的,并且X的每个开覆盖,U= {Uα:α∈∧},都存在X的稠密子集D和U的开加细V=n∪∈ωVn,使得x∈D,存在n∈ω和α∈∧,有 ∀x∈Vα,并且,st(x,Vn)⊆β∪≤αUβ.
证明 (⇒)是显然的,下面证明(⇐).
设U是X的任一开覆盖,∀U∈U,令M(U,U) =X-∪(U′∈U:U′≠U),则有:
(1){M(U,U):U∈U}是 X中的闭集族,并且对U∈U,当M(U,U)≠φ时,有∪{U′∈U:M(U, U)∩U′≠φ}=U.


(2)n∪∈ω(Ut⊕n∪Wt⊕n)是 X的开覆盖,并且n∪∈ω(Ut⊕n∪Wt⊕n)是U的开加细,故构造出U的开加细,n∪∈ω{Us∪Ws:s∈[ω]<ω}.于是,归纳定义完成.
(3)∀x∈D*,存在 s∈[ω]<ω,使得1≤ord(x,Us∪WS)<ω.
事实上,对 ∀k∈ω用归纳法定义sk∈[ω]<ω, αk<λ,s0=φ,如果,sk已经有定义,则由 *—加细的定义,存在n∈ω和0≤αk<λ,使得,x∈Uαk,Sk, st(x,VSk⊕n) ⊂β∪≤αUβ,Sk,并且集族{U ∈USk:x∈st(M(U,USkUWSk),VSk⊕n)}是有限的.设,sk+1=sk⊕n,则对 ∀k∈ω,有1≤ord(x,WSk)<ω.

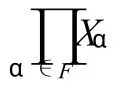
(1)UFζ开于YF并且UFζ×ZF⊂ Uζ,令,OF= (α∈∪∧UFζ×ZF).

(3)因X是|∧|—仿紧的,根据引理1,存在X的开覆盖{GF:F∈[∧]<ω},使得,∀F∈[∧]<ω, G—F⊂ GE,且 ∀E,F∈[∧]<ω,若 F⊂ E,则GF⊂GE,∀F∈[∧]<ω.

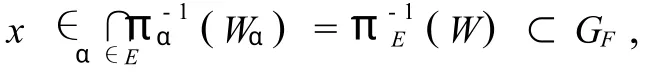
(6)对 ∀n∈ω,令Hn={π-F1(VFnζ)∩KF:F∈[∧]<ω,ζ∈ ∑VFnζ∈VFn}〈,Hn〉n∈ω是U={Uζ: ζ∈∑}的开加细序列.首先,∀x∈X,因{KF:F∈[∧]<ω}是 X的开覆盖,故,∃F∈[∧]<ω,得 x∈KF,并且对于 ∀n∈ω,VFn={VFnζ:ζ∈∑}是TF的开覆盖,则对 ∀n∈ω,使πF(x)=xF∈FFnζ,即 x∈π-F1(UFα)∩KF.其次,∀n∈ω,因 VFnζ⊂UFζ,π-F1(VFnζ)∩KF⊂π-F1(UFζ)⊂ UFζ×ZF⊂ Uζ.故,〈Hn〉n∈ω是U={Uζ:ζ∈∑}的开加细.
(7)对于 ∀F∈[∧]<ω,∃n∈ω,使得1≤ord(x,Hn)<ω.事实上,∀x∈π-1F(DF),则,x∈KF⊂CF=(IntTF)×ZF.故对 ∀n∈ω,∀Fn,存在n∈ω,使得1≤ord(xF,VFn)<ω,并且(Hn)x= {π-1F(VFζ)∩KF:VFnζ∈(VFn)xF}.即,∃n∈ω,有1≤ord(x,Hn)<ω,从而 X是几乎弱θ加细的.
[1]蒋继光.一般拓扑学选讲[M].成都:四川教育出版社, 1991.
[2]Engeking R.General Topology[M].Marszawa:Polish Scientific Pulisher,1977.
[3]Chiba K.Normality of Inverse Limits[J].Math Japonica,1990, 35(5):959-970.
[4]Grabner E,Grabner G.Nearly Metacompact Spaces[J].T opology Appl,1999,98(1):191-201.
[5]高国士.拓扑空间论[M].北京:科学出版社,2001.
[6]Kemoto N,Yajina Y.Orthocompactness in Products[J].Tsukuba J Math,1992,16(2):407-422.
[7]曹金文.几乎仿紧空间[J].纯粹数学与应用数学,2003,19 (1)57-60.

