The Sufficient and Necessary Condition of Lagrange Stability of Quasi-periodic Pendulum Type Equations∗

CONG FU-ZHONG,LIANG XINAND HAN YUE-CAI

(1.Fundamental Department,Aviation University of Air Force,Changchun,130022)

(2.Institute of Mathematics,Jilin University,Changchun,130012)

The Sufficient and Necessary Condition of Lagrange Stability of Quasi-periodic Pendulum Type Equations∗

CONG FU-ZHONG1,2,LIANG XIN1AND HAN YUE-CAI1

(1.Fundamental Department,Aviation University of Air Force,Changchun,130022)

(2.Institute of Mathematics,Jilin University,Changchun,130012)

The quasi-periodic pendulum type equations are considered.A sufficient and necessary condition of Lagrange stability for this kind of equations is obtained. The result obtained answers a problem proposed by Moser under the quasi-periodic case.

Lagrange stability,pendulum type equation,KAM theorem

1 Introduction

The Lagrange stability of pendulum type equations is an important topic,which is proposed by Moser[1].Moser[2],Levi[3]and You[4]investigated such topic for the periodic situation, respectively.In particular,You obtained a sufficient and necessary condition for Lagrange stability of the equation(1.1)in[4].

Recently,Bibikov[5]developed a KAM theorem for nearly integrable Hamiltonian systems with one degree of freedom under the quasi-periodic perturbation.In fact,his KAM theorem is of parameter type.Using this theorem he discussed the stability of equilibrium of a class of the second order nonlinear differential equations.

In this note we study quasi-periodic pendulum type equations.Under the standard Diophantine condition of frequency ω,a sufficient and necessary condition of Lagrange stability for quasi-periodic pendulum type equations is obtained.This answers Moser’s problem under the quasi-periodic case.

We consider a nonlinear pendulum type equation

and p(t,x)is a quasi-periodic function in t with basic frequencies ω=(ω1,···,ωn),that is,

for some function f(θ,x)de fi ned on Tn×T1.Here Tn=Rn/Znis an n-dimensional torus.

Assume that f(θ,x)is a real analytic function on Tn×T and the frequency ω satis fies Diophantine condition as follows:

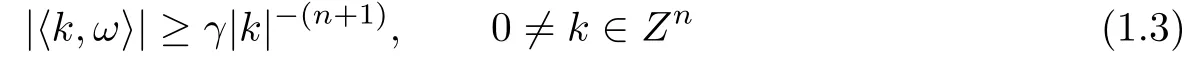
for a given γ＞0,where h·,·i denotes the usual inner product.

We are in a position to state the main result of this paper.

Theorem 1.1 Assume that(1.3)holds.Then system(1.1)is Lagrange stable if and only if Z

Moreover,if(1.3)and(1.4)hold,equation(1.1)possesses in finitely many quasi-periodic solutions with n+1 basic frequencies(including ω1,···,ωn).

•Diophantine condition(1.3)can be replaced by a general form

with some constant τ∗＞n.Here we assume(1.3)for the convenience of the proof of Theorem 1.1.

•Huang[6]considered a class of almost periodic pendulum-type equations.He proved the existence of unbounded solutions of the equations.Summing up the works developed by Mose[2],Levi[3],You[4]and Huang[6],respectively,and Theorem 1.1,we can obtain a satisfactory answer to Moser’s problem.

•Recently,Lin and Wang[7]have concerned with a dual quasi-periodic system as follows:

where g(t,x)is quasi-periodic in t and x with frequencies Ω1=(ω1,···,ωn)andΩ2=(ωn+1,···,ωn+m),respectively.Under the assumptions

they proved that all the solutions of(1.6)are bounded(see[7]).It is easy to find that as m=1,their modi fi ed Diophantine condition is stronger than(1.5);in addition, the result of[7]is a sufficient condition to ensure Lagrange stability.This di ff ers from Theorem 1.1.

•In[8]and[9],the authors developed a quasi-periodic monotonic twist theorem.For the sake of simplicity,we should apply Bibikov’s lemma to prove our theorem,but apply the monotonic twist theorem.

2 A KAM Theorem under Quasi-periodic Perturbations

In this section we give a KAM theorem with a quasi-periodic perturbation by using Bibikov’s lemma(see[5]).

Let us consider a Hamiltonian system with Hamiltonian

where P(x,y,θ)is a function de fi ned on T1×R1×Tn,and ω satis fies(1.3).Assume that P is real analytic,that is,there is δ＞0 such that P is analytic on(T1×R1×Tn)+δ.Here D+δ is a complex neighborhood of D in Crfor any given subset D in Rrand fixed δ＞0. Let

Theorem 2.1There exists ε0＞0 depending only on γ,δ and n such that,for any interval(a,b),if|P|≤ε0on(T1×(a,b)×Tn)+δ,the following conclusions hold:

In order to prove Theorem 2.1 we need the following Bibikov’s lemma.

Bibikov’s Lemma[5]1)There exits ǫ0＞0 depending only on δ0,ι0and n such that if |P|＜ǫ0on D0,then there exist a function τ0:Aγ→R and a nearly identical transformation of coordinates

3Some Lemmas

This section is devoted to established some lemmas which will be used in the proof of Theorem 1.1.

4 Proof of Theorem 1.1

[1]Moser,J.,Stable and Random Motions in Dynamical Systems,Ann.Math.Stud.,Princeton Tokyo,1973.

[2]Moser,J.,A stability theorem for minimal foliations on a torus,Ergodic Theory Dynam.Systems, 8(1988),251–281.

[3]Levi,M.,KAM theory for particles in periodic potentials,Ergodic Theory Dynam.Systems, 10(1990),777–785.

[4]You,J.G.,Invariant tori and Lagrange stability of pendulum-type equations,J.differential Equations,85(1990),54–65.

[5]Bibikov,Yu.N.,On stability of zero solution of essential nonlinear Hamiltonian and reversible systems with one degree of freedom,differentsial’nye Uravneniya,38(2002),579–584.

[6]Huang,H.,Unbounded solutions of almost periodically forced pendulum-type equations,Acta Math.Sinica,17(2001),391–396.

[7]Lin,S.S.and Wang,Y.Q.,Lagrangian stability of a nonlinear quasi-periodic system,J.Math. Anal.Appl.,293(2004),258–268.

[8]Levi,M.and Zehnder,E.,Boundedness of solutions for quasiperiodic potentials,SIAM J.Math. Anal.,26(1995),1233–1256.

[9]Zharnitsky,V.,Invariant curve theorem for quasiperiodic twist mappings and stability of motion in the Fermi-Ulam problem,Nonlinearity,13(2000),1123–1136.

Communicated by Li Yong

37J40

A

1674-5647(2010)01-0076-09

date:April 21,2009.

Partially supported by the NSF(10871203,10601019)of China and the NCET(07-0386) of China.