Contact Finite Determinacy of Relative Map Germs∗

CHEN LIANG,SUN WEI-ZHIAND PEI DONG-HE

(1.School of Mathematics and Statistics,Northeast Normal University,Changchun,130024)

(2.School of Science,Changchun University of Science and Technology,Changchun,130022)

Contact Finite Determinacy of Relative Map Germs∗

CHEN LIANG1,SUN WEI-ZHI2AND PEI DONG-HE1

(1.School of Mathematics and Statistics,Northeast Normal University,Changchun,130024)

(2.School of Science,Changchun University of Science and Technology,Changchun,130022)

The strong contact finite determinacy of relative map germs is studied by means of classical singularity theory.We first give the de fi nition of a strong relative contact equivalence(orKS,Tequivalence)and then prove two theorems which can be used to distinguish the contact finite determinacy of relative map germs,that is, fis finite determined relative toKS,Tif and only if there exists a positive integerk, such thatMk(n)E(S;n)p⊂TKS,T(f).

KS,Tequivalent,the tangent space of an orbit,relative deformation, finite determined relative toKS,T

1 Introduction

A basic idea in the classical singularity theory is that local topological properties of a generic differentiable mapping are determined by finite terms of its Taylor series,i.e., finite determinacy of map germs.It relates to the most important local characteristics of the singularity theory.Therefore, finite determinacy is always an active research subject in the singularity theory.When we treat various spaces of differentiable mappings with several constraints,depending on situations,we need to study the corresponding finite determinacy,whose validity depends on given mapping spaces.

In the present paper we treat the space of differentiable mappings between manifolds with the constraint that a fixed submanifold is mapped into another fixed submanifold. Then naturally we need to study the“relative finite determinacy”.

There are several works studying relative finite determinacy of function germs,for instance[1]–[7].However,the study of relative finite determinacy of map germs such as[8]is very few.This paper is a sequel to[8].The purpose of the present paper is to give an algebraic criterion for relative contact finite determinacy of relative smooth map germs.It is a generalization of the algebraic criteria for K finite determinacy of smooth map germs originated in[9].

This paper is organized as follows:In Section 2 we give some notations,de fi nitions and other related knowledge.Section 3 is the main part of this paper.We prove the main results in a similar way to[9].

2 Preliminaries

Let S,T be submanifolds without boundary ofRnandRprespectively,both contaning the origin.Denote by M(Rn,S;Rp,T)the set of relative smooth mappings f:(Rn,S)→(Rp,T)with f(S)⊂T and f(0)=0.For f,g∈M(Rn,S;Rp,T),we call f,g equivalent near the origin if f=g on some neighborhood of the origin in Rn.This equivalence class of f is called a relative map germ and denoted by[f].In this paper we also denote it by f for convenience.We only consider the local case,so we may assume that

Denote by M∗=M(n,s;p,t)the set of relative map germs and Ef∗=E(f,n,s;p,t)the set of relative map germs g which satis fies g(S)=f(S)for a given f∈M∗.Let

be a local ring and

be the maximal ideal of CS(Rn).Similarly,we can de fi ne the set CT(Rp)and E(T;p).For f∈M∗,it induces a homomorphism f∗:CT(Rp)→CS(Rn)de fi ned by f∗(h)=h◦f with f∗E(T;p)⊆E(S;n).Every CS(Rn)-module can be viewed as a CT(Rp)-module through f∗.We denote

We can also denote by

the strong relative contact equivalent group,where KS,Tacts on M∗in a natural way:If f∈M∗,H∈KS,T,then H·f is de fi ned by

where h:(Rn,0)→(Rn,0),h(x)=x,for any x∈S is a di ff eomorphism ofRndecided only by H and1:(Rn,0)→(Rn,0)is the identity map germ.We also observe that KS,Tis a subgroup of the general contact equivalent group K in[9].More details can be found in [8]and[9].

De fi nition 2.1We say that two relative map germsf,g∈M∗are strong relative contact equivalent if there existsH∈KS,Tsuch thatg=H·f.We also call thatfandgareKS,Tequivalent.

De fi nition 2.2Letf∈M∗.The tangent space ofKS,Torbit of f is the vector space

De fi nition 2.3Letf∈M∗.We call the map germF:(R×Rn,R×S)→(Rp,T),(t,x)7→F(t,x)a1-parameter relative deformation offifFsatis fies

De fi nition 2.4We callF:(Rn×R,S×R)→(Rp×R,T×R)a level preserving map germ ifF(x,t)=(Fa(x,t),t),whereFa:(Rn×R,S×R)→(Rp,T)satis fies

De fi nition 2.5Supposekis a nonnegative integer.Thenf∈M∗iskdetermined relative toKS,T(abbreviated ask.det.rel.KS,T)if for anyg∈Ef∗withjkg(0)=jkf(0),theKS,Torbit offcontainsg,i.e.,fandgareKS,Tequivalent.

3 Finite Determinacy Relative to KS,T

In this section,we give two algebraic criterions for judging whether or not a relative map germ is finite determined relative to KS,T.

Lemma 3.1[8]Letf,g∈M∗withjkf(0)=jkg(0).Then

Theorem 3.1Letf∈M∗,S={0}×Rn−s,andT={0}×Rp−t.Iffiskdetermined relative toKS,T,then there exists a positive integerksuch that

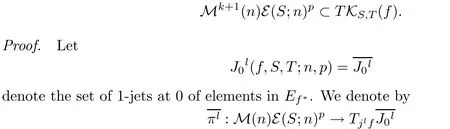
the canonical projection.

Since f is k determined relative to KS,T,for all g∈Ef∗,with jkg(0)=jkf(0),the KS,Torbit of f contains g.We have

and then taking tangent spaces at jlf on both sides,we have

Obviously,the right hand side of the last formula is a CS(Rn)-module.Let l=k+1.By the Nakayama Lemma,we have

Theorem 3.2If there exists a positive integerksuch thatMk(n)E(S;n)p⊂TKS,T(f),thenfis(k+1)determined relative toKS,T.

Proof.Let g∈M∗satisfy jlg(0)=jlf(0).For any t0∈R,let

In the following,we prove that Ftand Ft0are KS,Tequivalent for any t in a neighborhood J of t0.To see this,we only need to prove that there exists two level preserving map germs H and H′which satisfy the following conditions:

We observe that Htis determined only by,so our problem turns to construct a smooth map germ H′twhich satis fies conditions(1)–(3).We claim that it suffice to construct a smooth vector field germΘat the origin ofRn×Rpfor which

(A)ξi(x)=0,for any x∈S,ηj(x,y)=0,for any x∈Rn,y∈T;

Since if such a vector field germΘexists,by integrating this vector field,it has a flow, i.e.,a map germ H′tof the required type,which can be supposed to satisfy the“initial condition”(1).A minor computation shows that the conditions(2),(3)are also satis fi ed.

It remains to prove the existence of a vector field germΘwhich having the properties (A),(B).Since Mk(n)E(S;n)p⊂TKS,T(f),g∈Ef∗and jlg(0)=jlf(0),by Lemma 1.1 we have

[1]Porto,P.F.S.and Loibel,G.F.,Relative finite determinacy and relative stability of functiongerms,Bol.Soc.Brasil Mat.,9(1978),1–18.

[2]Porto,P.F.S.,On relative stability of function-germs,Bol.Soc.Brasil Mat.,14(1983),99–108.

[3]Izumiya,S.and Matsuoka,S.,Note on smooth function germs on varieties,Proc.Amer.Math. Soc.,97(1986),146–150.

[4]Kushner,L.,Finite determination on algebraic sets,Trans.Amer.Math.Soc.,331(1992),553–561.

[5]Kushner,L.and Leme,B.T.,Finite relative determination and relative stability,Paci fi c.J. Math.,192(2000),315–328.

[6]Sun,B.and Wilson,L.C.,Determinacy of smooth germs with real isolated line singularities,Proc.Amer.Math.Soc.,129(2001),2789–2797.

[7]Grandjean,V.,Finite determinacy relative to closed and finitely generated ideals,Manuscripta Math.,103(2000),313–328.

[8]Chen,L.,Sun,W.Z.and Pei,D.H.,Strong relative finite determinacy of map germs(in Chinese),Dongbei Shida Xuebao,36(2004),16-20.

[9]Mather,J.N.,Stability of C∞mappings,III:Finitely determined map germs,Inst.Hautes Etudes Sci.Publ.Math.,35(1969),279–308.

Communicated by Lei Feng-chun

58C27

A

1674-5647(2010)01-0001-06

date:Sept.17,2007.

Science Foundation(20070105)for Young Teachers of Northeast Normal University.