Convergence of Online Gradient Method with Penalty for BP Neural Networks∗

SHAO HONG-MEI,WU WEIAND LIU LI-JUN

(1.College of Mathematics and Computational Science,China University of Petroleum,

Dongying,Shandong,257061)

(2.Department of Applied Mathematics,Dalian University of Technology,

Dalian,Liaoning,116024)

(3.Department of Mathematics,Dalian Nationalities University,Dalian,Liaoning,116605)

Convergence of Online Gradient Method with Penalty for BP Neural Networks∗

SHAO HONG-MEI1,WU WEI2AND LIU LI-JUN3

(1.College of Mathematics and Computational Science,China University of Petroleum,

(2.Department of Applied Mathematics,Dalian University of Technology,

(3.Department of Mathematics,Dalian Nationalities University,Dalian,Liaoning,116605)

Online gradient method has been widely used as a learning algorithm for training feedforward neural networks.Penalty is often introduced into the training procedure to improve the generalization performance and to decrease the magnitude of network weights.In this paper,some weight boundedness and deterministic convergence theorems are proved for the online gradient method with penalty for BP neural network with a hidden layer,assuming that the training samples are supplied with the network in a fixed order within each epoch.The monotonicity of the error function with penalty is also guaranteed in the training iteration.Simulation results for a3-bits parity problem are presented to support our theoretical results.

convergence,online gradient method,penalty,monotonicity

1 Introduction

Online gradient method(OGM for short)is a popular and commonly used learning algorithm for training the weights of BP networks(see[1]–[5]).Penalty methods are often introduced into the training procedure and have proved efficient to improve the generalization performance and to decrease the complexity of neural networks(see[6]–[12]).Here the generalization performance refers to the capacity of a neural network to give correct outputs for untrained data.A simple and commonly used penalty added to the conventional error function is the squared penalty,a term proportional to the magnitude of the network weights(see[2]and[3]).Applied to the weight updating rule of batch gradient descent algorithm, the in fl uence of penalty on the training can be seen clearly:

where w,∆w(n),E(w),η and λ represent the vector of all weights,the modi fi cation of w at the n-th iteration,the conventional error function,the learning rate and the penalty parameter,respectively.As shown in(1.1),in addition to the update by the gradient algorithm,the weight is decreased by λ times of its old value.Consequently,the weights with small magnitudes are encouraged to decrease to zero and those with large magnitudes are constrained from growing too large during the training process.This will force the network response to be smoother and less likely to over fi t,leading to good generalization (see[6],[7]and[11]).Many experiments have shown that as well as being bene fi cial from a generalization capacity prospective,such a term provides a way to control the magnitude of the weights during the training procedure in literature(see[6]and[10]–[12]).But there remains a lack of theoretical assurance on this experimental observation,especially for online cases.

For simplicity of analysis,the input sample ξjis provided to the network in a fixed order in each training epoch.We shall show that the online gradient method with penalty and fixed inputs(OGM-PF)is deterministically convergent.A boundedness theorem is established for the network weights connecting the input and hidden layers,which is also a desired outcome of adding penalty.Another key point of our proofs lies in the monotonicity of the error function with such a penalty term during the training iteration.

The rest of this paper is organized as follows.OGM-PF is described in detail in Section 2.The main theorems are presented in Section 3.In Section 4,the algorithm OGM-PF is applied to a 3-bits parity problem to illustrate our theoretical findings.Some lemmas and detailed proofs of the theorems are gathered as an Appendix.

2 Online Gradient Method with Penalty

Consider a three-layer BP network consisting of p input units,q hidden units and one output unit.Let w0=(w01,···,w0q)be the weights between the hidden units and the output unit, and wi=(wi1,···,wip)be the weights between the input units and the hidden unit i(i= 1,2,···,q).To simplify the presentation,we write all the weight parameters in a compact form,i.e.,W=(w0,w1,···,wq)∈Rq+pq.And we de fi ne a matrix V=(,···,)T∈Rq×pand a vector function G(x)=(g(x1),···,g(xq))for x=(x1,···,xq)∈Rq.Assume that{ξj,Oj}Jj=1is the given set of training samples and g:R→Ris a transfer function for both hidden and output layers.Then for each input ξ∈Rp,the actual output vector of the hidden layer is G(V ξ)and the fi nal output of the network is ζ=g(w0·G(V ξ)).A

conventional square error function is given by

By adding a penalty term,the total error function takes the form(see[3])

differentiating E(W)with respect to W gives

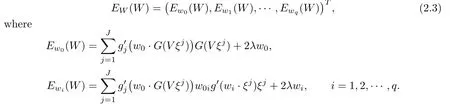
The online gradient algorithm updates the weights after the presentation of each training sample ξj.As done in[13],we can choose the training samples in a fixed order and the online gradient method with penalty(OGM-PF)can be described as follows:

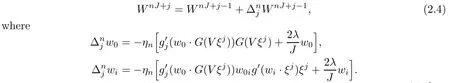
Here ηnis the learning rate in the n-th training epoch.From an initial value η0∈(0,1],it changes its value after each epoch of training according to(see[13]and[14])

where β＞0 is a constant to be speci fi ed in assumption(A3)below.

3 Main Theorems

The following assumptions are needed.

(A1) |g(t)|,|g′(t)|and|g′′(t)|are uniformly bounded for t∈R.

contains only finite points.

Remark 3.1We note that from(2.2)and(A1),the functions|gj(t)|,(t)|and(t)| are also uniformly bounded for all t and j.

Theorem 3.1(Monotonicity)Let the error functionE(W)be given in(2.2),the learning rates{ηn}be determined by(2.5),W0be an arbitrary initial value,and the weights{Wk}be generated by the algorithm OGM-PF(2.4).If assumptions(A1)–(A3)are valid,then

Theorem 3.2(Boundedness)Under the same assumptions of Theorem3.1,the weight sequencesconnecting the input and hidden layers is uniformlybounded.

Theorem 3.3(Convergence)Let the error functionE(W)be de fi ned in(2.2)and the weights{Wk}be updated by the algorithm OGM-F(2.4).If assumptions(A1)–(A3)are satis fi ed,then there holds the following weak convergence result:

Furthermore,if assumption(A4)is also valid,we have the strong convergence:There existsW∗∈Φ0such that

4 Numerical Experiment

To demonstrate the convergence behavior of the online gradient method with penalty used in this paper,a benchmark problem−parity problem is simulated.The parity problem is a well-known difficult problem that has often been used for testing the performance of network training algorithm.

The input set consists of 2npatterns in n-dimensional space and each pattern is an n-bit binary vector.The target value Ojis equal to 1 if the number of 1 in the pattern is odd, otherwise it is equal to 0.For simplicity,in this experiment we use the 3-bit parity problem which can be solved by a three-layer network with the structure 3-3-1.The transfer function for both the hidden layer and output layer is chosen to be logsig(·).This test is carried out by setting the initial learning rate η0and the penalty parameter λ with different values, varying from 0.9 to 0.5,and 0.01 to 0.001,respectively.For every combination of different η0and λ,the training starts with the same initial weights.

Since the changes of total error(see(2.2))and network weights become quite tiny when the number of iteration exceeds 200,and their convergence performances are similar,we just lay out the observation with η0=0.8 in the first 200 epoches.

As shown in Fig.4.1,the total error with penalty decreases monotonically and the corresponding gradient tends to zero as the number of iteration increases.The restraint of the penalty term on the magnitude of the weights is shown in Fig.4.2.Without penalty, the weight becomes larger and larger during the training iteration,while the magnitude of the weights is e ff ectively reduced and fi nally tends to keep steady after adding the penalty. Table 4.1 summarizes the results obtained at the 200-th iteration by taking different penalty parameters,from which we see that the larger λ is,the smaller the weight becomes.Hence, the penalty approach provides a mechanism to e ff ectively control the magnitude of the weights.

Fig.4.1 Total error and norm of gradient with penalty

Fig.4.2 E ff ect of λ on error and weight

Table 4.1 E ff ect of λ on error and weight

5 Appendix

We introduce the following notations to simplify arguments:

Lemma 5.1Let{ηn}be given by(2.5).Then the following estimates hold:

Proof.This lemma can be proved by using(2.5)and η0∈(0,1].

Next,we present a few more lemmas.Their proofs are omitted to save the space.Proofs for similar results can be found in[13]and[14].

Lemma 5.2Let assumptions(A1)and(A2)be valid.There areCi＞0such that

Lemma 5.3There exists a positive constantγindependent ofnsuch that

In virtue of(5.10),Theorem 3.1 can be proved if for any nonnegative integer n there holds

For n=0,if the left side of(5.11)is zero,then

Hence,we have already reached a local minimum of the error function,and the iteration can be terminated.Otherwise,

will be satis fi ed for all small enough η0.In this case,we can prove(5.11)by applying an induction on n,resulting in the next lemma.

Lemma 5.4Let assumptions(A1)and(A2)be satis fi ed and{ηn}be updated by(2.5). Then there exists a constantβ0such that if the initial learning rateη0and the constantβin(2.5)satisfy Assumption(A3),then(5.11)holds for alln.

The next two lemmas are necessary to our convergence result.Their proofs are omitted since they are quite similar to those of Lemma 3.5 in[14]and Theorem 14.1.5 in[15](also in[16]),respectively.

Lemma 5.6LetF:Ω⊂Rn→Rm(n,m≥1)be continuous(Ω⊂Rnis a closed bounded region)and Ω0={x∈Ω:F(x)=0}be finite.Suppose that the sequence{xk}⊂Ωis such that

Now we are ready to prove Theorems 3.1–3.3.

Proof of Theorem 3.1The monotonicity theorem can be drawn directly from(5.12), Lemma 5.3 and Lemma 5.4.

Proof of Theorem 3.2In light of(2.2)and(3.1),there holds for all n=0,1,···and i=1,2,···,q that

It follows from(5.12)and Lemma 5.4 that σn≥0 for all n=0,1,···.By virtue of(5.10) we can write

The proof of the strong convergence can be done as that of Theorem 3 in[17],and the detail is omitted.

[1]Rumelhart,D.E.,McClelland,J.L.and the PDP Research Group,Parall Distributed Processing-Explorations in the Microstructure of Cognition,Mass.,MIT Press,Cambridge, 1986.

[2]Haykin,S.,Neural Networks:A Comprehensive Foundation,Macmillan,New York,1994.

[3]Hinton,G.E.,Connectionist learning procedures,Artif.Intell.,40(1989),185–234.

[4]Sollich,P.and Barber,D.,Online learning from finite training sets and robustness to input bias,Neural Comput.,10(1998),2201–2217.

[5]Luo,Z.,On the convergence of the LMS algorithm with adaptive learning rate for linear feedforward networks,Oper.Res.,3(1991),226–295.

[6]Setiono,R.,A penalty-function approach for pruning feedforward neural networks,Neural Comput.,9(1997),185–204.

[7]Reed,R.,Pruning algorithms–a survey,IEEE Trans.Neural Networks,4(1993),740–747.

[8]Chen,Z.and Haykin,S.,On different facets of regularization theory,Neural Comput., 14(2002),2791–2846.

[9]Ishikawa,M.,Structural learning with forgetting,Neural Networks,9(1996),509–521.

[10]Cho,S.and Chow,T.W.,Training multilayer neural networks using fast global learning algorithm–least squares and penalized optimization methods,Neurocomputing,25(1999),115–131.

[11]Takase,H.,Kita,H.and Hayashi,T.,E ff ect of regularization term upon fault tolerant training,Proc.Int.Joint Conf.Neural Networks,2(2003),1048–1053.

[12]Saito,K.and Nakano,R.,Second-order learning algorithm with squared penalty term,Neural comput.,12(2000),709–729.

[13]Wu,W.,Feng,G.,Li,Z.and Xu,Y.,Convergence of an online gradient method for BP neural networks,IEEE Trans.Neural Networks,16(2005),533–540.

[14]Wu,W.,Feng,G.and Li,X.,Training multilayer perceptrons via minimization of sum of ridge functions,Adv.Comput.Math.,17(2002),331–347.

[15]Ortega,J.M.and Rheinboldt,W.C.,Iterative Solution of Nonlinear Equations in Several Variables,Academic Press,New York,1970.

[16]Yuan,Y.and Sun,W.,Optimization Theory and Methods,Science Press,Beijing,2001.

[17]Wu,W.,Shao,H.and Qu,D.,Strong Convergence for Gradient Methods for BP Networks Training,Proc.Internat.Conf.Neural Network Brains(ICNNB’05),IEEE Press,2005,332–334.

Communicated by Ma Fu-ming

92B20,68T05

A

1674-5647(2010)01-0067-09

date:Dec.14,2007.

The NSF(10871220)of China and the Doctoral Foundation(Y080820)of China University of Petroleum.