Weighted Estimates for the Maximal Commutator of Singular Integral Operator on Spaces of Homogeneous Type∗

ZHANG HAO

(Department of Applied Mathematics,Information Engineering University,Zhengzhou,450002)

Weighted Estimates for the Maximal Commutator of Singular Integral Operator on Spaces of Homogeneous Type∗

ZHANG HAO

(Department of Applied Mathematics,Information Engineering University,Zhengzhou,450002)

Weighted estimates with general weights are established for the maximal operator associated with the commutator generated by singular integral operator and BMO function on spaces of homogeneous type,where the associated kernel satis fies the Hlder condition on the first variable and some condition which is fairly weaker than the Hlder condition on the second variable.

spaces of homogeneous type,weighted estimates,singular integral operator,commutator,maximal operator

1 Introduction

We work on a space of homogeneous type.Let X be a set endowed with a positive Borel regular measureµand a symmetric quasi-metric d satisfying that there exists a constant κ≥1 such that for all x,y,z∈X,

The triple(X,d,µ)is said to be a space of homogeneous type in the sense of Coifman and Weiss[1],ifµsatis fies the following doubling condition:there exists a constant C≥1 such that for all x∈X and r＞0,

Moreover,if C is the smallest constant for which the measureµveri fies the doubling condition,then D=log2C is called the doubling order ofµand we have

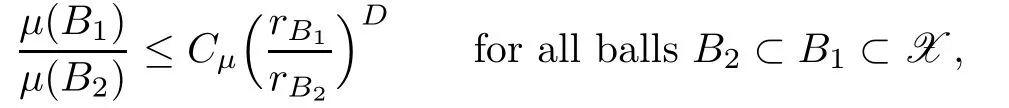
where rBidenotes the radius of Bi,i=1,2.

We remark that although all balls de fi ned by d satisfy the axioms of complete system of neighborhood in X,and therefore induce a topology in X,the balls B(x,r)for x∈X and r＞0 need not to be open with respect to this topology.However,by a remarkable result of Macas and Segovia in[2],we know that there exists another quasi-metric˜d which is equivalent to d such that the balls corresponding to˜d are open in the topology induced by˜d.Thus,throughout this paper,we assume that the balls B(x,r)for x∈X and r＞0 are open.

Let T be a linear L2(X)-bounded operator with kernel K in the sense that for all f∈L2(X)with bounded support and almost all x/∈suppf,

where K is a locally integrable function on X ×X{(x,y):x=y}.For b∈BMO(X), de fi ne the commutator generated by T and b by

where and in the following,L∞0(X)denotes the set of bounded functions with bounded support.The maximal operator associated with the commutator Tbis de fi ned by

with some η∈(0,1],for the operator T∗b,Hu and Wang[3]proved Lpweighted estimates with general weight,Huet al.[4]established weighted endpoint estimates with general weight. Whether one of the smoothness conditions can be replaced by the weaker one,it is of considerable interest.To state our result,we first give some notations.

Let E be a measurable set withµ(E)＜∞.For any fixed l＞0 and a suitable function f,set

The maximal operator ML(lgL)lis de fi ned by

where the supremum is taken over all balls containing x.Our main result can be stated as follows.

Theorem 1.1LetTbe a linearL2(X)-bounded operator with kernelKin the sense of(1.1)andb∈BMO(X).Suppose thatKsatis fies(1.4),(1.5)and the following condition

for anyR＞0andy,y′∈Xwithd(y,y′)＜R,whereCis independent ofx,y,y′andR. Then

Remark 1.1The iteration of the Hardy-Littlewood maximal operators on the right-hand sides of(1.8)and(1.9)are bigger than that of Theorem 1 in[3]and that of Theorem 1.3 in [4]respectively.We guess that this is due to the weaker smoothness condition on the second variable of the kernel K here.

Remark 1.2We do not know if there is a Cotlar inequality linking the operatorsand Tbwhen K satis fies(1.4),(1.5)and(1.7),so our argument in the proof of Theorem 1.1 is fairly different from which was used in[5].On the other hand,we do not have the sharp estimate as Lemma 3 in[3],so the theorem of Lerner in[6]cannot be applied directly.To overcome these difficulties,we use the sharp functionto estimatevia the Caldern-Zygmund decomposition.

We now make some conventions.Throughout this paper,we always denote by C a positive constant which is independent of the main parameters,but it may vary from line to line.Constant with subscript such as C2,does not change in different occurrences.For a measurable set E and a weight w,χEdenotes the characteristic function of E,and

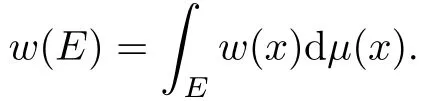
Given λ＞0 and a ball B,λB denotes the ball with the same center as B and whose radius is λ times that of B.For a fixed p with p∈(1,∞),p′denotes the dual exponent of p, namely,p′=p/(p−1).For a locally integrable function f on X and a bounded measurable set E,mE(f)denotes the mean value of f over E,that is,

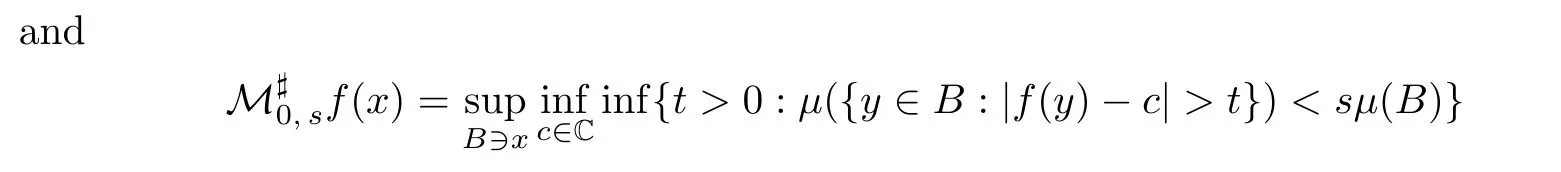
for any locally integrable function f and x∈X.Let M be the Hardy-Littlewood maximal operator and

For a locally integrable function f,de fi ne the Fe ff erman-Stein sharp maximal function M♯f as

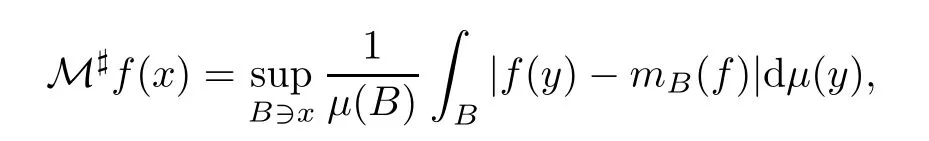
where the supremum is taken over all balls B containing x.For fixed q∈(0,1),let the sharp maximal function be

The commutator of the Hardy-Littlewood maximal operator is de fi ned by

where b∈BMO(X).

The following inequalities will be used in the proof of Theorem 1.1.Let

For α,β∈[0,∞)and any weight w,we have

(see[3]).For any suitable function f,set

Then the following generalization of Hlder’s inequality

holds for any suitable functions f and g;see[7]for details.

2 Some Lemmas

Lemma 2.1Suppose thatµ(X)＜∞,0＜δ＜1,andSis an operator which satis fies the weak type estimate

whereC0is independent offandλ.Then there exists a positive constantCsuch that for anyx∈X,

Proof.Repeating the proof of the Kolmogorov inequality,we see that there exists a positive constant C such that for any

where suppf⊂B.It is easily known that for any x∈X,there exists a ball B satisfying that suppf⊂B and x∈B,such that for any nonnegative integer k,

with C independent of x,f and B.Taking the limit k→∞,we get(2.2).This completes the proof.

Lemma 2.2For anyswith0＜s＜1,there is a positive constantCsuch that for any weightwand any nonnegative functionf,which satis fies thatµ({x∈X:f(x)＞λ})＜∞for anyλ＞0,

The proof of Lemma 2.2 is similar to the proof of Theorem 2.5 in[5],and is omitted. For the setting of Euclidean space,this lemma was proved by Lerner in[6].

Lemma 2.3Under the hypothesis of Theorem1.1,for anyswith0＜s＜1,there exists a constantC＞0such that for any

Proof.Without loss of generality,we may assume thatBy a trivial computation,we see that for any s,q∈(0,1)with q＜s and any locally integrable function f,

3 Proof of Theorem 1.1

We first establish a weighted inequality for the composite operator M♯0,sT∗b.

Theorem 3.1LetTbe a linearL2(X)-bounded operator with kernelKin the sense of(1.1)andb∈BMO(X).Suppose thatKsatis fies the conditions(1.4),(1.5)and(1.7).Then for anyδ＞0,s∈(0,1)andp∈(1,∞),there is a constantC＞0such that for any weightwand

Proof.Notice that for any p∈ (1,∞), δ is an arbitrary positive number.By the Marcinkiewicz interpolation theorem,we see that the proof of Theorem 3.1 can be reduced to prove that for any δ＞0,s∈(0,1)and p∈(1,∞),there is a constant C＞0 such that for any weight w and any

Now we deal with the first term on the right of(3.4).Let

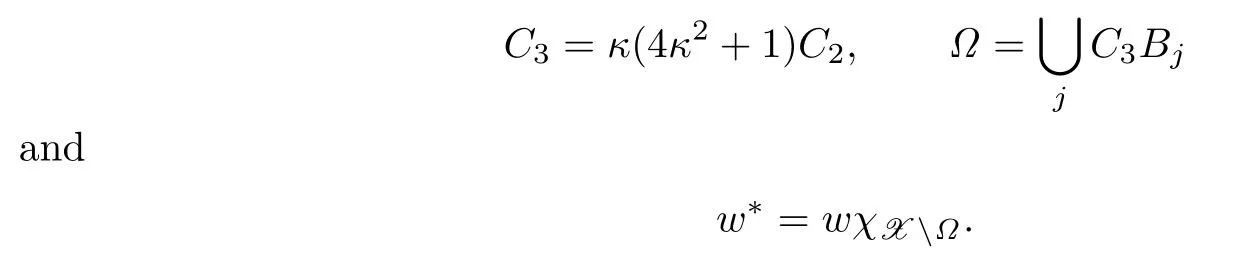
Following an argument similar to the case of Euclidean spaces(see[9],p.159),we can verify that there exists a constant C＞0 depending only on the space X such that for any x∈C2Bj,

(this inequality can be obtained by the same lines to the proof of Lemma 4.3 in[5]with obvious changes)for any weight u and any nonnegative functions g′.Moreover,an application of Hlder inequality via(3.3)gives that

On the other hand,a simple computation states that

Then we deal with the second term on the right of(3.4).Noting that for any s∈(0,1),

where in the second inequality we have invoked the fact that for γ＞0 and any weight w,

(this inequality follows from a similar argument as in the case of Euclidean spaces;see[12], P.651).It suffices to prove that

which implies that

For each fixed x∈XΩ,we de fi ne

where in the third inequality,we have used the fact that for each fixed j,y∈Vjand any positive integer k,a standard argument involving the Hlder inequality and John-Nirenberg inequality yields

On the other hand,because T∗is bounded from L(p+1)/2(X,ML(lgL)(p+1)/2+δw)to L(p+1)/2(X,w)(this conclusion can be obtained from[5]with some obvious change in the proof there),we have

(see[3]);ifµ(X)＜ ∞,we firstly prove thatis an operator satisfying(2.1).For s∈(0,1/2),we have

(these two inequalities can be proven as in the case of Euclidean spaces;see the proofs of Lemma 3.7 in[13]and Theorem 5 in[14]),and so

where in the last inequality we have used Theorem 3.1.Using the same argument as in the proof of Theorem 1.3 in[4],we know thatsatis fies the weak type estimate(2.1).With Lemma 2.1 we can obtain that

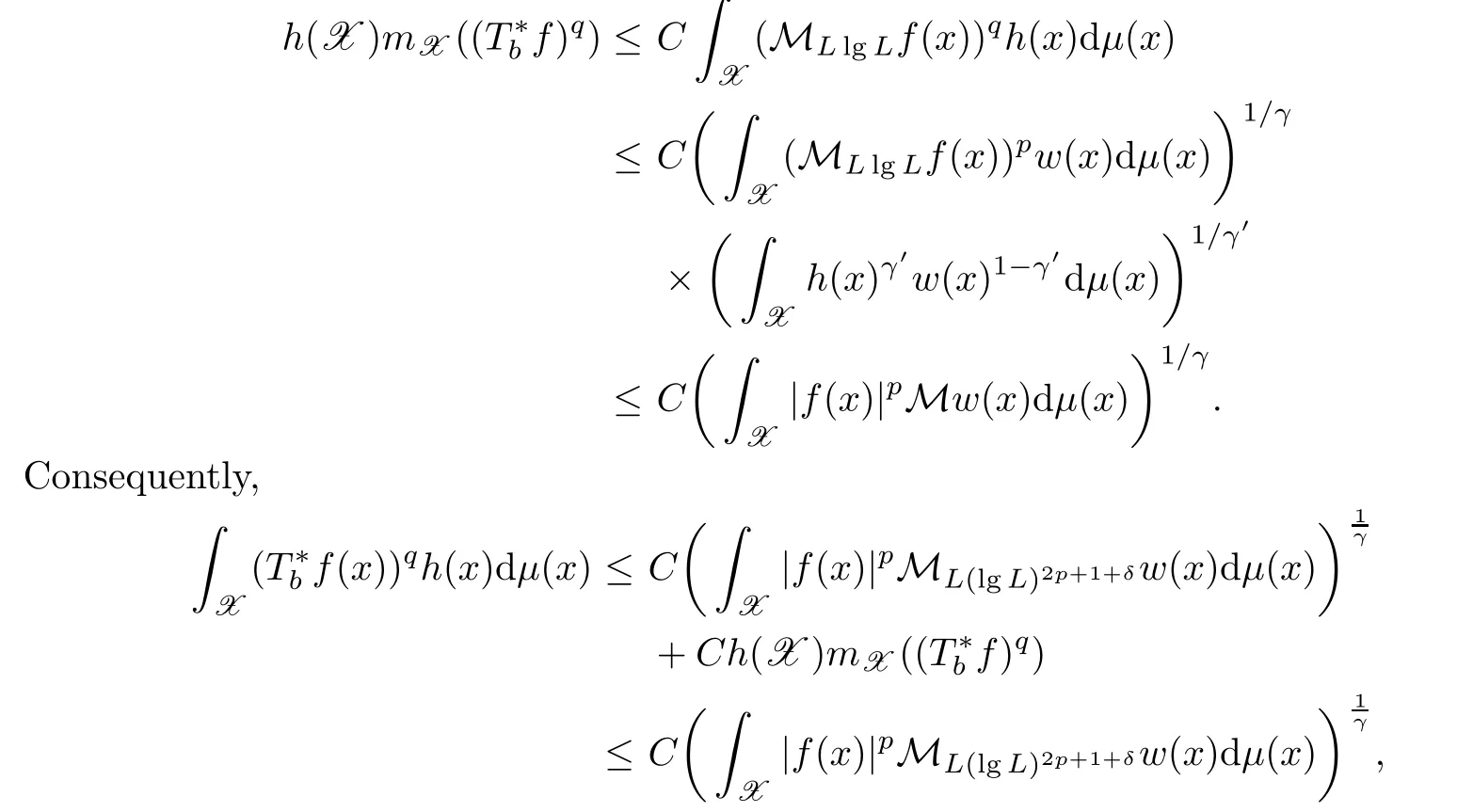
which implies that(1.8)is true.Repeating the argument used in the proof of Theorem 1.3 in[4]we can get(1.9),and then we complete the proof of Theorem 1.1.

[1]Coifman,R.R.and Weiss,G.,Analyse Harmonique Non-commutative Sur Certains Espaces Homogneous,In:Lecture Notes in Math.Vol.242,Springer,Berlin,1971.

[3]Hu,G.and Wang,W.H.,A weighted Lpestimate for the maximal commutator of singular integral operator on spaces of homogeneous type(in Chinese),Acta Math.Sinica,53(2010), to appear.

[4]Hu,G.,Lin,H.B.and Yang,D.C.,Commutators of the Hardy-Littlewood maximal operator with BMO symbols on spaces of homogeneous type,Abstract Appl.Anal.,2008, doi.10.1115/2008/237937.

[5]Hu,G.,Shi,X.L.and Zhang,Q.H.,Weighted norm inequalities for the maximal singular integral operators on spaces of homogeneous type,J.Math.Anal.Appl.,336(2007),1–17.

[6]Lerner,A.K.,Weighted norm inequalities for the local sharp maximal function,J.Fourier Anal.Appl.,10(2004),465–474.

[7]Rao,M.M.and Ren,Z.D.,Theory of Orlicz Spaces,Marcel Dekker,Inc.,New York,1991.

[8]Aimar,H.,Singular integrals and approximate identities on spaces of homogeneous type,Trans. Amer.Math.Soc.,292(1985),135–153.

[10]Hu,G.E.,Yang,D.C.and Yang,D.Y.,Boundedness of maximal singular integral operators on spaces of homogeneous type and its applications,J.Math.Soc.Japan,59(2007),323–349.

[11]Pradolini,G.and Salinas,O.,Maximal operators on spaces of homogeneous type,Proc.Amer. Math.Soc.,132(2003),435–441.

[12]Hu,G.and Li,D.F.,A Cotlar type inequality for the multilinear singular integral operators and its applications,J.Math.Anal.Appl.,290(2004),639–653.

[14]Fe ff erman,C.and Stein,E.M.,Hpspaces of several variables,Acta Math.,129(1972),137–193.

Communicated by Ji You-qing

42B20,47A99

A

1674-5647(2010)01-0053-14

date:Sept.9,2008.