Star-shaped differentiable Functions and Star-shaped differentials∗

PAN SHAO-RONG,ZHANG HONG-WEIAND ZHANG LI-WEI

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian,116024)

(2.School of Mathematical Sciences,Harbin Normal University,Harbin,150080)

Star-shaped differentiable Functions and Star-shaped differentials∗

PAN SHAO-RONG1,2,ZHANG HONG-WEI1AND ZHANG LI-WEI1

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian,116024)

(2.School of Mathematical Sciences,Harbin Normal University,Harbin,150080)

Based on the isomorphism between the space of star-shaped sets and the space of continuous positively homogeneous real-valued functions,the star-shaped differential of a directionally differentiable function is de fi ned.Formulas for star-shaped differential of a pointwise maximum and a pointwise minimum of a finite number of directionally differentiable functions,and a composite of two directionally differentiable functions are derived.Furthermore,the mean-value theorem for a directionally differentiable function is demonstrated.

The space of star-shaped sets,gauge function,isometrical isomorphism, directionally differentiable function,star-shaped differential,mean-value theorem

1 Introduction

In 1950s and 1960s Fenchel and Rockafellar[1]investigated differential theory and optimization theory for nonsmooth convex functions.A convex function is directionally differentiable and its subdifferential is a convex set.In 1970s Clarke[2]made contributions to the differential and optimization theory for Lipschitz continuous functions.The generalized subdifferential for a Lipschitz function is a convex set,but the set of generalized directional derivatives for Lipschitz continuous functions is not a linear space.In 1969,Pshenichyi[3]suggested the concept of quasidifferentiability where the directional derivative is a sublinear function.But the class of quasidifferentiable functions in the sense of Pshenichnyi is insuffi cient to describe many important situations;for instance,it cannot include the so-called D.C.functions.In 1970s,Demyanov,Rubinov and Polyakova extended the concept of quasidifferentiable functions in the sense of Pshenichnyi by introducing a new de fi nition,whichensures many good properties about arithmetic operations of quasidifferentiable functions in the new sense(see[4]and[5]).A quasidifferentiable function in the sense of Demyanov and Rubinov is directionally differentiable and its directional derivative is representable as a di ff erence of two convex functions with the differential as a pair of convex compact sets.The class of quasidifferentiable functions,in the sense of Demyanov and Rubinov,have a very wide practical applied background,such as problems for storages and problems for optimum layout of circuits.

Recently,noticing that many functions appearing in bilevel programs are a new class of important directionally differentiable functions,Zhanget al.[6]proposed the concept of generalized quasidifferentiable functions,and Zhanget al.[7]explored the optimality conditions for nondifferentiable optimization problems of generalized quasidifferentiable functions.But for a general directionally differentiable function without any structures,there is no suitable de fi ntion for its differential.Observing that if the directionally derivative is a positively homogeneous continuous function in direction,then it can be represented as a di ff erence of two nonnegative positively homogeneous continuous functions,we can express the directional derivative as the di ff erence of two gauge functions of star-shaped sets.A directionally differentiable function whose directional derivatives is continuous in direction is de fi ned as a star-shaped differentiable function.A star-shaped differential of a star-shaped differentiable function is a pair of star-shaped sets,but not a pair of convex compact sets.We can verify that any quasidifferentiable function in the sense of Demyanov and Rubinov is star-shaped differentiable.

In this paper,we first present some preliminaries about the space of star-shaped sets. Secondly,we give the concept of star-shaped differential and verify arithmetic operations of star-shaped differentials,and derive formulas for star-shaped differentials of a pointwise maximum and of a pointwise minimum of a finite number of directionally differentiable functions,and a composite of two directionally differentiable functions.Finally,we demonstrate the mean-value theorem for a star-shaped differentiable function.

2 Preliminaries

In this section we recall some results about the space of star-shaped sets and the space of positively homogeneous continuous functions(see[8]).

De fi nition 2.1[9]A closed subsetAofRnis called a star-shaped set if it contains the origin as an interior point and every ray

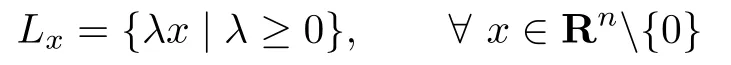
does not intersect the boundary ofAmore than once.

De fi ne

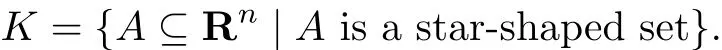
We introduce a partial order in K2,denoted by,in the sense that for(Ai,Bi)∈K2, i=1,2,

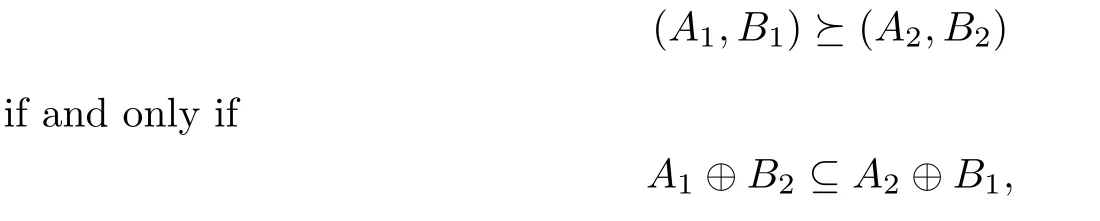
where⊕(called inverse sum)is de fi ned by

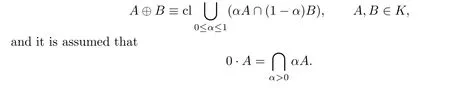
An equivalence relation,denoted by～,is deduced from this partial order,i.e.,for(Ai,Bi)∈K2,i=1,2,

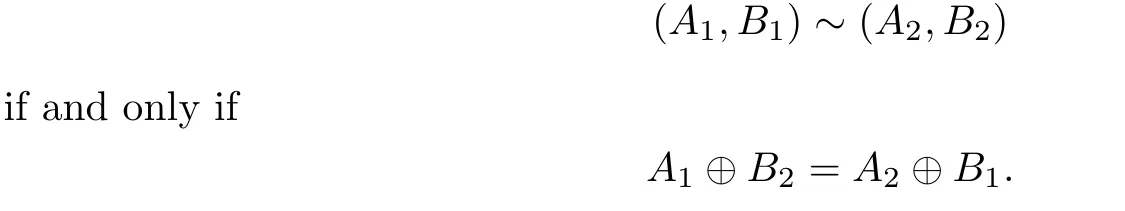
Let K1=K2/～and de fi ne the inverse sum⊕and inverse scalar multiplication⊙in K1as follows:

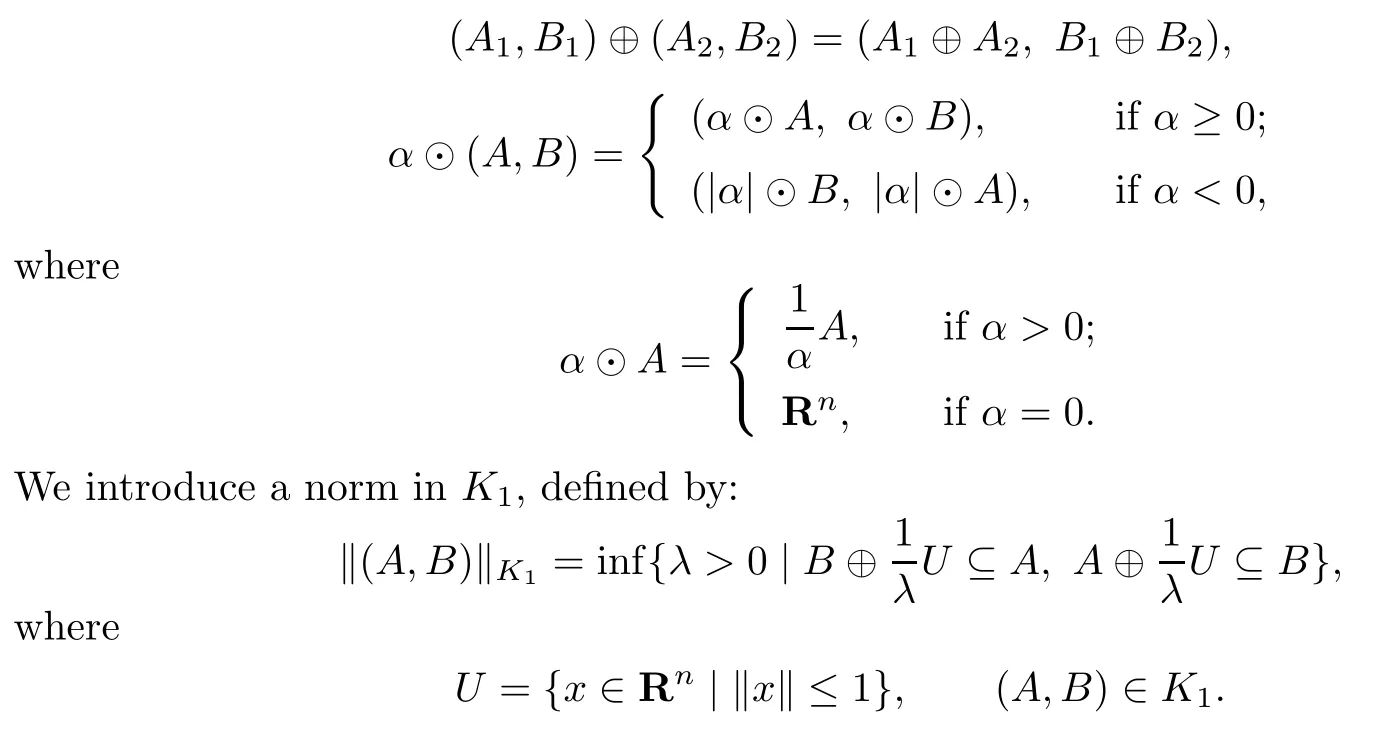
Define

H={σ:Rn→R|σ is a nonnegative positively homogeneous and continuous function}.

A partial order in H2,denoted by,is de fi ned by

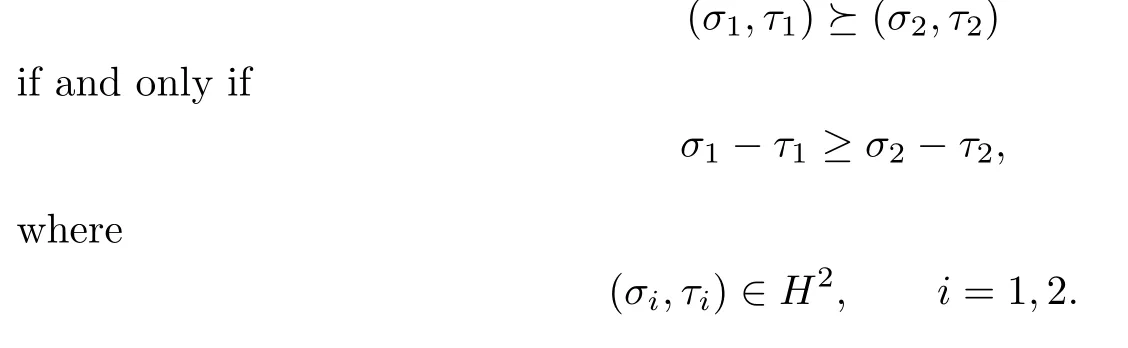
An equivalence relation,denoted by～,is deduced from this partial order,i.e.,

De fi ne H1=H2/～and introduce addition operation and scalar multiplication operation in H1as follows:

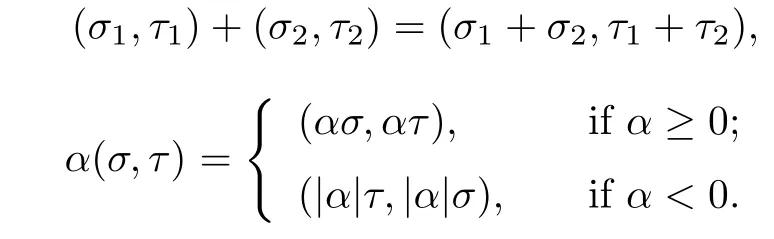
De fi ned a norm in H1by

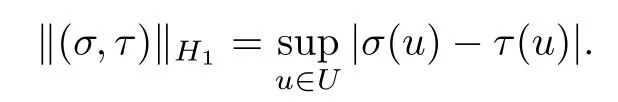
Let A⊆Rn,0∈intA.The function φ(A):Rn→Rde fi ned by

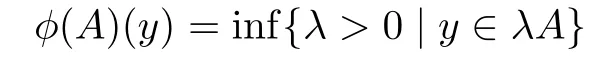
is called the gauge(or the Minkowski gauge function)of a set A.If A is convex then the gauge coincides with the gauge function in the sense of convex analysis.The following lemma plays an important role in studying the isomorphism between the space of star-shaped sets and the space of positively homogeneous continuous functions.

Lemma 2.1[9]Letψ:Rn→R.The following statements are equivalent:

(i)the functionalψis positively homogeneous,nonnegative and continuous;

(ii)ψcoincides with the gauge of a star-shaped set Ω,where Ω={x|ψ(x)≤1}.Theorem 2.1The mappingTΦ:K1→ Cp,his a linear isometricallyRieszisomorphism.

3 Star-shaped differentials

are convex compact sets.Hence,f is quasidifferentiable at x in the sense of Demyanov and Rubinov.On the other hand,if f is quasidifferentiable at x in the sense of Demyanov and Rubinov,then f is star-shaped differentiable at x,and

are star-shaped convex sets.Thus all quasidifferentiable functions are star-shaped differentiable.

Example 3.1[10]Consider the function

The function f is directionally differentiable at¯x=(0,0),and for every d∈R2,we have

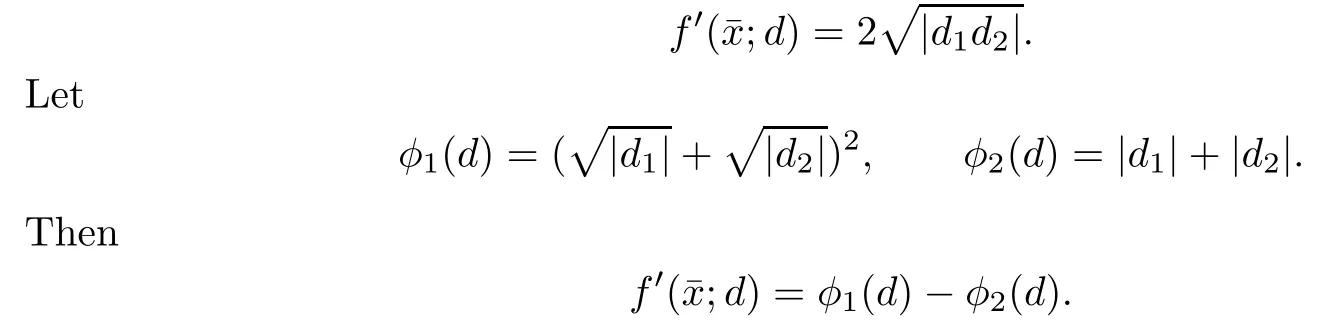
It is clear that φ1(d)and φ2(d)are nonnegative positively homogeneous continuous functions in d.From Lemma 2.1,we obtain

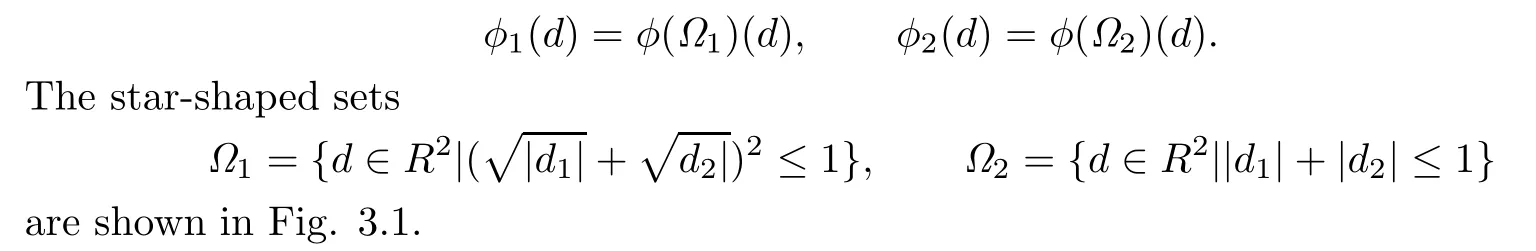
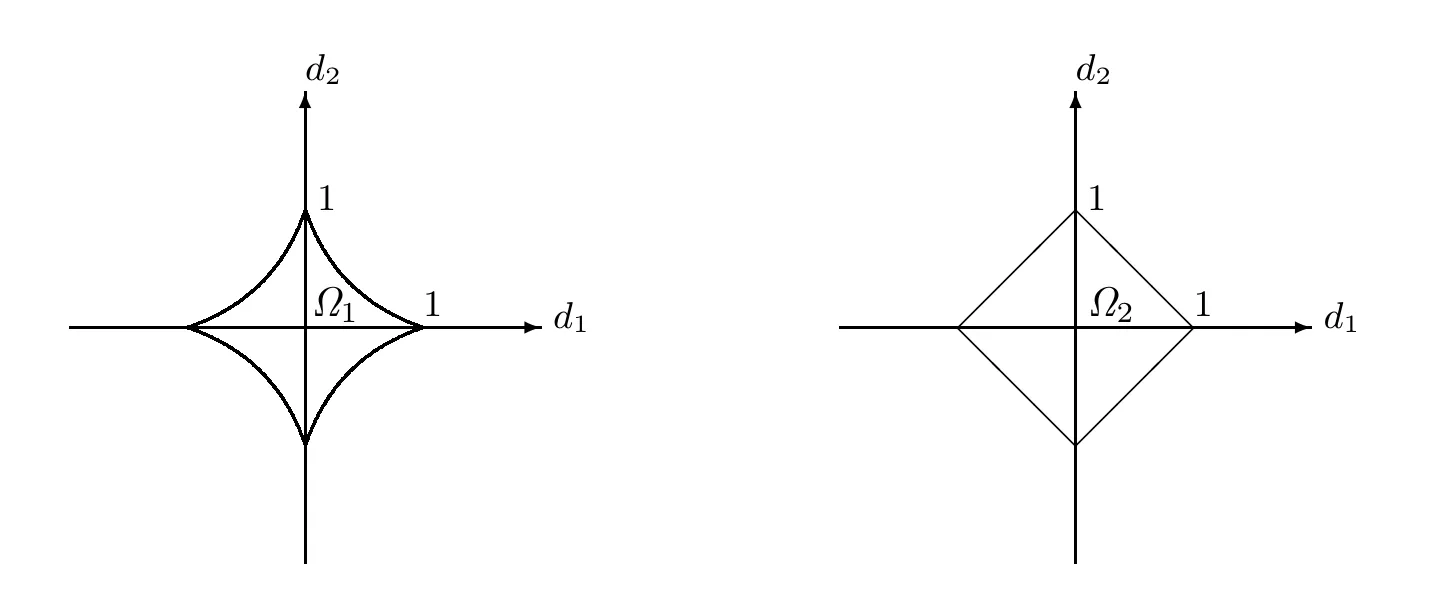
Fig.3.1

Thus,

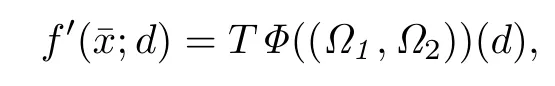
where(Ω1,Ω2)∈K1.Therefore,f is star-shaped differentiable at=(0,0).But f is not Lipschitz continuous around,so,f is not quasidifferentiable atin the sense of Demyanov and Rubinov.

The following conclusion is obvious.

Theorem 3.1Letf:Rn→Rbe directional differentiable atx∈Rn.The functionfis star-shaped differentiable atxif and only iff′(x;d)is positively homogeneous continuous ind∈Rn.

Lemma 3.1(Arithmetic operations of star-shaped differentials)

We can prove(ii),(iii)and(iv)in a similar way,and we omit the details here.The proof is completed.

In the following,formulas for star-shaped differential of a pointwise maximum,a pointwise minimum of a finite number of directionally differentiable functions,and a composite of two directionally differentiable functions are derived.De fi ne

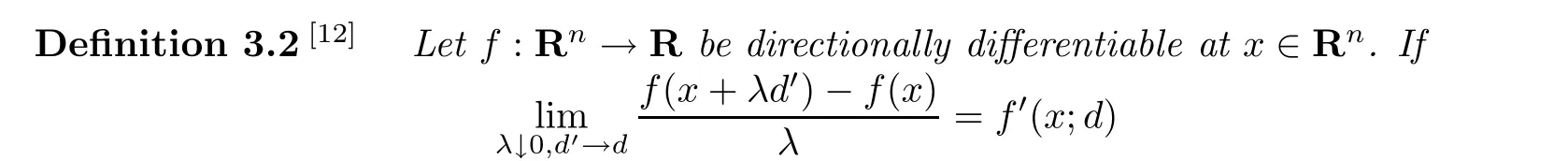
for any vectord∈Rn,we say thatfis directionally differentiable atx∈Rnin the Hadamard sense.

It follows from Proposition 2.46 of[12]that if f is directionally differentiable at x∈Rnin the Hadamard sense,then f′(x;·)is continuous,so f is star-shaped differentiable at x.Theorem 3.2Letfi:Rn→R(i=1,2,···,m)be star-shaped differentiable atx0∈Rnandψbe directionally differentiable at

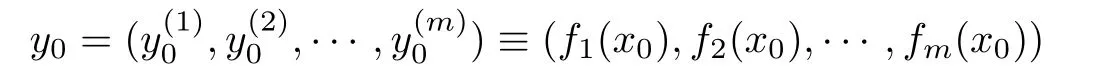
in the Hadamard sense.ThenFis star-shaped differentiable atx0.

Proof.By Proposition 2.47 of[12],we have that F is directionally differentiable at x0and for any d∈Rn,

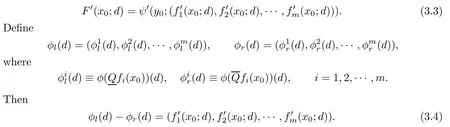
Again,since ψ is star-shaped differentiable at y0,combining(3.3)with(3.4),we obtain

and F is star-shaped differentiable at x0with QF(x0)=(Ω1,Ω2)∈K1,whereΩ1,Ω2are given by(3.5)and(3.6).

4 An Mean-value Theorem

Consider a univalent function φ:R→Rand let φ be a star-shaped differentiable function on R.Since a star-shaped set in the univariate space R is a convex set,the mean-value theorem for a univalent quasidifferentiable function,in the sense of Demyanov and Rubinov, applies for a univalent directionally differentiable function.

[1]Rockfellar,R.T.,Convex Analysis,Princeton University Press,Princeton,New Jersey,1970.

[2]Clarke,F.H.,Genaralized gradients and applications,Trans.Amer.Math.Soc.,205(1975), 247–262.

[3]Pschenichnyi,B.N.,Necessary Conditions for an Extremum,Marcel Dekker,New York,1971.

[4]Demyanov,V.F.,Polyakova,L.N.and Rubinov,A.M.,On one generalization of the concept of subdifferential,Abstracts of Reports in All Union Conference on Dynamic Control,Sverdlovsk, 1979,pp.79–84.

[5]Demyanov,V.F.and Rubinov,A.M.,On quasidifferentiable functionals,Dokl.Akad.Nauk UzSSR,250(1980),21–25.

[6]Zhang,H.W.,Zhang,L.W.and Xia,Z.Q.,Calculus of generalized quasi-differentiable functions I:some results on the space of pairs of convex-set collections,Northeast.Math. J.,19(2003),75–85.

[7]Zhang,H.W.,Zhang,L.W.,Xia,Z.Q.and Song,C.L.,Optimality conditions for generalized quasidifferentiable optimization problems with inequality constraints,J.Dalian Univ.Tech., 46(2006),299–301.

[8]Zhang,H.W.,Pan,S.R.and Zhang,L.W.,The space of star-shaped sets and its applications, submitted.

[9]Rubinov,A.M.and Yagubov,A.A.,The space of star-shaped sets and its applications in nonsmooth optimization,Math.Program.Study,29(1986),176–202.

[10]Demyanov,V.F.and Rubinov,A.M.,Quasidifferentiablity and Related Topics,Kluwer Acsdemic Publishers,Dordrecht,2000.

[11]Demyanov,V.F.and Rubinov,A.M.,Constructive Nonsmooth Analysis,Peter Lang,Frankfurt am Main,New York,1995.

[12]Bonnans,J.F.and Shapiro,A.,Perturbation Analysis of Optimization Problems,Springer, New York,2000.

Communicated by Yin Jing-xue

90C30,90C90

A

1674-5647(2010)01-0041-12

date:June 17,2008.

The NSF(10771026)of China.