Asymptotic Distribution of a Kind of Dirichlet Distribution∗

CHEN FEIAND SONG LI-XIN

(1.Science College,Changchun University,Changchun,130022)

(2.Mathematical College,Jilin Normal University,Siping,Jilin,136000)

Asymptotic Distribution of a Kind of Dirichlet Distribution∗

CHEN FEI1AND SONG LI-XIN2

(1.Science College,Changchun University,Changchun,130022)

(2.Mathematical College,Jilin Normal University,Siping,Jilin,136000)

The Dirichlet distribution that we are concerned with in this paper is very special,in which all parameters are different from each other.We prove that the asymptotic distribution of this kind of Dirichlet distributions is a normal distribution by using the central limit theorem and Slutsky theorem.

Dirichlet distribution,asymptotic distribution,normal distribution

Document code:A

1 Introduction

The Dirichlet distribution is a common multivariate distribution.It not only plays a very important role in modern non-parameter statistics,but also serves as the conjugate priori distribution of the multinomial distribution which is wildly used in Bayes statistics.As we know,the limit distribution of the Beta distribution is a normal distribution(see[1]),and the Dirichlet distribution is the multivariate form of the Beta distribution(see[2]).So it is very important to investigate the asymptotic distribution of the Dirichlet distribution. For the Dirichlet distribution in which all parameters are the same,we have obtained an important conclusion(see[3]).But the Dirichlet distribution that we are concerned with in this paper is very special,in which all parameters are different from each other.We prove that the asymptotic distribution of this kind of Dirichlet distributions is still a normal distribution by using the central limit theorem and Slutsky theorem.

2 Main Result

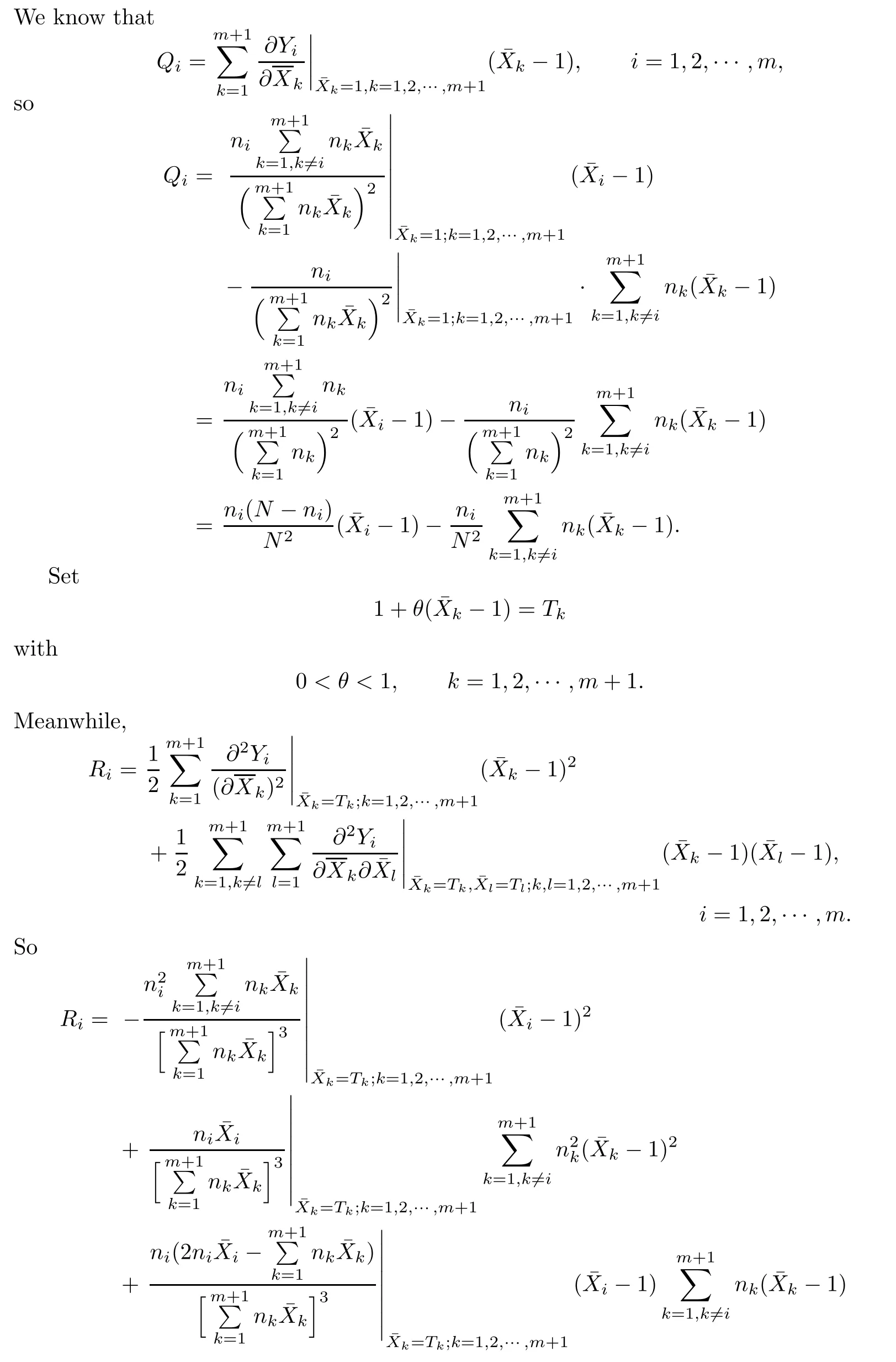
For any real number t and j=1,2,···,nt,BtWtjis of i.i.d.By Lemma 2.1(the multivariate central limit theorem)we obtain that

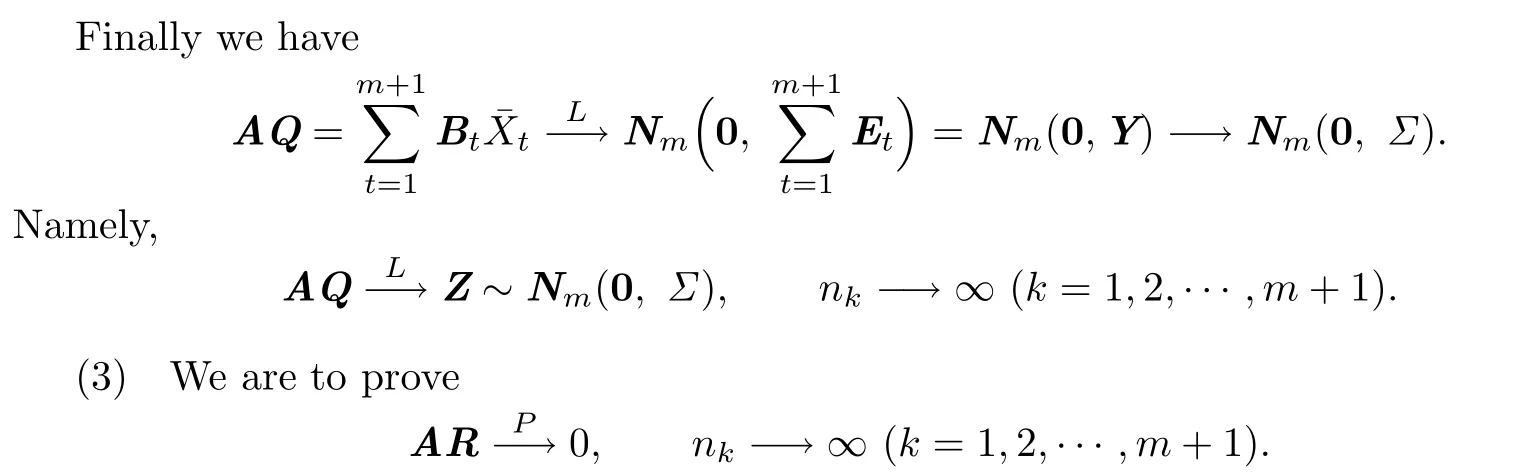
Noting that the matrix A and the vector R are shown before,by means of an easy calculation we get

in which the i-th component of AR is

Then by repeated use of the Slutsky theorem we are to prove that each of S1,S2,S3,S4converges to 0 in probability.

[1]Li Ze-hui and Li Xiao-hu,Exercises Course of Mathematical Statistics,Lanzhou University Press,Lanzhou,1995.

[2]Zhang Yao-ting and Fang Kai-tai,Introduction of Multivariate Statistical Analysis,Science Press,Beijing,2003,pp.364–365.

[3]Song Li-xin,Chen Fei and Li Han,Asymptotic distribution of a kind of Dirichlet distribution,J.Jilin Univ.(Science Edition),45(5)(2007),775–778.

[4]Zhang Yao-ting,The Determinable Data’s Statistic Analysis,Guangxi Normal University Press, Naning,1991.

[5]Chen Fei and Song Li-xin,Spread about Theorem,Jilin Normal University Journal,26(2)(2005), 41–42.

[6]Mao Shi-song,Wang Jing-long and Pu Xiao-long,Senior Mathematical Statistics,Higher Education Press,Beijing,1998.

[7]Fang Kai-tai and Xu Jian-lun,Statistic Distribution,Science Press,Beijing,1987.

Communicated by Wang De-hui

65M02,65N15,65R43

O241.81

1674-5647(2010)01-0017-10

date:Oct.16,2008.

Plan Project of Department of Education Science and Technology of Jilin Province, No.152[2007].