应变Si PMOSFET电流特性研究*

胡辉勇，崔晓英 ，张鹤鸣宋建军戴显英宣荣喜

1.西安电子科技大学微电子学院，宽禁带半导体材料与器件重点实验室，西安 710071；

2.中国电子科技集团第五研究所分析中心，广州 510610

随着硅MOSFETs尺寸的减小，其性能可以得到显著的提高。然而，随着每一代技术的产生，单纯靠减小尺寸的方法来提高器件性能变得越来越难。因此，要研究新型的器件结构和材料来推进其性能的发展。应变Si(SSi)科技是一项快速崛起的技术，它提供了比体Si器件要优越得多的性能并拥有良好的工艺兼容性，因此应变Si器件受到越来越高的重视。

应变Si中的电子迁移率显著的高于体Si，并且应变Si已经被用于制造高性能的应变Si NMOSFET器件，同样的，对于应变Si中有高的空穴迁移率这一点引起了人们制造应变Si PMOSFET的兴趣。Si在弛豫的SiGe层上生长产生张应变，轻空穴带上升，重空穴带降低，从而大大提高了低场迁移率。有资料显示用MBE可以生长高质量的应变Si层，可以制造出高性能的应变Si PMOSFET[1]，因此对其研究是有意义的。近年来对应变Si MOSFET的研究多着重于应变材料中迁移率的改善和具体器件的制造，对其电学特性模型的研究相对较少；另外对应变Si PMOSFET的研究明显少于应变Si NMOSFET[2-3]。本文研究并讨论了应变Si PMOSFET的电学特性，在分析器件物理结构的基础上，推导出解析的阈值电压，和电流电压特性等模型，并给出了Matlab的模拟结果。

1 I-V特性

应变Si PMOSFET的结构如图1所示。由于价带的不连续，在应变Si PMOSFET中形成表面沟道的同时，在SiGe/Si界面SiGe一侧会产生一个寄生的掩埋沟道，从图2的能带结构图中可以看到Si/SiGe界面有一个价带差，因此除了表面沟道还会形成一个寄生的掩埋沟道。然而，使用渐变的Si/SiGe界面可以减小价带差，从而消除寄生沟道。这样，表面沟道中的空穴浓度就会增加。

图1 应变Si PMOS结构示意图

图2 应变Si PMOS能带示意图

图1中在弛豫SiGe层上生长的Si产生张应变，轻空穴带升高，重空穴带降低，使空穴传导有效质量降低，从而提高了应变Si PMOSTETs中的空穴迁移率。表面Si沟道层应变的程度与SiGe层表面Ge组分x相关， Ge组分越高，应变程度也越大，禁带宽度越窄，迁移率越高。

由于张应变产生的导带和价带分裂，以及应变Si与弛豫SiGe之间禁带宽度、亲和势、介电常数的不同，使得导带和价带产生不连续。其禁带宽度[4]及导带和价带的偏移量[5]分别为(x为Ge组分)：

导带和价带的较大偏移量使得应变Si既适合于做NMOSFET，又适合于做PMOSFET。

应变Si的本征载流子浓度可以表示为：niSSi=，应变Si的导带有效状态密度Nc和价带有效状态密度Nv可由下式求出：

式中mn* =0.196 m0为导带电子有效质量；mp* =0.16 m0为价带空穴有效质量，比Si空穴有效质量0.59 m0要小得多。则可算出T=300 K时应变Si的本征载流子浓度：

在应变Si MOSFETs中，通常Si沟道区比较薄，并且比耗尽层宽度小。假设漏源偏压不大，并且忽略短沟道效应，在垂直于表面方向做一维分析，并对泊松方程进行求解。首先可以列出泊松方程为：

xdth为最大耗尽层厚度， tSi和tox分别为应变Si和栅氧化层的厚度。εox、εSi和εSiGe分别为氧化层、应变Si和弛豫SiGe的介电常数。沟道开始强反型时阈电势可以由下式解得：

阈电势可以表示为：

NSiGe为衬底掺杂浓度；价带偏移量ΔEv=0.74x-0.53x2；niSS为本征载流子浓度。

在应变 Si沟道开启时的 SiGe耗尽层宽度xdth为：

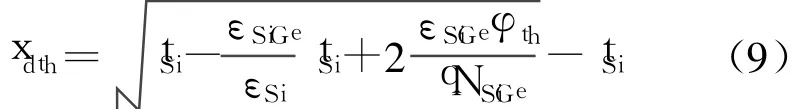
设VFB为平带电压， Cox为栅氧化层的电容，那么阈值电压Vth可以表示为：

在MOSFET器件中，电场对器件的沟道迁移率有非常大的影响，栅介质层越薄，掺杂水平越高，纵向电场就越高，这样的高电场将会极大的降低器件的性能。因此在模型中采用有效迁移率来表征，有效迁移率随着电场的改变而改变。本文讨论在有栅压VGS的情况下，应变Si沟道空穴高场迁移率与Ge组分及栅压的关系。沟道迁移率[5]由三种机制的迁移率组成，表达式如下：

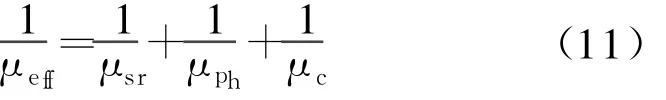
声子迁移率表示为：

其中：

Qi为应变Si沟道反型层电荷， Qb为SiGe沟道耗尽区电荷[6]。

参数：

表面粗糙度散射迁移率表示为：

其中：

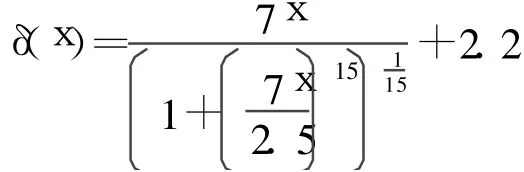
库仑散射(电离杂质散射)迁移率表示为：

其中：C为常数：45.45×10-9V◦s/cm， NS为应变Si沟道平均空穴浓度， NSi同上。由面电荷密度QS=qNStSi，电位移矢量D=εSiEEFF可推出：

那么电流电压公式可以表示为：

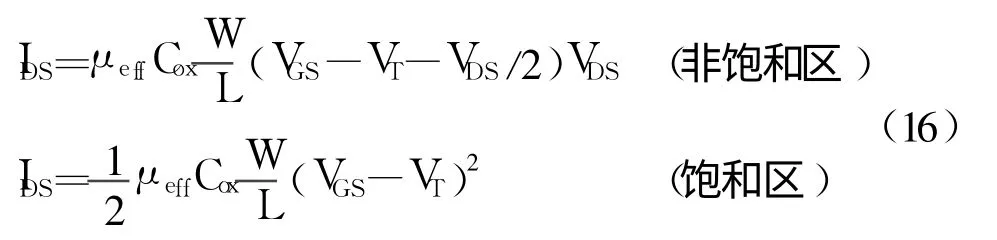
2 模拟结果与讨论

应变Si迁移率与Ge组分的关系如图3 所示，模拟中采用的器件结构参数为：栅氧化层厚度为10 nm，应变Si层厚度为13.5 nm，掺杂为1016cm-3，SiGe层掺杂为1018cm-3。模拟可得在沟道开启后，空穴迁移率随Ge组分及栅压变化的关系。

图3 应变Si迁移率与Ge组分的关系

由图3可知：迁移率随着Ge组分而增加。这是由于在弛豫SiGe上生长Si产生张应变，升高了轻空穴带，降低了重空穴带，大大减小了谷间散射，其有效质量变小，从而提高了迁移率。当Ge组分达到25%左右时，迁移率达到饱和，不再增加。这种现象可以通过随着Ge摩尔组分的增加使其分裂的子能带数目的变化来得到解释。 Ge组分增加应变增大，使得能带分离加剧，未被填充的子能带相对于被填充的子能带数目增加，载流子被局限在少数的几个填充的子带内而不会跳越进其他更多的子带，也就是迁移率会逐渐饱和等于那几个填充满的子带内的载流子迁移率[7]。

与传统Si NMOSFET的电流电压特性曲线相似， IDS随VDS和VGS的增加而上升。在VDS=VDsat=VGS-VTH时， IDS达到饱和。沟道长度为90 nm，从图4中可以看到，模拟所得的结果与K.Rim， J.Chu等人[6]得到的曲线(VGS=-1.5 V时， 漏电流为420 μA/μm)是非常符合的。饱和栅跨导为：

图4 应变SiPMOSFET的I-V特性

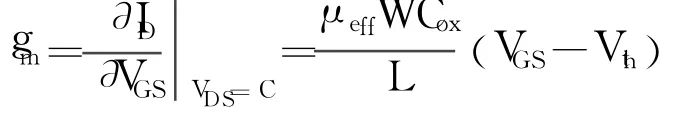
应变Si PMOSFET的饱和栅跨导与栅压及Ge组分的关系曲线如图5所示，结构参数为：栅氧化层厚度为10 nm，应变Si层厚度为13.5 nm，掺杂为1016cm-3， SiGe层 掺 杂 为 1018cm-3， 沟 道 长 度 为90 nm。

图5 应变Si PMOSFET的饱和栅跨导

在图5中：饱和栅跨导随着栅压的增加而上升，随着Ge组分的增加而上升，在栅压较大时，变化趋势减小。这是由于Ge组分的增加，将使阈值电压减小，载流子有效迁移率上升，因此栅跨导将升高。而电子有效迁移率μeff将随VGS的上升而降低。

3 结论

本文推导出了应变Si PMOSFET的解析的阈值电压模型，以及电流电压特性，和跨导等电学特性参数模型，这些参数与Ge组分以及掺杂浓度有着密切的关系。最后，用MATLAB软件对各项电学参数进行了模拟，取得了非常好的结果。此模型作为对PMOSFET进行模拟和电学参数的计算是非常有用的工具。

[ 1] Zhang Weim in， Fossum Jerry G.On the Threshold Voltage of Strained-Si-SiGe MOSFETs[ J] .IEEE Transactions on Electron Devices， 2005， 52(2)：263.

[ 2]Olsen SH， Kwa K SK， Driscoll LS， et al.Design， Fabrication and Characterisation of Strained Si-SiGe MOS Transistors[ J].IEE Process-Circuits Devices System， 2004， 151(10)：431.

[ 3]Jung Jongwan， Lee Mingjoo L， Yu Shaofeng， et al.Implementation of Both High-Hole and Electron Mobility in Strained Si/Strained Si1-yGeyon Relaxed Si1-xGex(x＜y)Virtual Substrate.IEEE Electron Device Letters， 2003， 24(7)：460.

[ 4]Goo Jung-Suk， QiXiang， YayoiTakamura， et al.Band Offset Induced Threshold Variation in Strained-Si nMOSFETs[ J] .IEEE Electron Device Letter， 2003， 24(9)：568.

[ 5]Anthony Kang， Jason Moss， Jonathan Torok.Strained Silicon[Z] .Rose-Hulman Institute of Technology， 2003， 21：553-3.

[ 6]Lochtefeld A， Djomehri IJ， Samudra G， et al.New Insights Into Carrier Transport in N-MOSFETs[ J] .IBM Journal of Research and Development， 2002， 46(2-3)：374；

[ 7]Roldan JB， Gam iz F， Cartujo-CassinelloP， etal.Strained-Si on Si1-xGexMOSFETMobility Model[ J] .IEEE Transactions on Electron Devices， 2003， 50(5)：1408.

[ 8]Rim K， Chu J， Chen H， etal.Characteristicsand Device Design of Sub-100 nm Strained Si N-and PMOSFETs[C] //IEEE Symposium On VLSI Technology Digest of Technical Papers， 2002：98-99.

[ 9]Michelakis K， Vilches A， Papavassiliou C， et al.Average Drift Mobility and Apparent Sheet-Electron Density Profiles in Strained-Si-SiGe Buried-Channel Depletion-Mode n-MOSFETs[ J] .IEEE Transaction on Electron Devices， 2004， 51(8)：1309.

[ 10] Karthik Chandrasekaran.Computational Investigation of Novel Device Structures and Concepts[ D] .School of Electrical and Electronic Engineering， Nanyang Technological University， Singapore May， 2003.

[ 11] Deepak K N， Goto K Yutani A， et al.High-Mobiliy Strained-Si PMOSFET's[ J] .IEEE Transactions on Electron Devices， 1996，43(10)：1709.